Certified Symmetry and Dominance Breaking for Combinatorial Optimisation

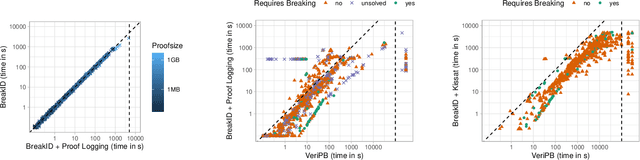
Symmetry and dominance breaking can be crucial for solving hard combinatorial search and optimisation problems, but the correctness of these techniques sometimes relies on subtle arguments. For this reason, it is desirable to produce efficient, machine-verifiable certificates that solutions have been computed correctly. Building on the cutting planes proof system, we develop a certification method for optimisation problems in which symmetry and dominance breaking are easily expressible. Our experimental evaluation demonstrates that we can efficiently verify fully general symmetry breaking in Boolean satisfiability (SAT) solving, thus providing, for the first time, a unified method to certify a range of advanced SAT techniques that also includes XOR and cardinality reasoning. In addition, we apply our method to maximum clique solving and constraint programming as a proof of concept that the approach applies to a wider range of combinatorial problems.

A Review of Literature on Parallel Constraint Solving

As multicore computing is now standard, it seems irresponsible for constraints researchers to ignore the implications of it. Researchers need to address a number of issues to exploit parallelism, such as: investigating which constraint algorithms are amenable to parallelisation; whether to use shared memory or distributed computation; whether to use static or dynamic decomposition; and how to best exploit portfolios and cooperating search. We review the literature, and see that we can sometimes do quite well, some of the time, on some instances, but we are far from a general solution. Yet there seems to be little overall guidance that can be given on how best to exploit multicore computers to speed up constraint solving. We hope at least that this survey will provide useful pointers to future researchers wishing to correct this situation. Under consideration in Theory and Practice of Logic Programming (TPLP).