A Review of Literature on Parallel Constraint Solving

As multicore computing is now standard, it seems irresponsible for constraints researchers to ignore the implications of it. Researchers need to address a number of issues to exploit parallelism, such as: investigating which constraint algorithms are amenable to parallelisation; whether to use shared memory or distributed computation; whether to use static or dynamic decomposition; and how to best exploit portfolios and cooperating search. We review the literature, and see that we can sometimes do quite well, some of the time, on some instances, but we are far from a general solution. Yet there seems to be little overall guidance that can be given on how best to exploit multicore computers to speed up constraint solving. We hope at least that this survey will provide useful pointers to future researchers wishing to correct this situation. Under consideration in Theory and Practice of Logic Programming (TPLP).

An n-ary Constraint for the Stable Marriage Problem

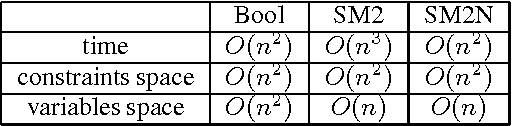
We present an n-ary constraint for the stable marriage problem. This constraint acts between two sets of integer variables where the domains of those variables represent preferences. Our constraint enforces stability and disallows bigamy. For a stable marriage instance with $n$ men and $n$ women we require only one of these constraints, and the complexity of enforcing arc-consistency is $O(n^2)$ which is optimal in the size of input. Our computational studies show that our n-ary constraint is significantly faster and more space efficient than the encodings presented in \cite{cp01}. We also introduce a new problem to the constraint community, the sex-equal stable marriage problem.