From Stories to Cities to Games: A Qualitative Evaluation of Behaviour Planning

The primary objective of a diverse planning approach is to generate a set of plans that are distinct from one another. Such an approach is applied in a variety of real-world domains, including risk management, automated stream data analysis, and malware detection. More recently, a novel diverse planning paradigm, referred to as behaviour planning, has been proposed. This approach extends earlier methods by explicitly incorporating a diversity model into the planning process and supporting multiple planning categories. In this paper, we demonstrate the usefulness of behaviour planning in real-world settings by presenting three case studies. The first case study focuses on storytelling, the second addresses urban planning, and the third examines game evaluation.

Faster Symmetry Breaking Constraints for Abstract Structures

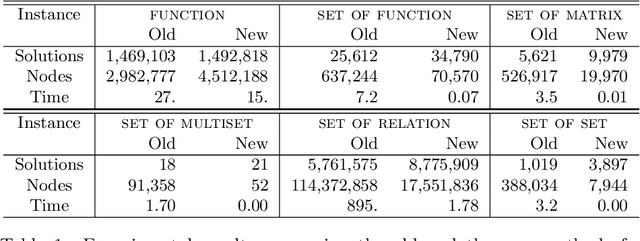
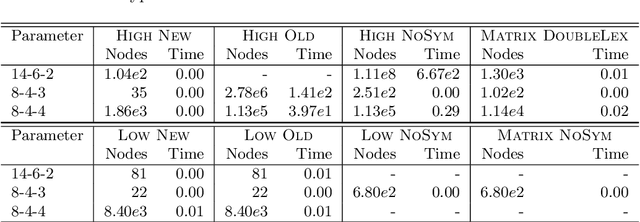
In constraint programming and related paradigms, a modeller specifies their problem in a modelling language for a solver to search and return its solution(s). Using high-level modelling languages such as Essence, a modeller may express their problems in terms of abstract structures. These are structures not natively supported by the solvers, and so they have to be transformed into or represented as other structures before solving. For example, nested sets are abstract structures, and they can be represented as matrices in constraint solvers. Many problems contain symmetries and one very common and highly successful technique used in constraint programming is to "break" symmetries, to avoid searching for symmetric solutions. This can speed up the solving process by many orders of magnitude. Most of these symmetry-breaking techniques involve placing some kind of ordering for the variables of the problem, and picking a particular member under the symmetries, usually the smallest. Unfortunately, applying this technique to abstract variables produces a very large number of complex constraints that perform poorly in practice. In this paper, we demonstrate a new incomplete method of breaking the symmetries of abstract structures by better exploiting their representations. We apply the method in breaking the symmetries arising from indistinguishable objects, a commonly occurring type of symmetry, and show that our method is faster than the previous methods proposed in (Akgün et al. 2025).

Breaking the Symmetries of Indistinguishable Objects

Indistinguishable objects often occur when modelling problems in constraint programming, as well as in other related paradigms. They occur when objects can be viewed as being drawn from a set of unlabelled objects, and the only operation allowed on them is equality testing. For example, the golfers in the social golfer problem are indistinguishable. If we do label the golfers, then any relabelling of the golfers in one solution gives another valid solution. Therefore, we can regard the symmetric group of size $n$ as acting on a set of $n$ indistinguishable objects. In this paper, we show how we can break the symmetries resulting from indistinguishable objects. We show how symmetries on indistinguishable objects can be defined properly in complex types, for example in a matrix indexed by indistinguishable objects. We then show how the resulting symmetries can be broken correctly. In Essence, a high-level modelling language, indistinguishable objects are encapsulated in "unnamed types". We provide an implementation of complete symmetry breaking for unnamed types in Essence.

Behaviour Planning: A Toolkit for Diverse Planning

Diverse planning is the problem of generating plans with distinct characteristics. This is valuable for many real-world scenarios, including applications related to plan recognition and business process automation. In this work, we introduce \emph{Behaviour Planning}, a diverse planning toolkit that can characterise and generate diverse plans based on modular diversity models. We present a qualitative framework for describing diversity models, a planning approach for generating plans aligned with any given diversity model, and provide a practical implementation of an SMT-based behaviour planner. We showcase how the qualitative approach offered by Behaviour Planning allows it to overcome various challenges faced by previous approaches. Finally, the experimental evaluation shows the effectiveness of Behaviour Planning in generating diverse plans compared to state-of-the-art approaches.

Bridging the Gap between Structural and Semantic Similarity in Diverse Planning

Diverse planning is the problem of finding multiple plans for a given problem specification, which is at the core of many real-world applications. For example, diverse planning is a critical piece for the efficiency of plan recognition systems when dealing with noisy and missing observations. Providing diverse solutions can also benefit situations where constraints are too expensive or impossible to model. Current diverse planners operate by generating multiple plans and then applying a selection procedure to extract diverse solutions using a similarity metric. Generally, current similarity metrics only consider the structural properties of the given plans. We argue that this approach is a limitation that sometimes prevents such metrics from capturing why two plans differ. In this work, we propose two new domain-independent metrics which are able to capture relevant information on the difference between two given plans from a domain-dependent viewpoint. We showcase their utility in various situations where the currently used metrics fail to capture the similarity between plans, failing to capture some structural symmetries.

Towards a Model of Puzznic

We report on progress in modelling and solving Puzznic, a video game requiring the player to plan sequences of moves to clear a grid by matching blocks. We focus here on levels with no moving blocks. We compare a planning approach and three constraint programming approaches on a small set of benchmark instances. The planning approach is at present superior to the constraint programming approaches, but we outline proposals for improving the constraint models.

Automatic Tabulation in Constraint Models

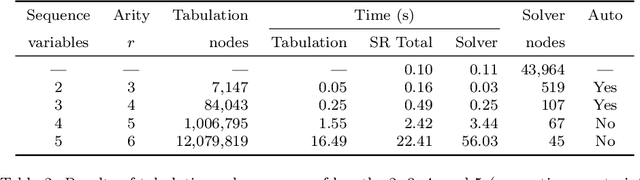
The performance of a constraint model can often be improved by converting a subproblem into a single table constraint. In this paper we study heuristics for identifying promising candidate subproblems, where converting the candidate into a table constraint is likely to improve solver performance. We propose a small set of heuristics to identify common cases, such as expressions that will propagate weakly. The process of discovering promising subproblems and tabulating them is entirely automated in the constraint modelling tool Savile Row. Caches are implemented to avoid tabulating equivalent subproblems many times. We give a simple algorithm to generate table constraints directly from a constraint expression in \savilerow. We demonstrate good performance on the benchmark problems used in earlier work on tabulation, and also for several new problem classes. In some cases, the entirely automated process leads to orders of magnitude improvements in solver performance.

Towards Reformulating Essence Specifications for Robustness

The Essence language allows a user to specify a constraint problem at a level of abstraction above that at which constraint modelling decisions are made. Essence specifications are refined into constraint models using the Conjure automated modelling tool, which employs a suite of refinement rules. However, Essence is a rich language in which there are many equivalent ways to specify a given problem. A user may therefore omit the use of domain attributes or abstract types, resulting in fewer refinement rules being applicable and therefore a reduced set of output models from which to select. This paper addresses the problem of recovering this information automatically to increase the robustness of the quality of the output constraint models in the face of variation in the input Essence specification. We present reformulation rules that can change the type of a decision variable or add attributes that shrink its domain. We demonstrate the efficacy of this approach in terms of the quantity and quality of models Conjure can produce from the transformed specification compared with the original.

Using Small MUSes to Explain How to Solve Pen and Paper Puzzles

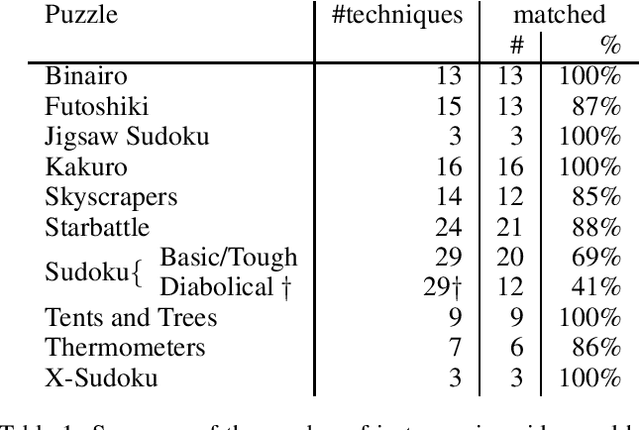
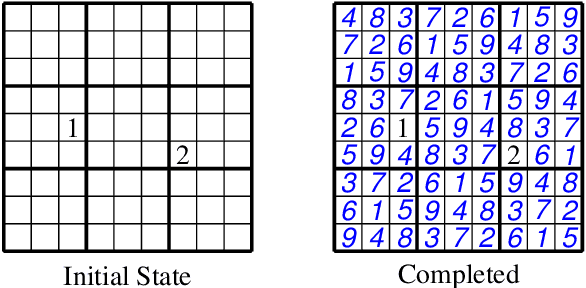
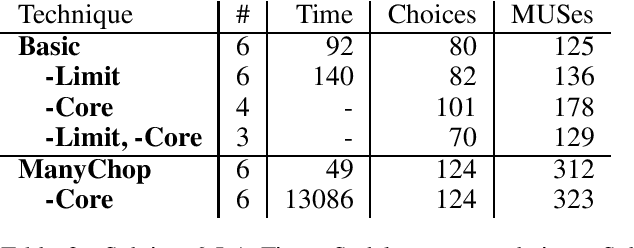
Pen and paper puzzles like Sudoku, Futoshiki and Skyscrapers are hugely popular. Solving such puzzles can be a trivial task for modern AI systems. However, most AI systems solve problems using a form of backtracking, while people try to avoid backtracking as much as possible. This means that existing AI systems do not output explanations about their reasoning that are meaningful to people. We present Demystify, a tool which allows puzzles to be expressed in a high-level constraint programming language and uses MUSes to allow us to produce descriptions of steps in the puzzle solving. We give several improvements to the existing techniques for solving puzzles with MUSes, which allow us to solve a range of significantly more complex puzzles and give higher quality explanations. We demonstrate the effectiveness and generality of Demystify by comparing its results to documented strategies for solving a range of pen and paper puzzles by hand, showing that our technique can find many of the same explanations.

The Winnability of Klondike and Many Other Single-Player Card Games

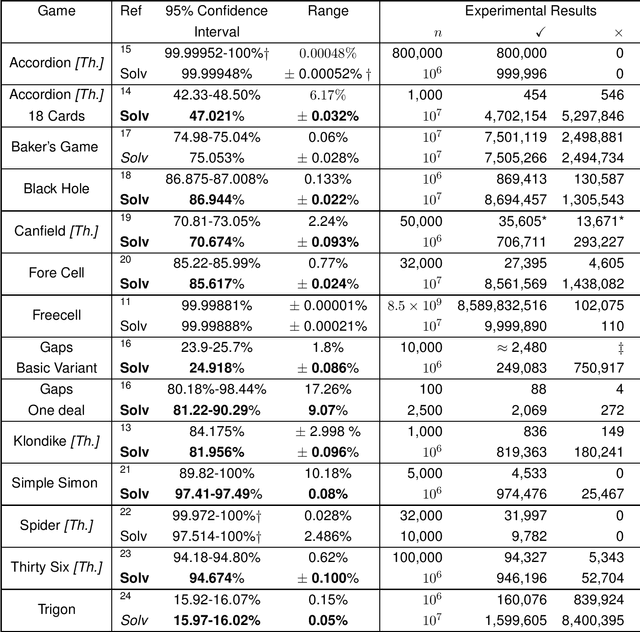
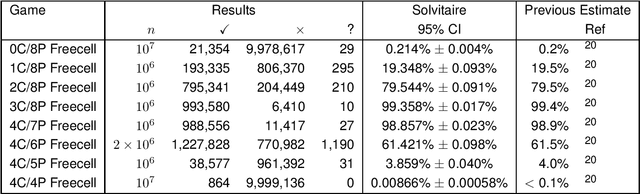
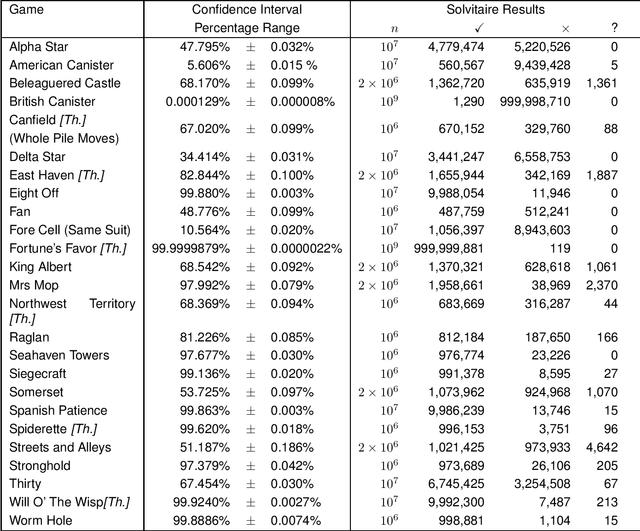
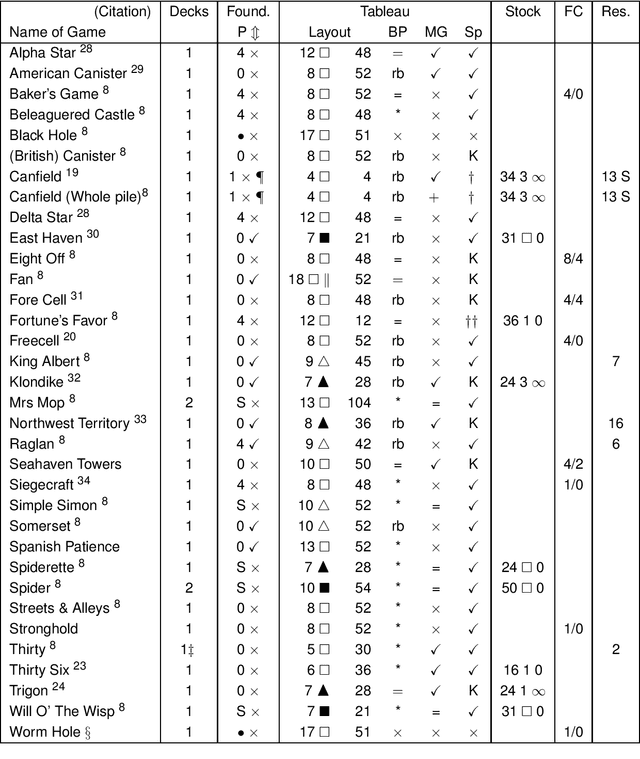
The most famous single-player card game is 'Klondike', but our ignorance of its winnability percentage has been called "one of the embarrassments of applied mathematics". Klondike is just one of many single-player card games, generically called 'patience' or 'solitaire' games, for which players have long wanted to know how likely a particular game is to be winnable for a random deal. A number of different games have been studied empirically in the academic literature and by non-academic enthusiasts. Here we show that a single general purpose Artificial Intelligence program, called "Solvitaire", can be used to determine the winnability percentage of approximately 30 different single-player card games with a 95\% confidence interval of +/- 0.1\% or better. For example, we report the winnability of Klondike as 81.956% +/- 0.096% (in the 'thoughtful' variant where the player knows the location of all cards), a 30-fold reduction in confidence interval over the best previous result. Almost all our results are either entirely new or represent significant improvements on previous knowledge.