Towards Reformulating Essence Specifications for Robustness

The Essence language allows a user to specify a constraint problem at a level of abstraction above that at which constraint modelling decisions are made. Essence specifications are refined into constraint models using the Conjure automated modelling tool, which employs a suite of refinement rules. However, Essence is a rich language in which there are many equivalent ways to specify a given problem. A user may therefore omit the use of domain attributes or abstract types, resulting in fewer refinement rules being applicable and therefore a reduced set of output models from which to select. This paper addresses the problem of recovering this information automatically to increase the robustness of the quality of the output constraint models in the face of variation in the input Essence specification. We present reformulation rules that can change the type of a decision variable or add attributes that shrink its domain. We demonstrate the efficacy of this approach in terms of the quantity and quality of models Conjure can produce from the transformed specification compared with the original.

A Commentary on "Breaking Row and Column Symmetries in Matrix Models"

The CP 2002 paper entitled "Breaking Row and Column Symmetries in Matrix Models" by Flener et al. (https://link.springer.com/chapter/10.1007%2F3-540-46135-3_31) describes some of the first work for identifying and analyzing row and column symmetry in matrix models and for efficiently and effectively dealing with such symmetry using static symmetry-breaking ordering constraints. This commentary provides a retrospective on that work and highlights some of the subsequent work on the topic.

Convergent Deduction for Probabilistic Logic

This paper discusses the semantics and proof theory of Nilsson's probabilistic logic, outlining both the benefits of its well-defined model theory and the drawbacks of its proof theory. Within Nilsson's semantic framework, we derive a set of inference rules which are provably sound. The resulting proof system, in contrast to Nilsson's approach, has the important feature of convergence - that is, the inference process proceeds by computing increasingly narrow probability intervals which converge from above and below on the smallest entailed probability interval. Thus the procedure can be stopped at any time to yield partial information concerning the smallest entailed interval.

Probability as a Modal Operator

This paper argues for a modal view of probability. The syntax and semantics of one particularly strong probability logic are discussed and some examples of the use of the logic are provided. We show that it is both natural and useful to think of probability as a modal operator. Contrary to popular belief in AI, a probability ranging between 0 and 1 represents a continuum between impossibility and necessity, not between simple falsity and truth. The present work provides a clear semantics for quantification into the scope of the probability operator and for higher-order probabilities. Probability logic is a language for expressing both probabilistic and logical concepts.

Conjure Revisited: Towards Automated Constraint Modelling

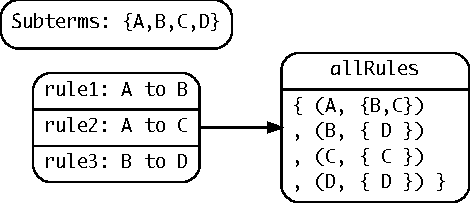
Automating the constraint modelling process is one of the key challenges facing the constraints field, and one of the principal obstacles preventing widespread adoption of constraint solving. This paper focuses on the refinement-based approach to automated modelling, where a user specifies a problem in an abstract constraint specification language and it is then automatically refined into a constraint model. In particular, we revisit the Conjure system that first appeared in prototype form in 2005 and present a new implementation with a much greater coverage of the specification language Essence.

Multiset Ordering Constraints

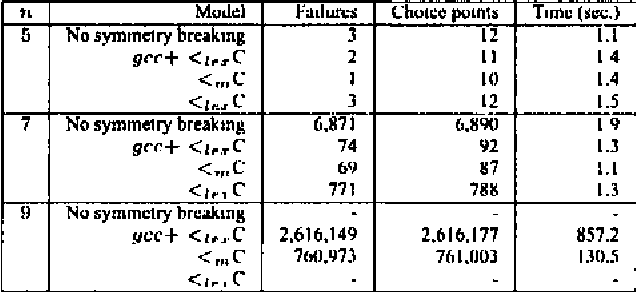
We identify a new and important global (or non-binary) constraint. This constraint ensures that the values taken by two vectors of variables, when viewed as multisets, are ordered. This constraint is useful for a number of different applications including breaking symmetry and fuzzy constraint satisfaction. We propose and implement an efficient linear time algorithm for enforcing generalised arc consistency on such a multiset ordering constraint. Experimental results on several problem domains show considerable promise.