Zeynep Kiziltan
Determining Energy Efficiency Sweet Spots in Production LLM Inference
Feb 05, 2026Abstract:Large Language Models (LLMs) inference is central in modern AI applications, making it critical to understand their energy footprint. Existing approaches typically estimate energy consumption through simple linear functions of input and output sequence lengths, yet our observations reveal clear Energy Efficiency regimes: peak efficiency occurs with short-to-moderate inputs and medium-length outputs, while efficiency drops sharply for long inputs or very short outputs, indicating a non-linear dependency. In this work, we propose an analytical model derived from the computational and memory-access complexity of the Transformer architecture, capable of accurately characterizing the efficiency curve as a function of input and output lengths. To assess its accuracy, we evaluate energy consumption using TensorRT-LLM on NVIDIA H100 GPUs across a diverse set of LLMs ranging from 1B to 9B parameters, including OPT, LLaMA, Gemma, Falcon, Qwen2, and Granite, tested over input and output lengths from 64 to 4096 tokens, achieving a mean MAPE of 1.79%. Our results show that aligning sequence lengths with these efficiency "Sweet Spots" can substantially reduce energy usage, supporting informed truncation, summarization, and adaptive generation strategies in production systems.
Automatic Tabulation in Constraint Models
Feb 26, 2022


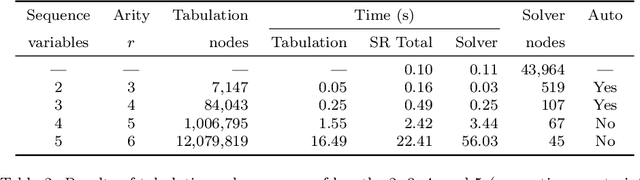
Abstract:The performance of a constraint model can often be improved by converting a subproblem into a single table constraint. In this paper we study heuristics for identifying promising candidate subproblems, where converting the candidate into a table constraint is likely to improve solver performance. We propose a small set of heuristics to identify common cases, such as expressions that will propagate weakly. The process of discovering promising subproblems and tabulating them is entirely automated in the constraint modelling tool Savile Row. Caches are implemented to avoid tabulating equivalent subproblems many times. We give a simple algorithm to generate table constraints directly from a constraint expression in \savilerow. We demonstrate good performance on the benchmark problems used in earlier work on tabulation, and also for several new problem classes. In some cases, the entirely automated process leads to orders of magnitude improvements in solver performance.
A Constraint Programming-based Job Dispatcher for Modern HPC Systems and Applications
Sep 28, 2020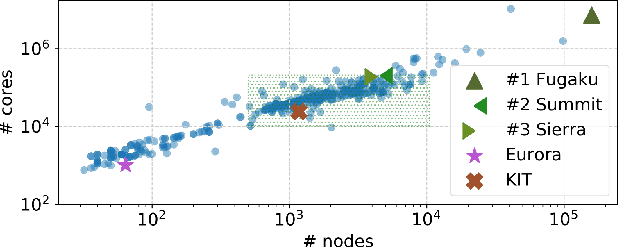

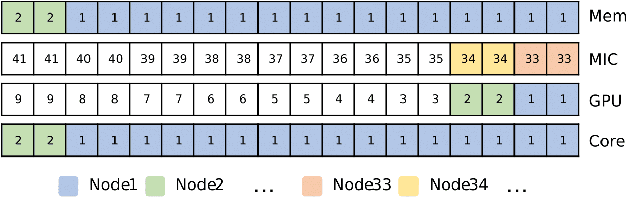

Abstract:Constraint Programming (CP) is a well-established area in AI as a programming paradigm for modelling and solving discrete optimization problems, and it has been been successfully applied to tackle the on-line job dispatching problem in HPC systems including those running modern applications. The limitations of the available CP-based job dispatchers may hinder their practical use in today's systems that are becoming larger in size and more demanding in resource allocation. In an attempt to bring basic AI research closer to a deployed application, we present a new CP-based on-line job dispatcher for modern HPC systems and applications. Unlike its predecessors, our new dispatcher tackles the entire problem in CP and its model size is independent of the system size. Experimental results based on a simulation study show that with our approach dispatching performance increases significantly in a large system and in a system where allocation is nontrivial.
A Machine Learning Approach to Online Fault Classification in HPC Systems
Jul 27, 2020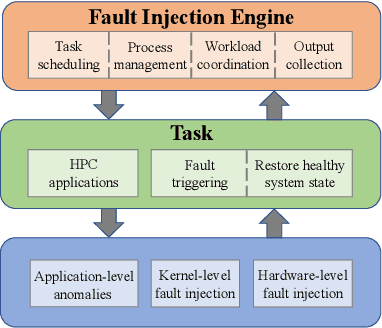
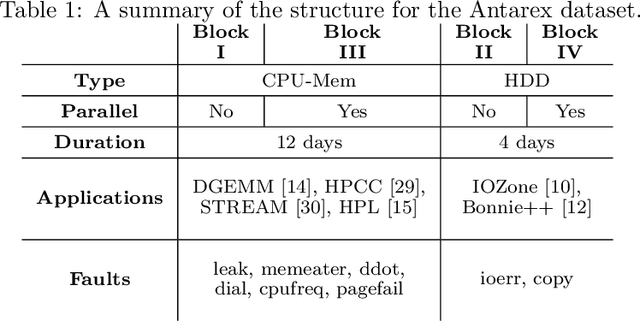
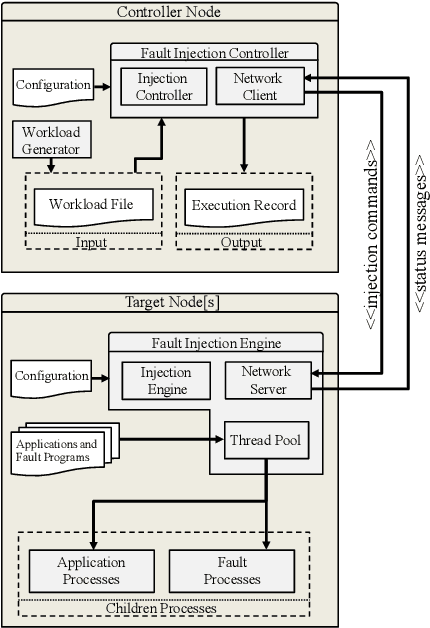

Abstract:As High-Performance Computing (HPC) systems strive towards the exascale goal, failure rates both at the hardware and software levels will increase significantly. Thus, detecting and classifying faults in HPC systems as they occur and initiating corrective actions before they can transform into failures becomes essential for continued operation. Central to this objective is fault injection, which is the deliberate triggering of faults in a system so as to observe their behavior in a controlled environment. In this paper, we propose a fault classification method for HPC systems based on machine learning. The novelty of our approach rests with the fact that it can be operated on streamed data in an online manner, thus opening the possibility to devise and enact control actions on the target system in real-time. We introduce a high-level, easy-to-use fault injection tool called FINJ, with a focus on the management of complex experiments. In order to train and evaluate our machine learning classifiers, we inject faults to an in-house experimental HPC system using FINJ, and generate a fault dataset which we describe extensively. Both FINJ and the dataset are publicly available to facilitate resiliency research in the HPC systems field. Experimental results demonstrate that our approach allows almost perfect classification accuracy to be reached for different fault types with low computational overhead and minimal delay.
* arXiv admin note: text overlap with arXiv:1807.10056, arXiv:1810.11208
A Commentary on "Breaking Row and Column Symmetries in Matrix Models"
Oct 03, 2019
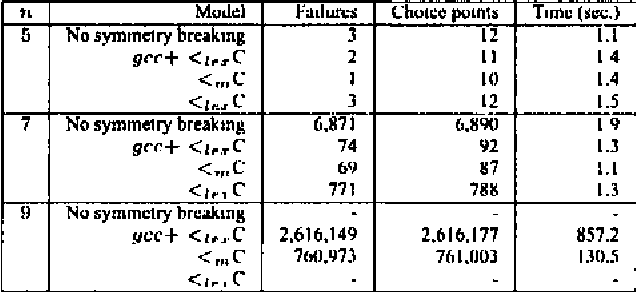
Abstract:The CP 2002 paper entitled "Breaking Row and Column Symmetries in Matrix Models" by Flener et al. (https://link.springer.com/chapter/10.1007%2F3-540-46135-3_31) describes some of the first work for identifying and analyzing row and column symmetry in matrix models and for efficiently and effectively dealing with such symmetry using static symmetry-breaking ordering constraints. This commentary provides a retrospective on that work and highlights some of the subsequent work on the topic.
Multiset Ordering Constraints
May 22, 2009

Abstract:We identify a new and important global (or non-binary) constraint. This constraint ensures that the values taken by two vectors of variables, when viewed as multisets, are ordered. This constraint is useful for a number of different applications including breaking symmetry and fuzzy constraint satisfaction. We propose and implement an efficient linear time algorithm for enforcing generalised arc consistency on such a multiset ordering constraint. Experimental results on several problem domains show considerable promise.
* Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence (IJCAI-03)
SLIDE: A Useful Special Case of the CARDPATH Constraint
Mar 03, 2009
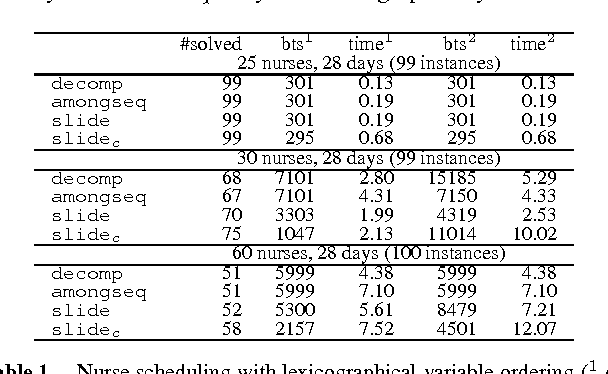
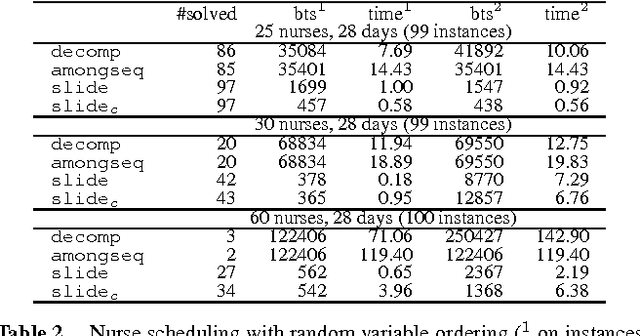
Abstract:We study the CardPath constraint. This ensures a given constraint holds a number of times down a sequence of variables. We show that SLIDE, a special case of CardPath where the slid constraint must hold always, can be used to encode a wide range of sliding sequence constraints including CardPath itself. We consider how to propagate SLIDE and provide a complete propagator for CardPath. Since propagation is NP-hard in general, we identify special cases where propagation takes polynomial time. Our experiments demonstrate that using SLIDE to encode global constraints can be as efficient and effective as specialised propagators.
* 18th European Conference on Artificial Intelligence
The Parameterized Complexity of Global Constraints
Mar 03, 2009Abstract:We argue that parameterized complexity is a useful tool with which to study global constraints. In particular, we show that many global constraints which are intractable to propagate completely have natural parameters which make them fixed-parameter tractable and which are easy to compute. This tractability tends either to be the result of a simple dynamic program or of a decomposition which has a strong backdoor of bounded size. This strong backdoor is often a cycle cutset. We also show that parameterized complexity can be used to study other aspects of constraint programming like symmetry breaking. For instance, we prove that value symmetry is fixed-parameter tractable to break in the number of symmetries. Finally, we argue that parameterized complexity can be used to derive results about the approximability of constraint propagation.
* Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence
Filtering Algorithms for the Multiset Ordering Constraint
Mar 03, 2009



Abstract:Constraint programming (CP) has been used with great success to tackle a wide variety of constraint satisfaction problems which are computationally intractable in general. Global constraints are one of the important factors behind the success of CP. In this paper, we study a new global constraint, the multiset ordering constraint, which is shown to be useful in symmetry breaking and searching for leximin optimal solutions in CP. We propose efficient and effective filtering algorithms for propagating this global constraint. We show that the algorithms are sound and complete and we discuss possible extensions. We also consider alternative propagation methods based on existing constraints in CP toolkits. Our experimental results on a number of benchmark problems demonstrate that propagating the multiset ordering constraint via a dedicated algorithm can be very beneficial.
Range and Roots: Two Common Patterns for Specifying and Propagating Counting and Occurrence Constraints
Mar 02, 2009



Abstract:We propose Range and Roots which are two common patterns useful for specifying a wide range of counting and occurrence constraints. We design specialised propagation algorithms for these two patterns. Counting and occurrence constraints specified using these patterns thus directly inherit a propagation algorithm. To illustrate the capabilities of the Range and Roots constraints, we specify a number of global constraints taken from the literature. Preliminary experiments demonstrate that propagating counting and occurrence constraints using these two patterns leads to a small loss in performance when compared to specialised global constraints and is competitive with alternative decompositions using elementary constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge