Learning to Select SAT Encodings for Pseudo-Boolean and Linear Integer Constraints

Many constraint satisfaction and optimisation problems can be solved effectively by encoding them as instances of the Boolean Satisfiability problem (SAT). However, even the simplest types of constraints have many encodings in the literature with widely varying performance, and the problem of selecting suitable encodings for a given problem instance is not trivial. We explore the problem of selecting encodings for pseudo-Boolean and linear constraints using a supervised machine learning approach. We show that it is possible to select encodings effectively using a standard set of features for constraint problems; however we obtain better performance with a new set of features specifically designed for the pseudo-Boolean and linear constraints. In fact, we achieve good results when selecting encodings for unseen problem classes. Our results compare favourably to AutoFolio when using the same feature set. We discuss the relative importance of instance features to the task of selecting the best encodings, and compare several variations of the machine learning method.

Automatic Tabulation in Constraint Models

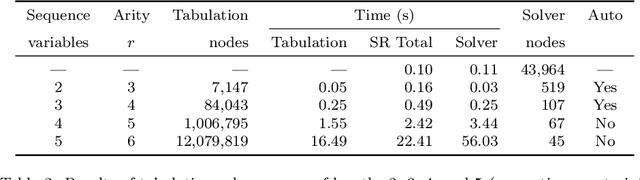
The performance of a constraint model can often be improved by converting a subproblem into a single table constraint. In this paper we study heuristics for identifying promising candidate subproblems, where converting the candidate into a table constraint is likely to improve solver performance. We propose a small set of heuristics to identify common cases, such as expressions that will propagate weakly. The process of discovering promising subproblems and tabulating them is entirely automated in the constraint modelling tool Savile Row. Caches are implemented to avoid tabulating equivalent subproblems many times. We give a simple algorithm to generate table constraints directly from a constraint expression in \savilerow. We demonstrate good performance on the benchmark problems used in earlier work on tabulation, and also for several new problem classes. In some cases, the entirely automated process leads to orders of magnitude improvements in solver performance.

SAT Encodings for Pseudo-Boolean Constraints Together With At-Most-One Constraints

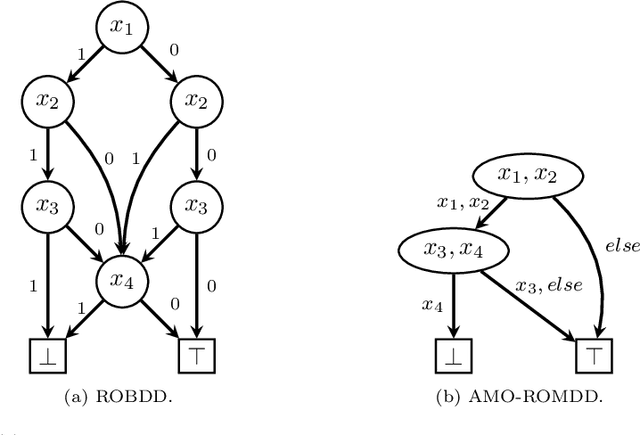
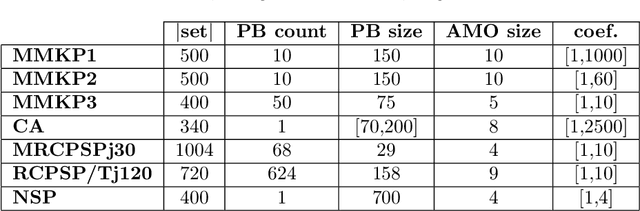
When solving a combinatorial problem using propositional satisfiability (SAT), the encoding of the problem is of vital importance. We study encodings of Pseudo-Boolean (PB) constraints, a common type of arithmetic constraint that appears in a wide variety of combinatorial problems such as timetabling, scheduling, and resource allocation. In some cases PB constraints occur together with at-most-one (AMO) constraints over subsets of their variables (forming PB(AMO) constraints). Recent work has shown that taking account of AMOs when encoding PB constraints using decision diagrams can produce a dramatic improvement in solver efficiency. In this paper we extend the approach to other state-of-the-art encodings of PB constraints, developing several new encodings for PB(AMO) constraints. Also, we present a more compact and efficient version of the popular Generalized Totalizer encoding, named Reduced Generalized Totalizer. This new encoding is also adapted for PB(AMO) constraints for a further gain. Our experiments show that the encodings of PB(AMO) constraints can be substantially smaller than those of PB constraints. PB(AMO) encodings allow many more instances to be solved within a time limit, and solving time is improved by more than one order of magnitude in some cases. We also observed that there is no single overall winner among the considered encodings, but efficiency of each encoding may depend on PB(AMO) characteristics such as the magnitude of coefficient values.