A Metric Hybrid Planning Approach to Solving Pandemic Planning Problems with Simple SIR Models

A pandemic is the spread of a disease across large regions, and can have devastating costs to the society in terms of health, economic and social. As such, the study of effective pandemic mitigation strategies can yield significant positive impact on the society. A pandemic can be mathematically described using a compartmental model, such as the Susceptible Infected Removed (SIR) model. In this paper, we extend the solution equations of the SIR model to a state transition model with lockdowns. We formalize a metric hybrid planning problem based on this state transition model, and solve it using a metric hybrid planner. We improve the runtime effectiveness of the metric hybrid planner with the addition of valid inequalities, and demonstrate the success of our approach both theoretically and experimentally under various challenging settings.

Training Experimentally Robust and Interpretable Binarized Regression Models Using Mixed-Integer Programming

In this paper, we explore model-based approach to training robust and interpretable binarized regression models for multiclass classification tasks using Mixed-Integer Programming (MIP). Our MIP model balances the optimization of prediction margin and model size by using a weighted objective that: minimizes the total margin of incorrectly classified training instances, maximizes the total margin of correctly classified training instances, and maximizes the overall model regularization. We conduct two sets of experiments to test the classification accuracy of our MIP model over standard and corrupted versions of multiple classification datasets, respectively. In the first set of experiments, we show that our MIP model outperforms an equivalent Pseudo-Boolean Optimization (PBO) model and achieves competitive results to Logistic Regression (LR) and Gradient Descent (GD) in terms of classification accuracy over the standard datasets. In the second set of experiments, we show that our MIP model outperforms the other models (i.e., GD and LR) in terms of classification accuracy over majority of the corrupted datasets. Finally, we visually demonstrate the interpretability of our MIP model in terms of its learned parameters over the MNIST dataset. Overall, we show the effectiveness of training robust and interpretable binarized regression models using MIP.

Planning with Learned Binarized Neural Networks Benchmarks for MaxSAT Evaluation 2021

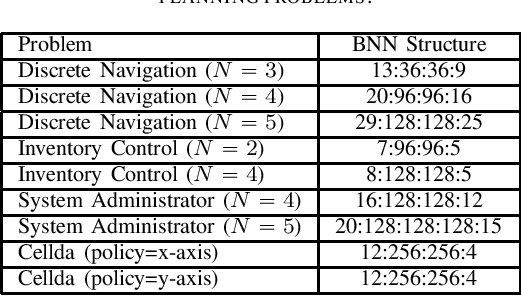
This document provides a brief introduction to learned automated planning problem where the state transition function is in the form of a binarized neural network (BNN), presents a general MaxSAT encoding for this problem, and describes the four domains, namely: Navigation, Inventory Control, System Administrator and Cellda, that are submitted as benchmarks for MaxSAT Evaluation 2021.

Reward Potentials for Planning with Learned Neural Network Transition Models

Optimal planning with respect to learned neural network (NN) models in continuous action and state spaces using mixed-integer linear programming (MILP) is a challenging task for branch-and-bound solvers due to the poor linear relaxation of the underlying MILP model. For a given set of features, potential heuristics provide an efficient framework for computing bounds on cost (reward) functions. In this paper, we model the problem of finding an optimal potential bounds for learned NN models as a bilevel program, and solve it using a novel finite-time constraint generation algorithm. We then strengthen the linear relaxation of the underlying MILP model by introducing constraints to bound the reward function based on the precomputed reward potentials. Experimentally, we show that our algorithm efficiently computes reward potentials for learned NN models, and the overhead of computing reward potentials is justified by the overall strengthening of the underlying MILP model for the task of planning over long horizons.

Scalable Nonlinear Planning with Deep Neural Network Learned Transition Models

In many real-world planning problems with factored, mixed discrete and continuous state and action spaces such as Reservoir Control, Heating Ventilation, and Air Conditioning, and Navigation domains, it is difficult to obtain a model of the complex nonlinear dynamics that govern state evolution. However, the ubiquity of modern sensors allows us to collect large quantities of data from each of these complex systems and build accurate, nonlinear deep neural network models of their state transitions. But there remains one major problem for the task of control -- how can we plan with deep network learned transition models without resorting to Monte Carlo Tree Search and other black-box transition model techniques that ignore model structure and do not easily extend to mixed discrete and continuous domains? In this paper, we introduce two types of nonlinear planning methods that can leverage deep neural network learned transition models: Hybrid Deep MILP Planner (HD-MILP-Plan) and Tensorflow Planner (TF-Plan). In HD-MILP-Plan, we make the critical observation that the Rectified Linear Unit transfer function for deep networks not only allows faster convergence of model learning, but also permits a direct compilation of the deep network transition model to a Mixed-Integer Linear Program encoding. Further, we identify deep network specific optimizations for HD-MILP-Plan that improve performance over a base encoding and show that we can plan optimally with respect to the learned deep networks. In TF-Plan, we take advantage of the efficiency of auto-differentiation tools and GPU-based computation where we encode a subclass of purely continuous planning problems as Recurrent Neural Networks and directly optimize the actions through backpropagation. We compare both planners and show that TF-Plan is able to approximate the optimal plans found by HD-MILP-Plan in less computation time...

Compact and Efficient Encodings for Planning in Factored State and Action Spaces with Learned Binarized Neural Network Transition Models

In this paper, we leverage the efficiency of Binarized Neural Networks (BNNs) to learn complex state transition models of planning domains with discretized factored state and action spaces. In order to directly exploit this transition structure for planning, we present two novel compilations of the learned factored planning problem with BNNs based on reductions to Weighted Partial Maximum Boolean Satisfiability (FD-SAT-Plan+) as well as Binary Linear Programming (FD-BLP-Plan+). Theoretically, we show that our SAT-based Bi-Directional Neuron Activation Encoding is asymptotically the most compact encoding in the literature and maintains the generalized arc-consistency property through unit propagation -- an important property that facilitates efficiency in SAT solvers. Experimentally, we validate the computational efficiency of our Bi-Directional Neuron Activation Encoding in comparison to an existing neuron activation encoding and demonstrate the effectiveness of learning complex transition models with BNNs. We test the runtime efficiency of both FD-SAT-Plan+ and FD-BLP-Plan+ on the learned factored planning problem showing that FD-SAT-Plan+ scales better with increasing BNN size and complexity. Finally, we present a finite-time incremental constraint generation algorithm based on generalized landmark constraints to improve the planning accuracy of our encodings through simulated or real-world interaction.

Scalable Planning with Tensorflow for Hybrid Nonlinear Domains

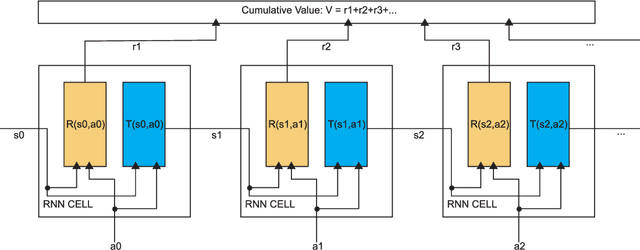
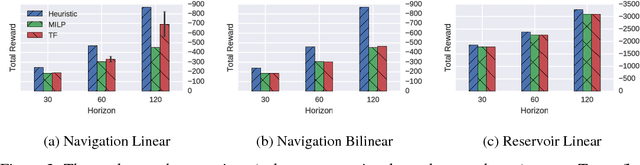
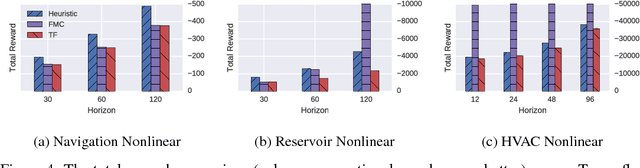
Given recent deep learning results that demonstrate the ability to effectively optimize high-dimensional non-convex functions with gradient descent optimization on GPUs, we ask in this paper whether symbolic gradient optimization tools such as Tensorflow can be effective for planning in hybrid (mixed discrete and continuous) nonlinear domains with high dimensional state and action spaces? To this end, we demonstrate that hybrid planning with Tensorflow and RMSProp gradient descent is competitive with mixed integer linear program (MILP) based optimization on piecewise linear planning domains (where we can compute optimal solutions) and substantially outperforms state-of-the-art interior point methods for nonlinear planning domains. Furthermore, we remark that Tensorflow is highly scalable, converging to a strong plan on a large-scale concurrent domain with a total of 576,000 continuous action parameters distributed over a horizon of 96 time steps and 100 parallel instances in only 4 minutes. We provide a number of insights that clarify such strong performance including observations that despite long horizons, RMSProp avoids both the vanishing and exploding gradient problems. Together these results suggest a new frontier for highly scalable planning in nonlinear hybrid domains by leveraging GPUs and the power of recent advances in gradient descent with highly optimized toolkits like Tensorflow.