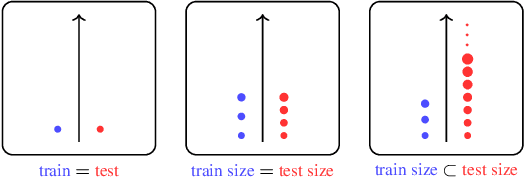
AI Planning: A Primer and Survey (Preliminary Report)

Automated decision-making is a fundamental topic that spans multiple sub-disciplines in AI: reinforcement learning (RL), AI planning (AP), foundation models, and operations research, among others. Despite recent efforts to ``bridge the gaps'' between these communities, there remain many insights that have not yet transcended the boundaries. Our goal in this paper is to provide a brief and non-exhaustive primer on ideas well-known in AP, but less so in other sub-disciplines. We do so by introducing the classical AP problem and representation, and extensions that handle uncertainty and time through the Markov Decision Process formalism. Next, we survey state-of-the-art techniques and ideas for solving AP problems, focusing on their ability to exploit problem structure. Lastly, we cover subfields within AP for learning structure from unstructured inputs and learning to generalise to unseen scenarios and situations.

Graph Learning for Planning: The Story Thus Far and Open Challenges

Graph learning is naturally well suited for use in planning due to its ability to exploit relational structures exhibited in planning domains and to take as input planning instances with arbitrary number of objects. In this paper, we study the usage of graph learning for planning thus far by studying the theoretical and empirical effects on learning and planning performance of (1) graph representations of planning tasks, (2) graph learning architectures, and (3) optimisation formulations for learning. Our studies accumulate in the GOOSE framework which learns domain knowledge from small planning tasks in order to scale up to much larger planning tasks. In this paper, we also highlight and propose the 5 open challenges in the general Learning for Planning field that we believe need to be addressed for advancing the state-of-the-art.

Graph Learning for Numeric Planning

Graph learning is naturally well suited for use in symbolic, object-centric planning due to its ability to exploit relational structures exhibited in planning domains and to take as input planning instances with arbitrary numbers of objects. Numeric planning is an extension of symbolic planning in which states may now also exhibit numeric variables. In this work, we propose data-efficient and interpretable machine learning models for learning to solve numeric planning tasks. This involves constructing a new graph kernel for graphs with both continuous and categorical attributes, as well as new optimisation methods for learning heuristic functions for numeric planning. Experiments show that our graph kernels are vastly more efficient and generalise better than graph neural networks for numeric planning, and also yield competitive coverage performance compared to domain-independent numeric planners. Code is available at https://github.com/DillonZChen/goose

Novelty Heuristics, Multi-Queue Search, and Portfolios for Numeric Planning

Heuristic search is a powerful approach for solving planning problems and numeric planning is no exception. In this paper, we boost the performance of heuristic search for numeric planning with various powerful techniques orthogonal to improving heuristic informedness: numeric novelty heuristics, the Manhattan distance heuristic, and exploring the use of multi-queue search and portfolios for combining heuristics.

Return to Tradition: Learning Reliable Heuristics with Classical Machine Learning

Current approaches for learning for planning have yet to achieve competitive performance against classical planners in several domains, and have poor overall performance. In this work, we construct novel graph representations of lifted planning tasks and use the WL algorithm to generate features from them. These features are used with classical machine learning methods which have up to 2 orders of magnitude fewer parameters and train up to 3 orders of magnitude faster than the state-of-the-art deep learning for planning models. Our novel approach, WL-GOOSE, reliably learns heuristics from scratch and outperforms the $h^{\text{FF}}$ heuristic in a fair competition setting. It also outperforms or ties with LAMA on 4 out of 10 domains on coverage and 7 out of 10 domains on plan quality. WL-GOOSE is the first learning for planning model which achieves these feats. Furthermore, we study the connections between our novel WL feature generation method, previous theoretically flavoured learning architectures, and Description Logic Features for planning.

Learning Domain-Independent Heuristics for Grounded and Lifted Planning

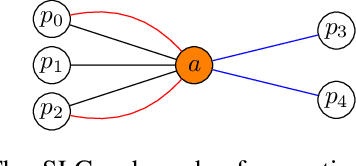
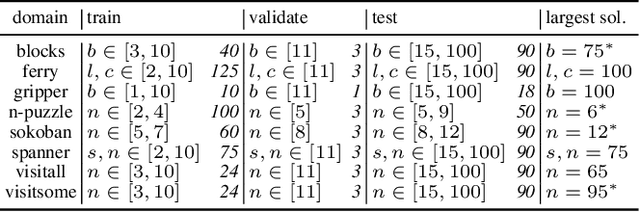
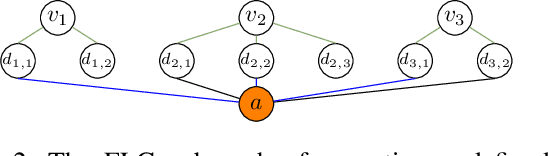
We present three novel graph representations of planning tasks suitable for learning domain-independent heuristics using Graph Neural Networks (GNNs) to guide search. In particular, to mitigate the issues caused by large grounded GNNs we present the first method for learning domain-independent heuristics with only the lifted representation of a planning task. We also provide a theoretical analysis of the expressiveness of our models, showing that some are more powerful than STRIPS-HGN, the only other existing model for learning domain-independent heuristics. Our experiments show that our heuristics generalise to much larger problems than those in the training set, vastly surpassing STRIPS-HGN heuristics.

A More General Theory of Diagnosis from First Principles

Model-based diagnosis has been an active research topic in different communities including artificial intelligence, formal methods, and control. This has led to a set of disparate approaches addressing different classes of systems and seeking different forms of diagnoses. In this paper, we resolve such disparities by generalising Reiter's theory to be agnostic to the types of systems and diagnoses considered. This more general theory of diagnosis from first principles defines the minimal diagnosis as the set of preferred diagnosis candidates in a search space of hypotheses. Computing the minimal diagnosis is achieved by exploring the space of diagnosis hypotheses, testing sets of hypotheses for consistency with the system's model and the observation, and generating conflicts that rule out successors and other portions of the search space. Under relatively mild assumptions, our algorithms correctly compute the set of preferred diagnosis candidates. The main difficulty here is that the search space is no longer a powerset as in Reiter's theory, and that, as consequence, many of the implicit properties (such as finiteness of the search space) no longer hold. The notion of conflict also needs to be generalised and we present such a more general notion. We present two implementations of these algorithms, using test solvers based on satisfiability and heuristic search, respectively, which we evaluate on instances from two real world discrete event problems. Despite the greater generality of our theory, these implementations surpass the special purpose algorithms designed for discrete event systems, and enable solving instances that were out of reach of existing diagnosis approaches.

Heuristic Search for Multi-Objective Probabilistic Planning

Heuristic search is a powerful approach that has successfully been applied to a broad class of planning problems, including classical planning, multi-objective planning, and probabilistic planning modelled as a stochastic shortest path (SSP) problem. Here, we extend the reach of heuristic search to a more expressive class of problems, namely multi-objective stochastic shortest paths (MOSSPs), which require computing a coverage set of non-dominated policies. We design new heuristic search algorithms MOLAO* and MOLRTDP, which extend well-known SSP algorithms to the multi-objective case. We further construct a spectrum of domain-independent heuristic functions differing in their ability to take into account the stochastic and multi-objective features of the problem to guide the search. Our experiments demonstrate the benefits of these algorithms and the relative merits of the heuristics.

Learning Domain-Independent Planning Heuristics with Hypergraph Networks

We present the first approach capable of learning domain-independent planning heuristics entirely from scratch. The heuristics we learn map the hypergraph representation of the delete-relaxation of the planning problem at hand, to a cost estimate that approximates that of the least-cost path from the current state to the goal through the hypergraph. We generalise Graph Networks to obtain a new framework for learning over hypergraphs, which we specialise to learn planning heuristics by training over state/value pairs obtained from optimal cost plans. Our experiments show that the resulting architecture, STRIPS-HGNs, is capable of learning heuristics that are competitive with existing delete-relaxation heuristics including LM-cut. We show that the heuristics we learn are able to generalise across different problems and domains, including to domains that were not seen during training.

ASNets: Deep Learning for Generalised Planning

In this paper, we discuss the learning of generalised policies for probabilistic and classical planning problems using Action Schema Networks (ASNets). The ASNet is a neural network architecture that exploits the relational structure of (P)PDDL planning problems to learn a common set of weights that can be applied to any problem in a domain. By mimicking the actions chosen by a traditional, non-learning planner on a handful of small problems in a domain, ASNets are able to learn a generalised reactive policy that can quickly solve much larger instances from the domain. This work extends the ASNet architecture to make it more expressive, while still remaining invariant to a range of symmetries that exist in PPDDL problems. We also present a thorough experimental evaluation of ASNets, including a comparison with heuristic search planners on seven probabilistic and deterministic domains, an extended evaluation on over 18,000 Blocksworld instances, and an ablation study. Finally, we show that sparsity-inducing regularisation can produce ASNets that are compact enough for humans to understand, yielding insights into how the structure of ASNets allows them to generalise across a domain.