A Universal Sets-level Optimization Framework for Next Set Recommendation

Next Set Recommendation (NSRec), encompassing related tasks such as next basket recommendation and temporal sets prediction, stands as a trending research topic. Although numerous attempts have been made on this topic, there are certain drawbacks: (i) Existing studies are still confined to utilizing objective functions commonly found in Next Item Recommendation (NIRec), such as binary cross entropy and BPR, which are calculated based on individual item comparisons; (ii) They place emphasis on building sophisticated learning models to capture intricate dependency relationships across sequential sets, but frequently overlook pivotal dependency in their objective functions; (iii) Diversity factor within sequential sets is frequently overlooked. In this research, we endeavor to unveil a universal and S ets-level optimization framework for N ext Set Recommendation (SNSRec), offering a holistic fusion of diversity distribution and intricate dependency relationships within temporal sets. To realize this, the following contributions are made: (i) We directly model the temporal set in a sequence as a cohesive entity, leveraging the Structured Determinantal Point Process (SDPP), wherein the probabilistic DPP distribution prioritizes collections of structures (sequential sets) instead of individual items; (ii) We introduce a co-occurrence representation to discern and acknowledge the importance of different sets; (iii) We propose a sets-level optimization criterion, which integrates the diversity distribution and dependency relations across the entire sequence of sets, guiding the model to recommend relevant and diversified set. Extensive experiments on real-world datasets show that our approach consistently outperforms previous methods on both relevance and diversity.

Learning k-Determinantal Point Processes for Personalized Ranking

The key to personalized recommendation is to predict a personalized ranking on a catalog of items by modeling the user's preferences. There are many personalized ranking approaches for item recommendation from implicit feedback like Bayesian Personalized Ranking (BPR) and listwise ranking. Despite these methods have shown performance benefits, there are still limitations affecting recommendation performance. First, none of them directly optimize ranking of sets, causing inadequate exploitation of correlations among multiple items. Second, the diversity aspect of recommendations is insufficiently addressed compared to relevance. In this work, we present a new optimization criterion LkP based on set probability comparison for personalized ranking that moves beyond traditional ranking-based methods. It formalizes set-level relevance and diversity ranking comparisons through a Determinantal Point Process (DPP) kernel decomposition. To confer ranking interpretability to the DPP set probabilities and prioritize the practicality of LkP, we condition the standard DPP on the cardinality k of the DPP-distributed set, known as k-DPP, a less-explored extension of DPP. The generic stochastic gradient descent based technique can be directly applied to optimizing models that employ LkP. We implement LkP in the context of both Matrix Factorization (MF) and neural networks approaches, on three real-world datasets, obtaining improved relevance and diversity performances. LkP is broadly applicable, and when applied to existing recommendation models it also yields strong performance improvements, suggesting that LkP holds significant value to the field of recommender systems.

Sampled Transformer for Point Sets

The sparse transformer can reduce the computational complexity of the self-attention layers to $O(n)$, whilst still being a universal approximator of continuous sequence-to-sequence functions. However, this permutation variant operation is not appropriate for direct application to sets. In this paper, we proposed an $O(n)$ complexity sampled transformer that can process point set elements directly without any additional inductive bias. Our sampled transformer introduces random element sampling, which randomly splits point sets into subsets, followed by applying a shared Hamiltonian self-attention mechanism to each subset. The overall attention mechanism can be viewed as a Hamiltonian cycle in the complete attention graph, and the permutation of point set elements is equivalent to randomly sampling Hamiltonian cycles. This mechanism implements a Monte Carlo simulation of the $O(n^2)$ dense attention connections. We show that it is a universal approximator for continuous set-to-set functions. Experimental results on point-clouds show comparable or better accuracy with significantly reduced computational complexity compared to the dense transformer or alternative sparse attention schemes.

Determinantal Point Process Likelihoods for Sequential Recommendation

Sequential recommendation is a popular task in academic research and close to real-world application scenarios, where the goal is to predict the next action(s) of the user based on his/her previous sequence of actions. In the training process of recommender systems, the loss function plays an essential role in guiding the optimization of recommendation models to generate accurate suggestions for users. However, most existing sequential recommendation techniques focus on designing algorithms or neural network architectures, and few efforts have been made to tailor loss functions that fit naturally into the practical application scenario of sequential recommender systems. Ranking-based losses, such as cross-entropy and Bayesian Personalized Ranking (BPR) are widely used in the sequential recommendation area. We argue that such objective functions suffer from two inherent drawbacks: i) the dependencies among elements of a sequence are overlooked in these loss formulations; ii) instead of balancing accuracy (quality) and diversity, only generating accurate results has been over emphasized. We therefore propose two new loss functions based on the Determinantal Point Process (DPP) likelihood, that can be adaptively applied to estimate the subsequent item or items. The DPP-distributed item set captures natural dependencies among temporal actions, and a quality vs. diversity decomposition of the DPP kernel pushes us to go beyond accuracy-oriented loss functions. Experimental results using the proposed loss functions on three real-world datasets show marked improvements over state-of-the-art sequential recommendation methods in both quality and diversity metrics.

Fair Wrapping for Black-box Predictions

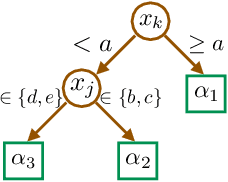
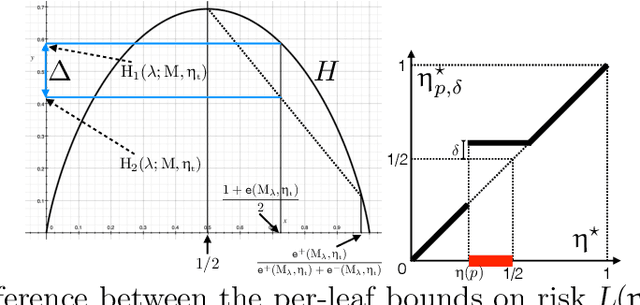
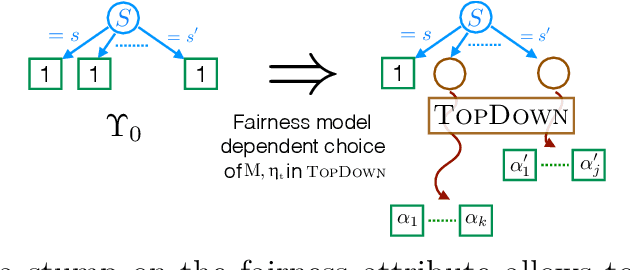
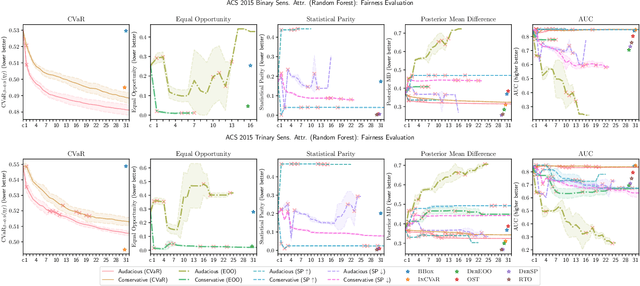
We introduce a new family of techniques to post-process ("wrap") a black-box classifier in order to reduce its bias. Our technique builds on the recent analysis of improper loss functions whose optimisation can correct any twist in prediction, unfairness being treated as a twist. In the post-processing, we learn a wrapper function which we define as an {\alpha}-tree, which modifies the prediction. We provide two generic boosting algorithms to learn {\alpha}-trees. We show that our modification has appealing properties in terms of composition of{\alpha}-trees, generalization, interpretability, and KL divergence between modified and original predictions. We exemplify the use of our technique in three fairness notions: conditional value at risk, equality of opportunity, and statistical parity; and provide experiments on several readily available datasets.

Factorized Fourier Neural Operators

The Fourier Neural Operator (FNO) is a learning-based method for efficiently simulating partial differential equations. We propose the Factorized Fourier Neural Operator (F-FNO) that allows much better generalization with deeper networks. With a careful combination of the Fourier factorization, a shared kernel integral operator across all layers, the Markov property, and residual connections, F-FNOs achieve a six-fold reduction in error on the most turbulent setting of the Navier-Stokes benchmark dataset. We show that our model maintains an error rate of 2% while still running an order of magnitude faster than a numerical solver, even when the problem setting is extended to include additional contexts such as viscosity and time-varying forces. This enables the same pretrained neural network to model vastly different conditions.

Interval-censored Hawkes processes

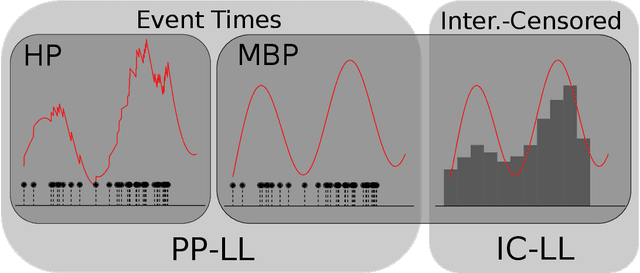
Hawkes processes are a popular means of modeling the event times of self-exciting phenomena, such as earthquake strikes or tweets on a topical subject. Classically, these models are fit to historical event time data via likelihood maximization. However, in many scenarios, the exact times of historical events are not recorded for either privacy (e.g., patient admittance to hospitals) or technical limitations (e.g., most transport data records the volume of vehicles passing loop detectors but not the individual times). The interval-censored setting denotes when only the aggregate counts of events at specific time intervals are observed. Fitting the parameters of interval-censored Hawkes processes requires designing new training objectives that do not rely on the exact event times. In this paper, we propose a model to estimate the parameters of a Hawkes process in interval-censored settings. Our model builds upon the existing Hawkes Intensity Process (HIP) of in several important directions. First, we observe that while HIP is formulated in terms of expected intensities, it is more natural to work instead with expected counts; further, one can express the latter as the solution to an integral equation closely related to the defining equation of HIP. Second, we show how a non-homogeneous Poisson approximation to the Hawkes process admits a tractable likelihood in the interval-censored setting; this approximation recovers the original HIP objective as a special case, and allows for the use of a broader class of Bregman divergences as loss function. Third, we explicate how to compute a tighter approximation to the ground truth in the likelihood. Finally, we show how our model can incorporate information about varying interval lengths. Experiments on synthetic and real-world data confirm our HIPPer model outperforms HIP and several other baselines on the task of interval-censored inference.

Radflow: A Recurrent, Aggregated, and Decomposable Model for Networks of Time Series

We propose a new model for networks of time series that influence each other. Graph structures among time series are found in diverse domains, such as web traffic influenced by hyperlinks, product sales influenced by recommendation, or urban transport volume influenced by road networks and weather. There has been recent progress in graph modeling and in time series forecasting, respectively, but an expressive and scalable approach for a network of series does not yet exist. We introduce Radflow, a novel model that embodies three key ideas: a recurrent neural network to obtain node embeddings that depend on time, the aggregation of the flow of influence from neighboring nodes with multi-head attention, and the multi-layer decomposition of time series. Radflow naturally takes into account dynamic networks where nodes and edges change over time, and it can be used for prediction and data imputation tasks. On real-world datasets ranging from a few hundred to a few hundred thousand nodes, we observe that Radflow variants are the best performing model across a wide range of settings. The recurrent component in Radflow also outperforms N-BEATS, the state-of-the-art time series model. We show that Radflow can learn different trends and seasonal patterns, that it is robust to missing nodes and edges, and that correlated temporal patterns among network neighbors reflect influence strength. We curate WikiTraffic, the largest dynamic network of time series with 366K nodes and 22M time-dependent links spanning five years. This dataset provides an open benchmark for developing models in this area, with applications that include optimizing resources for the web. More broadly, Radflow has the potential to improve forecasts in correlated time series networks such as the stock market, and impute missing measurements in geographically dispersed networks of natural phenomena.

AttentionFlow: Visualising Influence in Networks of Time Series

The collective attention on online items such as web pages, search terms, and videos reflects trends that are of social, cultural, and economic interest. Moreover, attention trends of different items exhibit mutual influence via mechanisms such as hyperlinks or recommendations. Many visualisation tools exist for time series, network evolution, or network influence; however, few systems connect all three. In this work, we present AttentionFlow, a new system to visualise networks of time series and the dynamic influence they have on one another. Centred around an ego node, our system simultaneously presents the time series on each node using two visual encodings: a tree ring for an overview and a line chart for details. AttentionFlow supports interactions such as overlaying time series of influence and filtering neighbours by time or flux. We demonstrate AttentionFlow using two real-world datasets, VevoMusic and WikiTraffic. We show that attention spikes in songs can be explained by external events such as major awards, or changes in the network such as the release of a new song. Separate case studies also demonstrate how an artist's influence changes over their career, and that correlated Wikipedia traffic is driven by cultural interests. More broadly, AttentionFlow can be generalised to visualise networks of time series on physical infrastructures such as road networks, or natural phenomena such as weather and geological measurements.

SupMMD: A Sentence Importance Model for Extractive Summarization using Maximum Mean Discrepancy

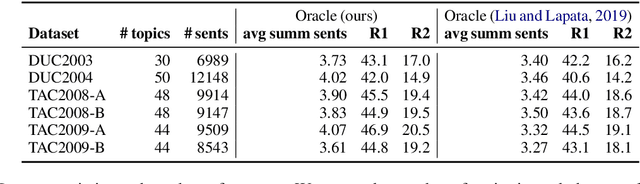
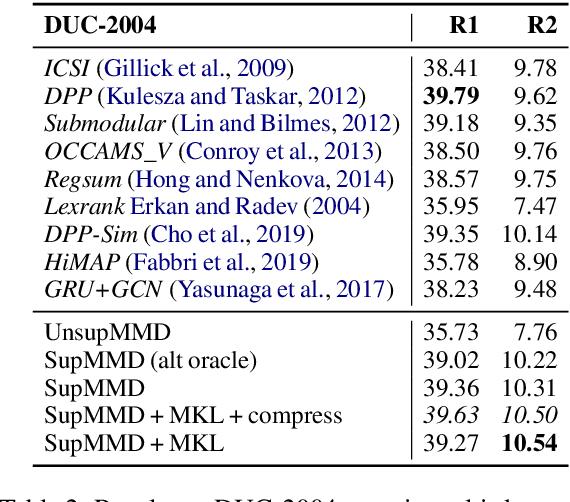
Most work on multi-document summarization has focused on generic summarization of information present in each individual document set. However, the under-explored setting of update summarization, where the goal is to identify the new information present in each set, is of equal practical interest (e.g., presenting readers with updates on an evolving news topic). In this work, we present SupMMD, a novel technique for generic and update summarization based on the maximum mean discrepancy from kernel two-sample testing. SupMMD combines both supervised learning for salience and unsupervised learning for coverage and diversity. Further, we adapt multiple kernel learning to make use of similarity across multiple information sources (e.g., text features and knowledge based concepts). We show the efficacy of SupMMD in both generic and update summarization tasks by meeting or exceeding the current state-of-the-art on the DUC-2004 and TAC-2009 datasets.