Leanne Dong
Interval-censored Hawkes processes
Apr 16, 2021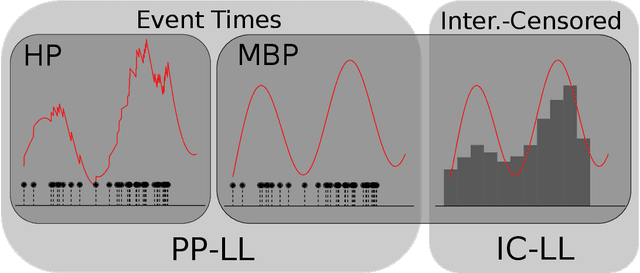



Abstract:Hawkes processes are a popular means of modeling the event times of self-exciting phenomena, such as earthquake strikes or tweets on a topical subject. Classically, these models are fit to historical event time data via likelihood maximization. However, in many scenarios, the exact times of historical events are not recorded for either privacy (e.g., patient admittance to hospitals) or technical limitations (e.g., most transport data records the volume of vehicles passing loop detectors but not the individual times). The interval-censored setting denotes when only the aggregate counts of events at specific time intervals are observed. Fitting the parameters of interval-censored Hawkes processes requires designing new training objectives that do not rely on the exact event times. In this paper, we propose a model to estimate the parameters of a Hawkes process in interval-censored settings. Our model builds upon the existing Hawkes Intensity Process (HIP) of in several important directions. First, we observe that while HIP is formulated in terms of expected intensities, it is more natural to work instead with expected counts; further, one can express the latter as the solution to an integral equation closely related to the defining equation of HIP. Second, we show how a non-homogeneous Poisson approximation to the Hawkes process admits a tractable likelihood in the interval-censored setting; this approximation recovers the original HIP objective as a special case, and allows for the use of a broader class of Bregman divergences as loss function. Third, we explicate how to compute a tighter approximation to the ground truth in the likelihood. Finally, we show how our model can incorporate information about varying interval lengths. Experiments on synthetic and real-world data confirm our HIPPer model outperforms HIP and several other baselines on the task of interval-censored inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge