A Generalization Bound for Nearly-Linear Networks

We consider nonlinear networks as perturbations of linear ones. Based on this approach, we present novel generalization bounds that become non-vacuous for networks that are close to being linear. The main advantage over the previous works which propose non-vacuous generalization bounds is that our bounds are a-priori: performing the actual training is not required for evaluating the bounds. To the best of our knowledge, they are the first non-vacuous generalization bounds for neural nets possessing this property.

Neural Tangent Kernel: A Survey

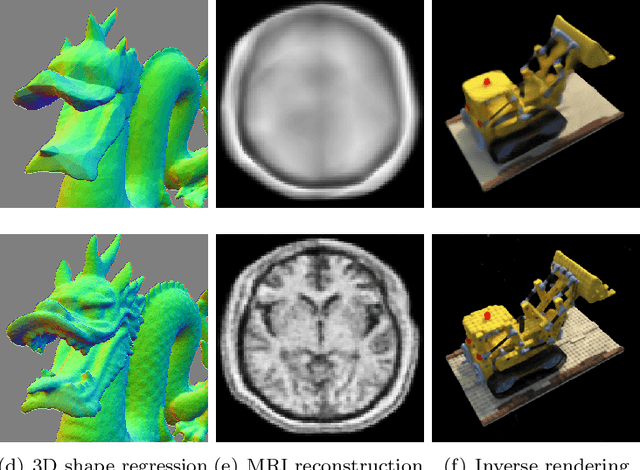
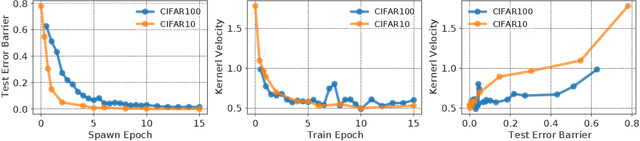
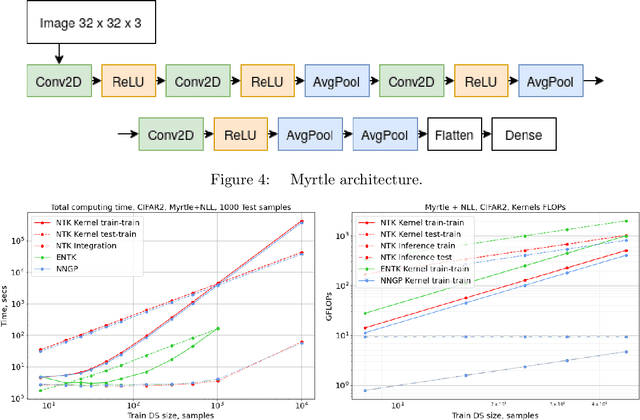
A seminal work [Jacot et al., 2018] demonstrated that training a neural network under specific parameterization is equivalent to performing a particular kernel method as width goes to infinity. This equivalence opened a promising direction for applying the results of the rich literature on kernel methods to neural nets which were much harder to tackle. The present survey covers key results on kernel convergence as width goes to infinity, finite-width corrections, applications, and a discussion of the limitations of the corresponding method.

Feature Learning in $L_{2}$-regularized DNNs: Attraction/Repulsion and Sparsity

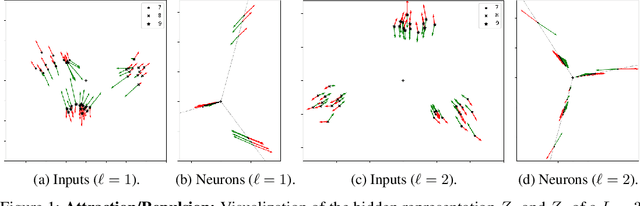
We study the loss surface of DNNs with $L_{2}$ regularization. We show that the loss in terms of the parameters can be reformulated into a loss in terms of the layerwise activations $Z_{\ell}$ of the training set. This reformulation reveals the dynamics behind feature learning: each hidden representations $Z_{\ell}$ are optimal w.r.t. to an attraction/repulsion problem and interpolate between the input and output representations, keeping as little information from the input as necessary to construct the activation of the next layer. For positively homogeneous non-linearities, the loss can be further reformulated in terms of the covariances of the hidden representations, which takes the form of a partially convex optimization over a convex cone. This second reformulation allows us to prove a sparsity result for homogeneous DNNs: any local minimum of the $L_{2}$-regularized loss can be achieved with at most $N(N+1)$ neurons in each hidden layer (where $N$ is the size of the training set). We show that this bound is tight by giving an example of a local minimum which requires $N^{2}/4$ hidden neurons. But we also observe numerically that in more traditional settings much less than $N^{2}$ neurons are required to reach the minima.

An Essay on Optimization Mystery of Deep Learning

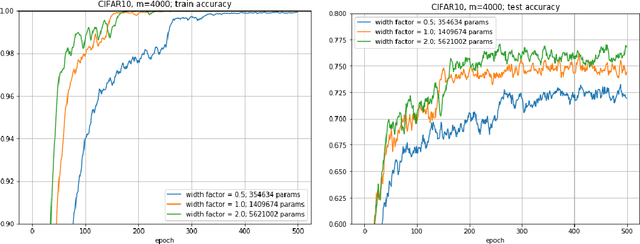
Despite the huge empirical success of deep learning, theoretical understanding of neural networks learning process is still lacking. This is the reason, why some of its features seem "mysterious". We emphasize two mysteries of deep learning: generalization mystery, and optimization mystery. In this essay we review and draw connections between several selected works concerning the latter.

Embedding-reparameterization procedure for manifold-valued latent variables in generative models

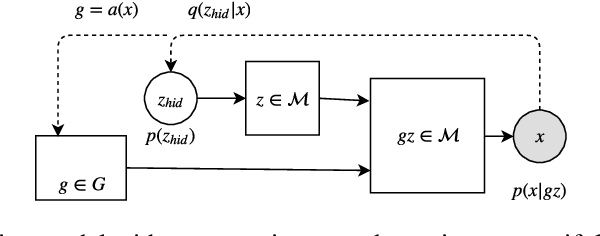
Conventional prior for Variational Auto-Encoder (VAE) is a Gaussian distribution. Recent works demonstrated that choice of prior distribution affects learning capacity of VAE models. We propose a general technique (embedding-reparameterization procedure, or ER) for introducing arbitrary manifold-valued variables in VAE model. We compare our technique with a conventional VAE on a toy benchmark problem. This is work in progress.

Differentiable lower bound for expected BLEU score

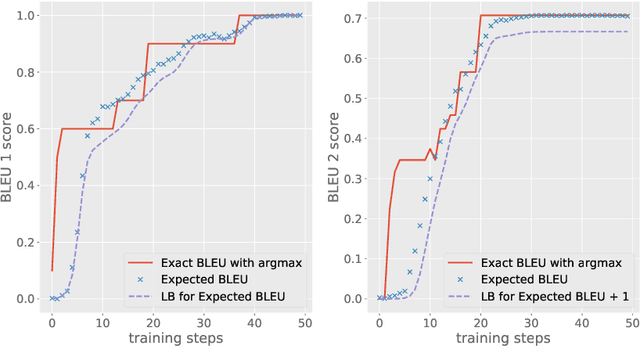
In natural language processing tasks performance of the models is often measured with some non-differentiable metric, such as BLEU score. To use efficient gradient-based methods for optimization, it is a common workaround to optimize some surrogate loss function. This approach is effective if optimization of such loss also results in improving target metric. The corresponding problem is referred to as loss-evaluation mismatch. In the present work we propose a method for calculation of differentiable lower bound of expected BLEU score that does not involve computationally expensive sampling procedure such as the one required when using REINFORCE rule from reinforcement learning (RL) framework.

Using stochastic computation graphs formalism for optimization of sequence-to-sequence model

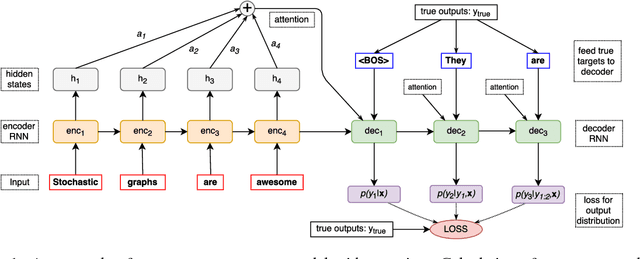
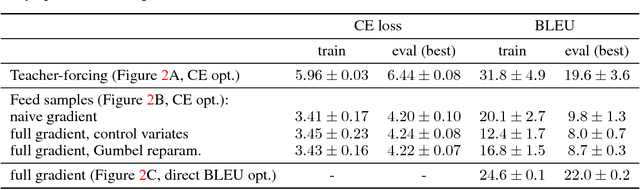
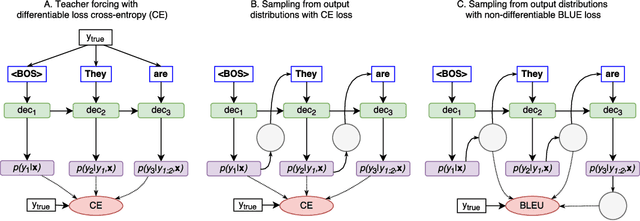
Variety of machine learning problems can be formulated as an optimization task for some (surrogate) loss function. Calculation of loss function can be viewed in terms of stochastic computation graphs (SCG). We use this formalism to analyze a problem of optimization of famous sequence-to-sequence model with attention and propose reformulation of the task. Examples are given for machine translation (MT). Our work provides a unified view on different optimization approaches for sequence-to-sequence models and could help researchers in developing new network architectures with embedded stochastic nodes.