Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Eduard Pokonechnyy
Neural Tangent Kernel: A Survey
Aug 29, 2022Figures and Tables:
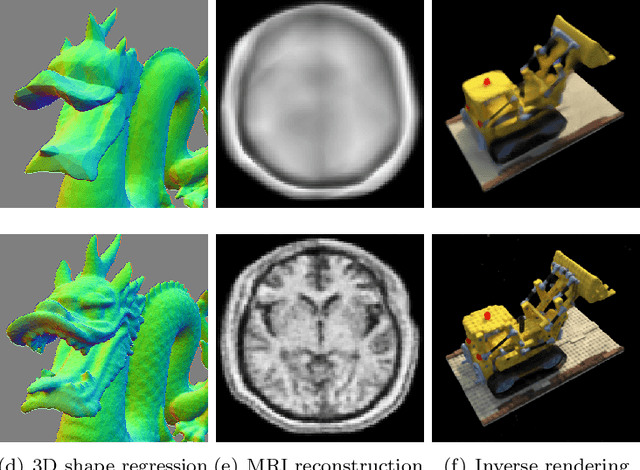
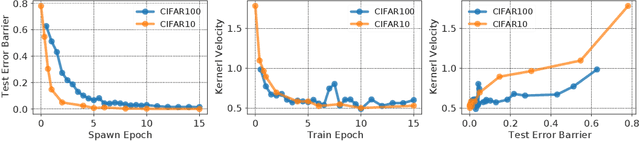
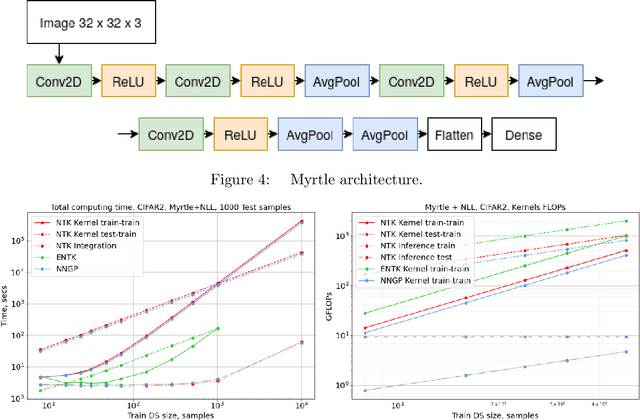




Abstract:A seminal work [Jacot et al., 2018] demonstrated that training a neural network under specific parameterization is equivalent to performing a particular kernel method as width goes to infinity. This equivalence opened a promising direction for applying the results of the rich literature on kernel methods to neural nets which were much harder to tackle. The present survey covers key results on kernel convergence as width goes to infinity, finite-width corrections, applications, and a discussion of the limitations of the corresponding method.
* 47 pages, 8 figures
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge