Geometry of the Loss Landscape in Overparameterized Neural Networks: Symmetries and Invariances

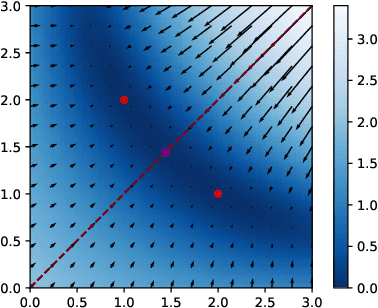
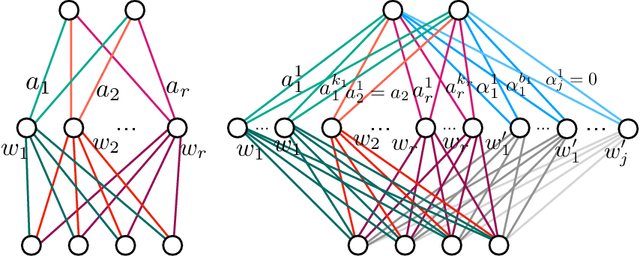
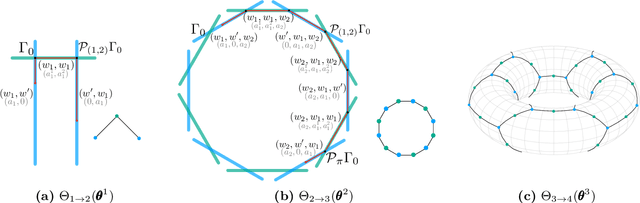
We study how permutation symmetries in overparameterized multi-layer neural networks generate `symmetry-induced' critical points. Assuming a network with $ L $ layers of minimal widths $ r_1^*, \ldots, r_{L-1}^* $ reaches a zero-loss minimum at $ r_1^*! \cdots r_{L-1}^*! $ isolated points that are permutations of one another, we show that adding one extra neuron to each layer is sufficient to connect all these previously discrete minima into a single manifold. For a two-layer overparameterized network of width $ r^*+ h =: m $ we explicitly describe the manifold of global minima: it consists of $ T(r^*, m) $ affine subspaces of dimension at least $ h $ that are connected to one another. For a network of width $m$, we identify the number $G(r,m)$ of affine subspaces containing only symmetry-induced critical points that are related to the critical points of a smaller network of width $r<r^*$. Via a combinatorial analysis, we derive closed-form formulas for $ T $ and $ G $ and show that the number of symmetry-induced critical subspaces dominates the number of affine subspaces forming the global minima manifold in the mildly overparameterized regime (small $ h $) and vice versa in the vastly overparameterized regime ($h \gg r^*$). Our results provide new insights into the minimization of the non-convex loss function of overparameterized neural networks.

Kernel Alignment Risk Estimator: Risk Prediction from Training Data

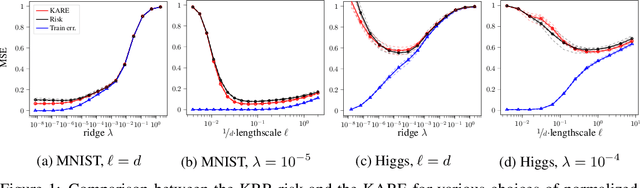
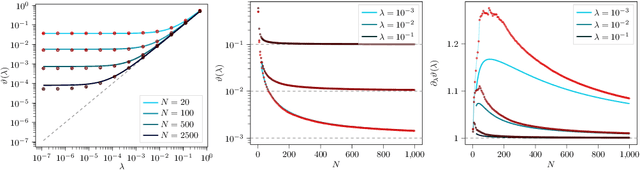
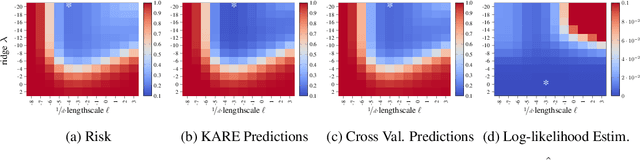
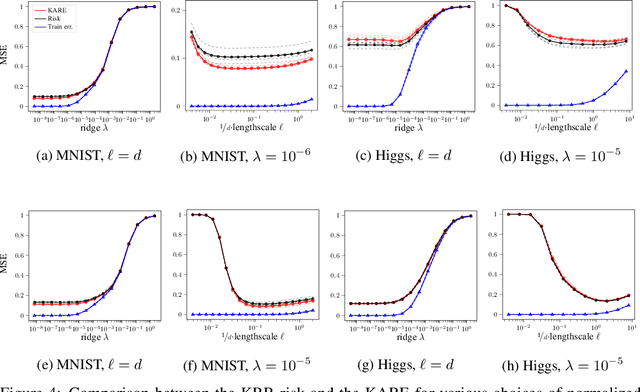
We study the risk (i.e. generalization error) of Kernel Ridge Regression (KRR) for a kernel $K$ with ridge $\lambda>0$ and i.i.d. observations. For this, we introduce two objects: the Signal Capture Threshold (SCT) and the Kernel Alignment Risk Estimator (KARE). The SCT $\vartheta_{K,\lambda}$ is a function of the data distribution: it can be used to identify the components of the data that the KRR predictor captures, and to approximate the (expected) KRR risk. This then leads to a KRR risk approximation by the KARE $\rho_{K, \lambda}$, an explicit function of the training data, agnostic of the true data distribution. We phrase the regression problem in a functional setting. The key results then follow from a finite-size analysis of the Stieltjes transform of general Wishart random matrices. Under a natural universality assumption (that the KRR moments depend asymptotically on the first two moments of the observations) we capture the mean and variance of the KRR predictor. We numerically investigate our findings on the Higgs and MNIST datasets for various classical kernels: the KARE gives an excellent approximation of the risk, thus supporting our universality assumption. Using the KARE, one can compare choices of Kernels and hyperparameters directly from the training set. The KARE thus provides a promising data-dependent procedure to select Kernels that generalize well.

Implicit Regularization of Random Feature Models

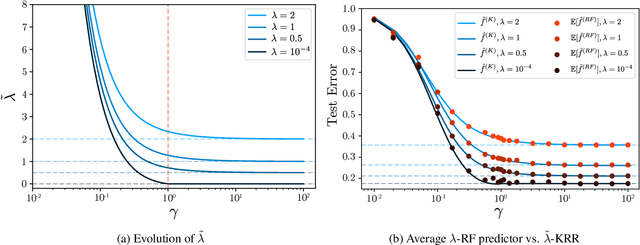
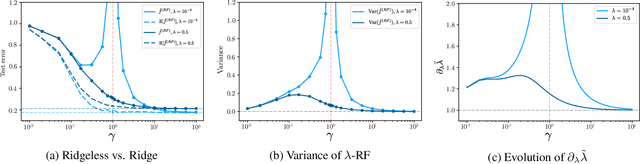
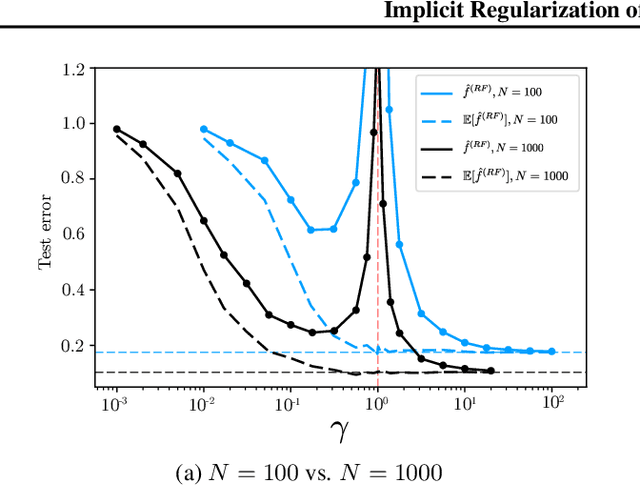
Random Feature (RF) models are used as efficient parametric approximations of kernel methods. We investigate, by means of random matrix theory, the connection between Gaussian RF models and Kernel Ridge Regression (KRR). For a Gaussian RF model with $P$ features, $N$ data points, and a ridge $\lambda$, we show that the average (i.e. expected) RF predictor is close to a KRR predictor with an effective ridge $\tilde{\lambda}$. We show that $\tilde{\lambda} > \lambda$ and $\tilde{\lambda} \searrow \lambda$ monotonically as $P$ grows, thus revealing the implicit regularization effect of finite RF sampling. We then compare the risk (i.e. test error) of the $\tilde{\lambda}$-KRR predictor with the average risk of the $\lambda$-RF predictor and obtain a precise and explicit bound on their difference. Finally, we empirically find an extremely good agreement between the test errors of the average $\lambda$-RF predictor and $\tilde{\lambda}$-KRR predictor.