Should Under-parameterized Student Networks Copy or Average Teacher Weights?

Any continuous function $f^*$ can be approximated arbitrarily well by a neural network with sufficiently many neurons $k$. We consider the case when $f^*$ itself is a neural network with one hidden layer and $k$ neurons. Approximating $f^*$ with a neural network with $n< k$ neurons can thus be seen as fitting an under-parameterized "student" network with $n$ neurons to a "teacher" network with $k$ neurons. As the student has fewer neurons than the teacher, it is unclear, whether each of the $n$ student neurons should copy one of the teacher neurons or rather average a group of teacher neurons. For shallow neural networks with erf activation function and for the standard Gaussian input distribution, we prove that "copy-average" configurations are critical points if the teacher's incoming vectors are orthonormal and its outgoing weights are unitary. Moreover, the optimum among such configurations is reached when $n-1$ student neurons each copy one teacher neuron and the $n$-th student neuron averages the remaining $k-n+1$ teacher neurons. For the student network with $n=1$ neuron, we provide additionally a closed-form solution of the non-trivial critical point(s) for commonly used activation functions through solving an equivalent constrained optimization problem. Empirically, we find for the erf activation function that gradient flow converges either to the optimal copy-average critical point or to another point where each student neuron approximately copies a different teacher neuron. Finally, we find similar results for the ReLU activation function, suggesting that the optimal solution of underparameterized networks has a universal structure.

Are training trajectories of deep single-spike and deep ReLU network equivalent?

Communication by binary and sparse spikes is a key factor for the energy efficiency of biological brains. However, training deep spiking neural networks (SNNs) with backpropagation is harder than with artificial neural networks (ANNs), which is puzzling given that recent theoretical results provide exact mapping algorithms from ReLU to time-to-first-spike (TTFS) SNNs. Building upon these results, we analyze in theory and in simulation the learning dynamics of TTFS-SNNs. Our analysis highlights that even when an SNN can be mapped exactly to a ReLU network, it cannot always be robustly trained by gradient descent. The reason for that is the emergence of a specific instance of the vanishing-or-exploding gradient problem leading to a bias in the gradient descent trajectory in comparison with the equivalent ANN. After identifying this issue we derive a generic solution for the network initialization and SNN parameterization which guarantees that the SNN can be trained as robustly as its ANN counterpart. Our theoretical findings are illustrated in practice on image classification datasets. Our method achieves the same accuracy as deep ConvNets on CIFAR10 and enables fine-tuning on the much larger PLACES365 dataset without loss of accuracy compared to the ANN. We argue that the combined perspective of conversion and fine-tuning with robust gradient descent in SNN will be decisive to optimize SNNs for hardware implementations needing low latency and resilience to noise and quantization.

GateON: an unsupervised method for large scale continual learning

The objective of continual learning (CL) is to learn tasks sequentially without retraining on earlier tasks. However, when subjected to CL, traditional neural networks exhibit catastrophic forgetting and limited generalization. To overcome these problems, we introduce a novel method called 'Gate and Obstruct Network' (GateON). GateON combines learnable gating of activity and online estimation of parameter relevance to safeguard crucial knowledge from being overwritten. Our method generates partially overlapping pathways between tasks which permits forward and backward transfer during sequential learning. GateON addresses the issue of network saturation after parameter fixation by a re-activation mechanism of fixed neurons, enabling large-scale continual learning. GateON is implemented on a wide range of networks (fully-connected, CNN, Transformers), has low computational complexity, effectively learns up to 100 MNIST learning tasks, and achieves top-tier results for pre-trained BERT in CL-based NLP tasks.

Expand-and-Cluster: Exact Parameter Recovery of Neural Networks

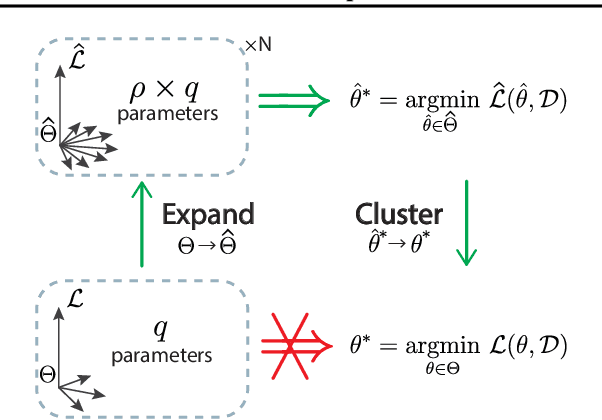
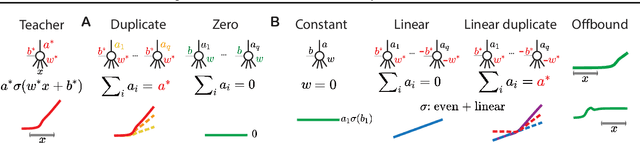
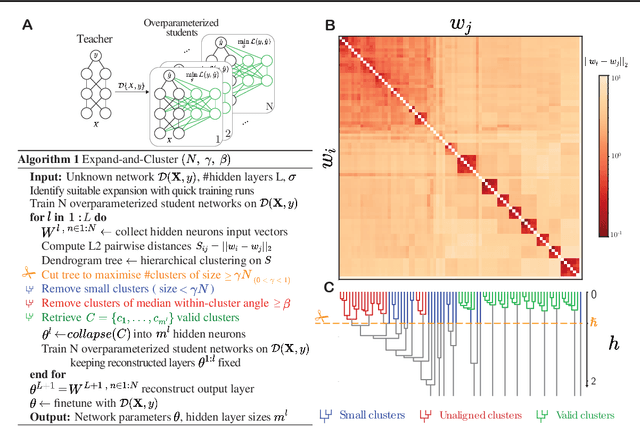
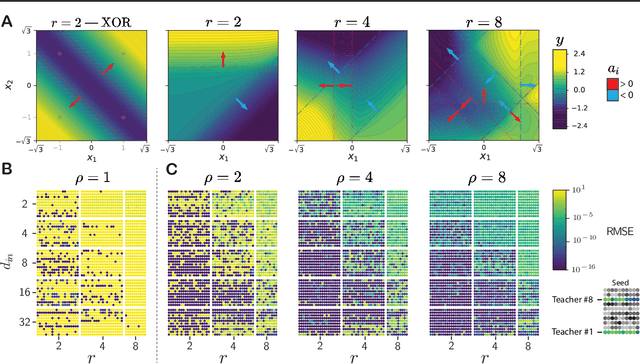
Can we recover the hidden parameters of an Artificial Neural Network (ANN) by probing its input-output mapping? We propose a systematic method, called `Expand-and-Cluster' that needs only the number of hidden layers and the activation function of the probed ANN to identify all network parameters. In the expansion phase, we train a series of student networks of increasing size using the probed data of the ANN as a teacher. Expansion stops when a minimal loss is consistently reached in student networks of a given size. In the clustering phase, weight vectors of the expanded students are clustered, which allows structured pruning of superfluous neurons in a principled way. We find that an overparameterization of a factor four is sufficient to reliably identify the minimal number of neurons and to retrieve the original network parameters in $80\%$ of tasks across a family of 150 toy problems of variable difficulty. Furthermore, a teacher network trained on MNIST data can be identified with less than $5\%$ overhead in the neuron number. Thus, while direct training of a student network with a size identical to that of the teacher is practically impossible because of the non-convex loss function, training with mild overparameterization followed by clustering and structured pruning correctly identifies the target network.

MLPGradientFlow: going with the flow of multilayer perceptrons (and finding minima fast and accurately)

MLPGradientFlow is a software package to solve numerically the gradient flow differential equation $\dot \theta = -\nabla \mathcal L(\theta; \mathcal D)$, where $\theta$ are the parameters of a multi-layer perceptron, $\mathcal D$ is some data set, and $\nabla \mathcal L$ is the gradient of a loss function. We show numerically that adaptive first- or higher-order integration methods based on Runge-Kutta schemes have better accuracy and convergence speed than gradient descent with the Adam optimizer. However, we find Newton's method and approximations like BFGS preferable to find fixed points (local and global minima of $\mathcal L$) efficiently and accurately. For small networks and data sets, gradients are usually computed faster than in pytorch and Hessian are computed at least $5\times$ faster. Additionally, the package features an integrator for a teacher-student setup with bias-free, two-layer networks trained with standard Gaussian input in the limit of infinite data. The code is accessible at https://github.com/jbrea/MLPGradientFlow.jl.

An Exact Mapping From ReLU Networks to Spiking Neural Networks

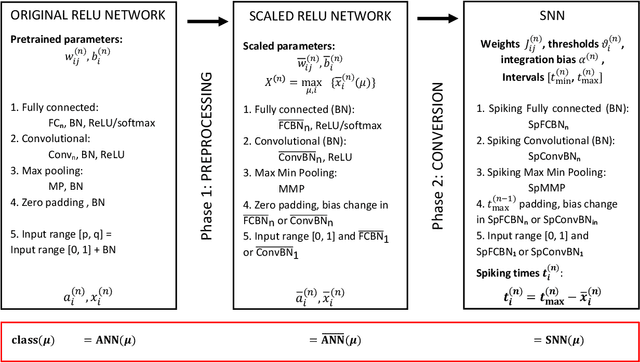
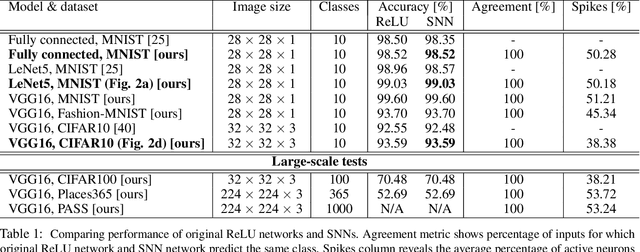
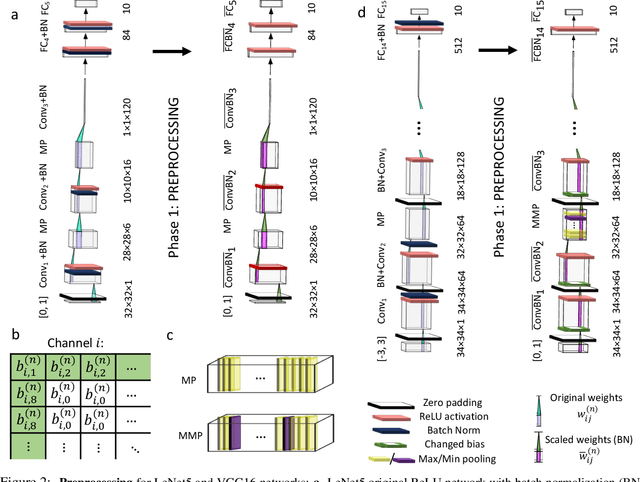
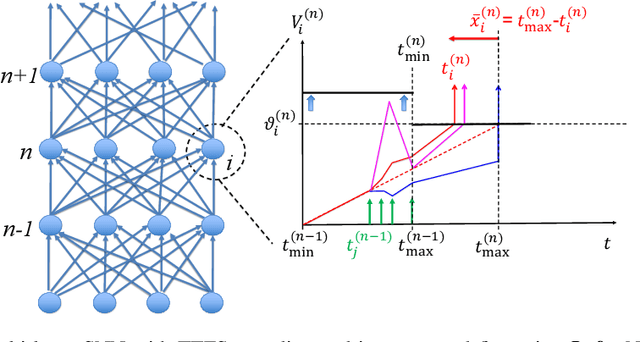
Deep spiking neural networks (SNNs) offer the promise of low-power artificial intelligence. However, training deep SNNs from scratch or converting deep artificial neural networks to SNNs without loss of performance has been a challenge. Here we propose an exact mapping from a network with Rectified Linear Units (ReLUs) to an SNN that fires exactly one spike per neuron. For our constructive proof, we assume that an arbitrary multi-layer ReLU network with or without convolutional layers, batch normalization and max pooling layers was trained to high performance on some training set. Furthermore, we assume that we have access to a representative example of input data used during training and to the exact parameters (weights and biases) of the trained ReLU network. The mapping from deep ReLU networks to SNNs causes zero percent drop in accuracy on CIFAR10, CIFAR100 and the ImageNet-like data sets Places365 and PASS. More generally our work shows that an arbitrary deep ReLU network can be replaced by an energy-efficient single-spike neural network without any loss of performance.

A taxonomy of surprise definitions

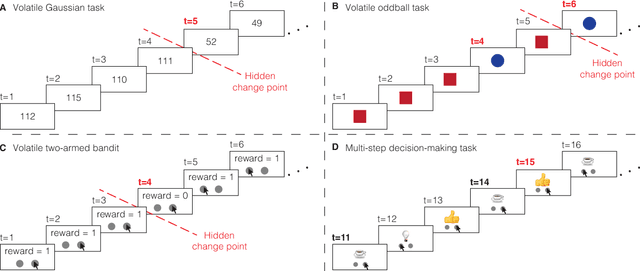
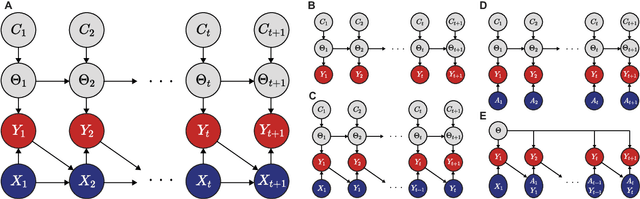
Surprising events trigger measurable brain activity and influence human behavior by affecting learning, memory, and decision-making. Currently there is, however, no consensus on the definition of surprise. Here we identify 18 mathematical definitions of surprise in a unifying framework. We first propose a technical classification of these definitions into three groups based on their dependence on an agent's belief, show how they relate to each other, and prove under what conditions they are indistinguishable. Going beyond this technical analysis, we propose a taxonomy of surprise definitions and classify them into four conceptual categories based on the quantity they measure: (i) 'prediction surprise' measures a mismatch between a prediction and an observation; (ii) 'change-point detection surprise' measures the probability of a change in the environment; (iii) 'confidence-corrected surprise' explicitly accounts for the effect of confidence; and (iv) 'information gain surprise' measures the belief-update upon a new observation. The taxonomy poses the foundation for principled studies of the functional roles and physiological signatures of surprise in the brain.

Kernel Memory Networks: A Unifying Framework for Memory Modeling

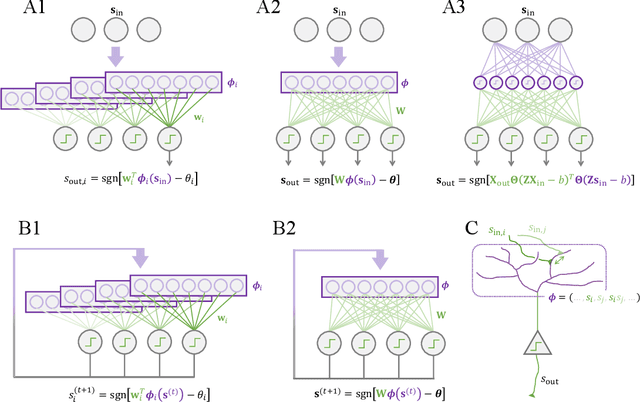
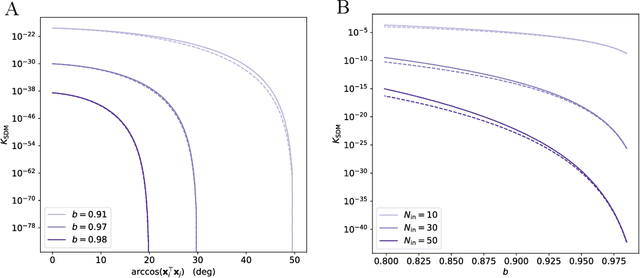
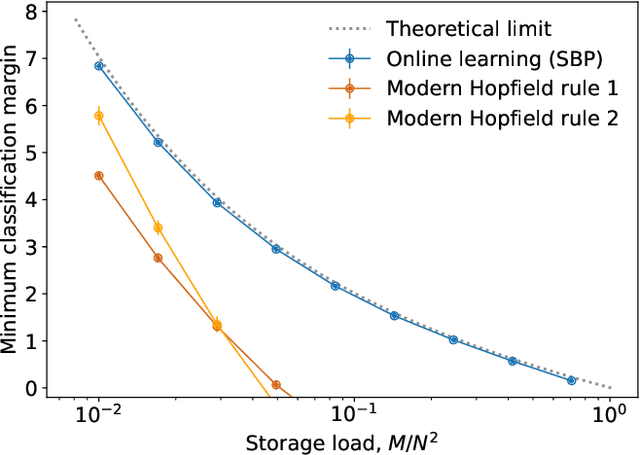
We consider the problem of training a neural network to store a set of patterns with maximal noise robustness. A solution, in terms of optimal weights and state update rules, is derived by training each individual neuron to perform either kernel classification or interpolation with a minimum weight norm. By applying this method to feed-forward and recurrent networks, we derive optimal networks that include, as special cases, many of the hetero- and auto-associative memory models that have been proposed over the past years, such as modern Hopfield networks and Kanerva's sparse distributed memory. We generalize Kanerva's model and demonstrate a simple way to design a kernel memory network that can store an exponential number of continuous-valued patterns with a finite basin of attraction. The framework of kernel memory networks offers a simple and intuitive way to understand the storage capacity of previous memory models, and allows for new biological interpretations in terms of dendritic non-linearities and synaptic clustering.

Mesoscopic modeling of hidden spiking neurons

Can we use spiking neural networks (SNN) as generative models of multi-neuronal recordings, while taking into account that most neurons are unobserved? Modeling the unobserved neurons with large pools of hidden spiking neurons leads to severely underconstrained problems that are hard to tackle with maximum likelihood estimation. In this work, we use coarse-graining and mean-field approximations to derive a bottom-up, neuronally-grounded latent variable model (neuLVM), where the activity of the unobserved neurons is reduced to a low-dimensional mesoscopic description. In contrast to previous latent variable models, neuLVM can be explicitly mapped to a recurrent, multi-population SNN, giving it a transparent biological interpretation. We show, on synthetic spike trains, that a few observed neurons are sufficient for neuLVM to perform efficient model inversion of large SNNs, in the sense that it can recover connectivity parameters, infer single-trial latent population activity, reproduce ongoing metastable dynamics, and generalize when subjected to perturbations mimicking photo-stimulation.

Fitting summary statistics of neural data with a differentiable spiking network simulator

Fitting network models to neural activity is becoming an important tool in neuroscience. A popular approach is to model a brain area with a probabilistic recurrent spiking network whose parameters maximize the likelihood of the recorded activity. Although this is widely used, we show that the resulting model does not produce realistic neural activity and wrongly estimates the connectivity matrix when neurons that are not recorded have a substantial impact on the recorded network. To correct for this, we suggest to augment the log-likelihood with terms that measure the dissimilarity between simulated and recorded activity. This dissimilarity is defined via summary statistics commonly used in neuroscience, and the optimization is efficient because it relies on back-propagation through the stochastically simulated spike trains. We analyze this method theoretically and show empirically that it generates more realistic activity statistics and recovers the connectivity matrix better than other methods.