Centaur: a foundation model of human cognition

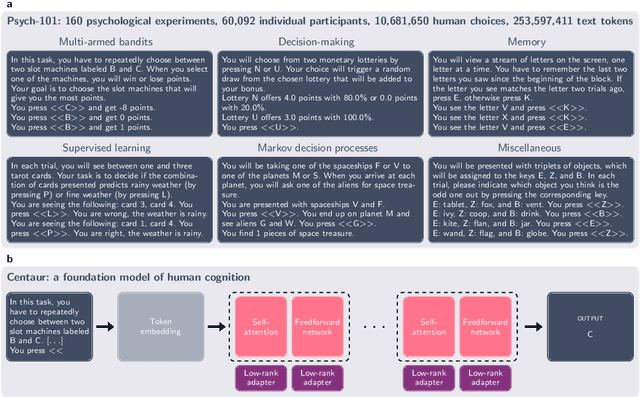
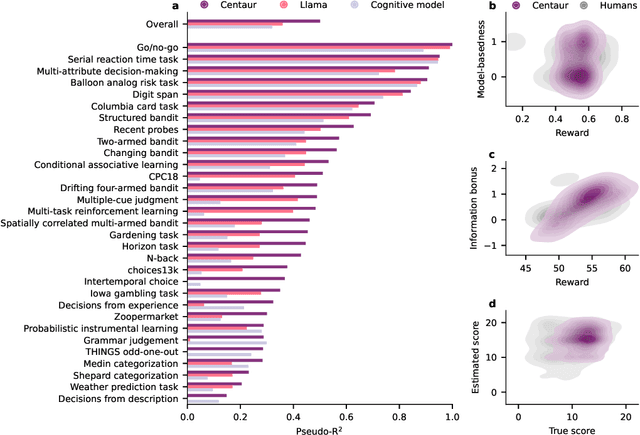
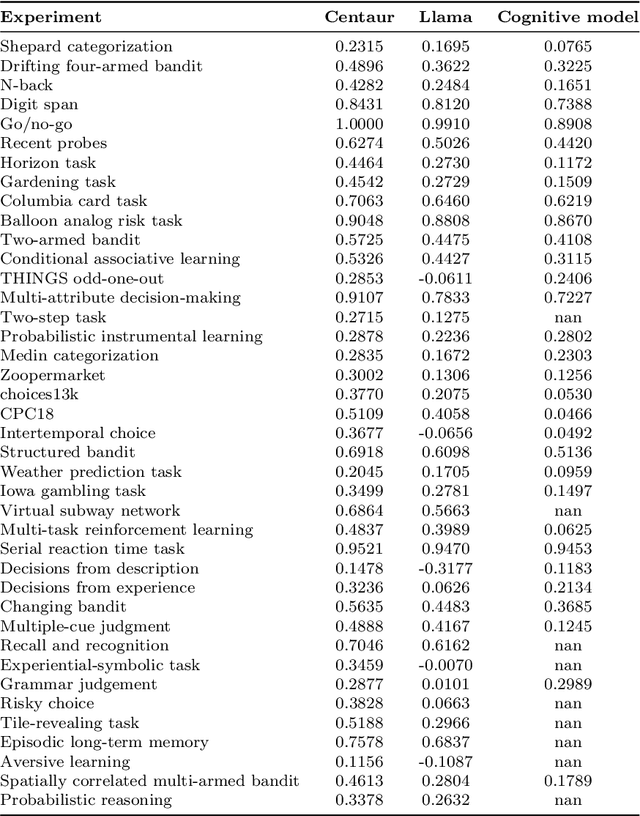
Establishing a unified theory of cognition has been a major goal of psychology. While there have been previous attempts to instantiate such theories by building computational models, we currently do not have one model that captures the human mind in its entirety. Here we introduce Centaur, a computational model that can predict and simulate human behavior in any experiment expressible in natural language. We derived Centaur by finetuning a state-of-the-art language model on a novel, large-scale data set called Psych-101. Psych-101 reaches an unprecedented scale, covering trial-by-trial data from over 60,000 participants performing over 10,000,000 choices in 160 experiments. Centaur not only captures the behavior of held-out participants better than existing cognitive models, but also generalizes to new cover stories, structural task modifications, and entirely new domains. Furthermore, we find that the model's internal representations become more aligned with human neural activity after finetuning. Taken together, Centaur is the first real candidate for a unified model of human cognition. We anticipate that it will have a disruptive impact on the cognitive sciences, challenging the existing paradigm for developing computational models.

A taxonomy of surprise definitions

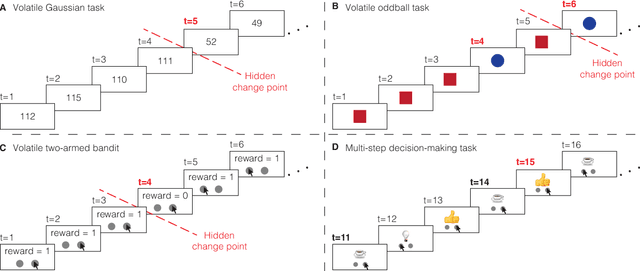
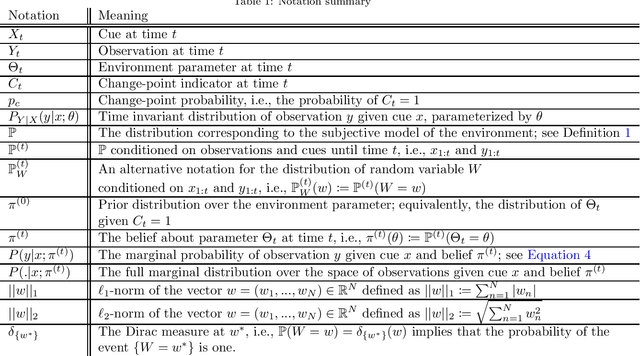
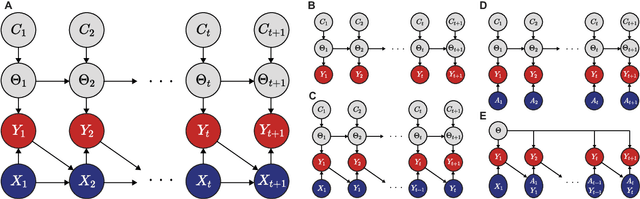
Surprising events trigger measurable brain activity and influence human behavior by affecting learning, memory, and decision-making. Currently there is, however, no consensus on the definition of surprise. Here we identify 18 mathematical definitions of surprise in a unifying framework. We first propose a technical classification of these definitions into three groups based on their dependence on an agent's belief, show how they relate to each other, and prove under what conditions they are indistinguishable. Going beyond this technical analysis, we propose a taxonomy of surprise definitions and classify them into four conceptual categories based on the quantity they measure: (i) 'prediction surprise' measures a mismatch between a prediction and an observation; (ii) 'change-point detection surprise' measures the probability of a change in the environment; (iii) 'confidence-corrected surprise' explicitly accounts for the effect of confidence; and (iv) 'information gain surprise' measures the belief-update upon a new observation. The taxonomy poses the foundation for principled studies of the functional roles and physiological signatures of surprise in the brain.

Fitting summary statistics of neural data with a differentiable spiking network simulator

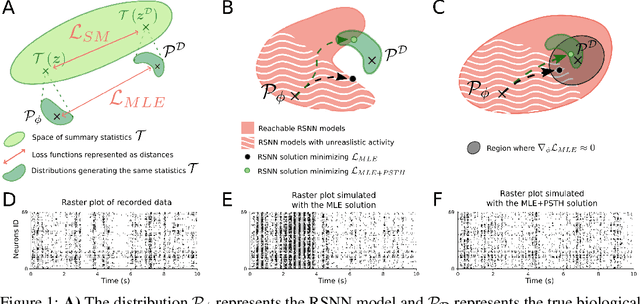
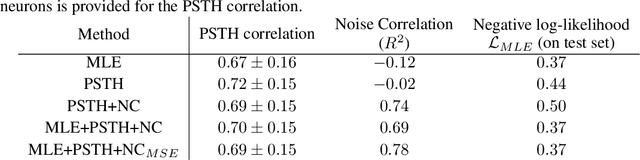
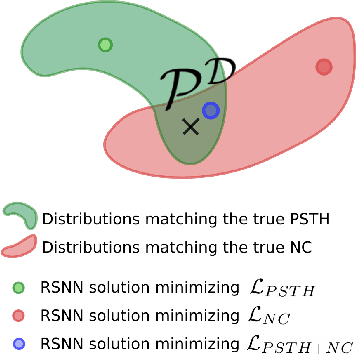
Fitting network models to neural activity is becoming an important tool in neuroscience. A popular approach is to model a brain area with a probabilistic recurrent spiking network whose parameters maximize the likelihood of the recorded activity. Although this is widely used, we show that the resulting model does not produce realistic neural activity and wrongly estimates the connectivity matrix when neurons that are not recorded have a substantial impact on the recorded network. To correct for this, we suggest to augment the log-likelihood with terms that measure the dissimilarity between simulated and recorded activity. This dissimilarity is defined via summary statistics commonly used in neuroscience, and the optimization is efficient because it relies on back-propagation through the stochastically simulated spike trains. We analyze this method theoretically and show empirically that it generates more realistic activity statistics and recovers the connectivity matrix better than other methods.

An Approximate Bayesian Approach to Surprise-Based Learning

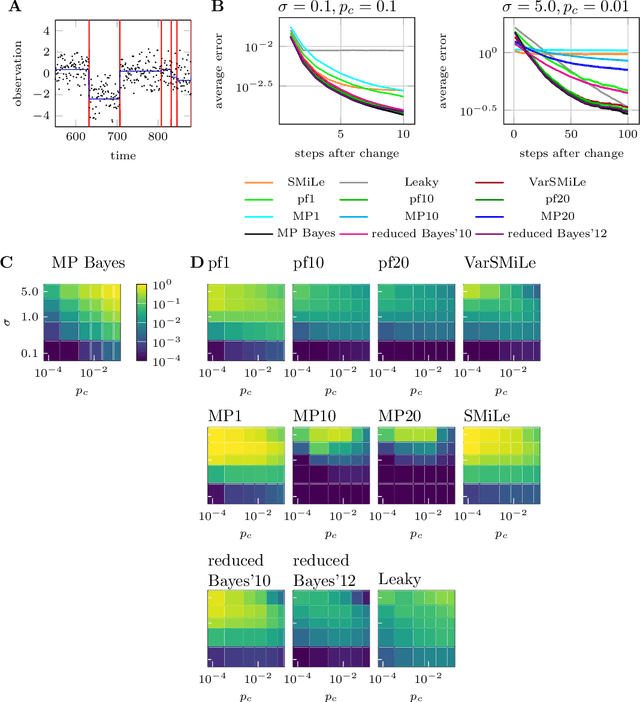
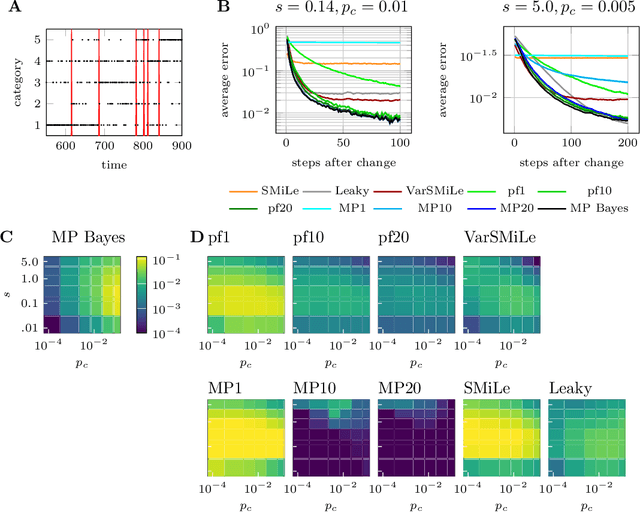
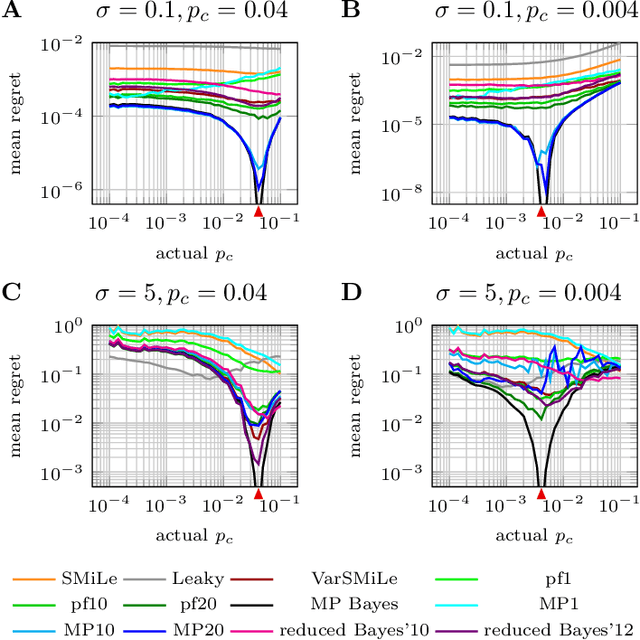
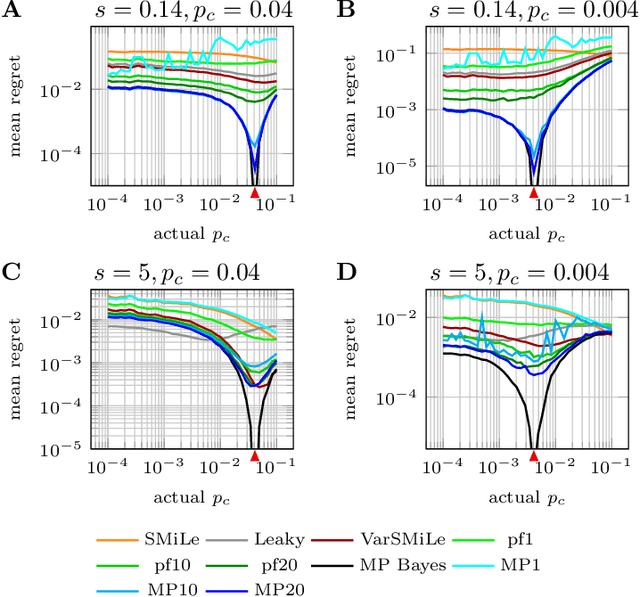
Surprise-based learning allows agents to adapt quickly in non-stationary stochastic environments. Most existing approaches to surprise-based learning and change point detection assume either implicitly or explicitly a simple, hierarchical generative model of observation sequences that are characterized by stationary periods separated by sudden changes. In this work we show that exact Bayesian inference gives naturally rise to a surprise-modulated trade-off between forgetting and integrating the new observations with the current belief. We demonstrate that many existing approximate Bayesian approaches also show surprise-based modulation of learning rates, and we derive novel particle filters and variational filters with update rules that exhibit surprise-based modulation. Our derived filters have a constant scaling in observation sequence length and particularly simple update dynamics for any distribution in the exponential family. Empirical results show that these filters estimate parameters better than alternative approximate approaches and reach comparative levels of performance to computationally more expensive algorithms. The theoretical insight of casting various approaches under the same interpretation of surprise-based learning, as well as the proposed filters, may find useful applications in reinforcement learning in non-stationary environments and in the analysis of animal and human behavior.