Should Under-parameterized Student Networks Copy or Average Teacher Weights?

Any continuous function $f^*$ can be approximated arbitrarily well by a neural network with sufficiently many neurons $k$. We consider the case when $f^*$ itself is a neural network with one hidden layer and $k$ neurons. Approximating $f^*$ with a neural network with $n< k$ neurons can thus be seen as fitting an under-parameterized "student" network with $n$ neurons to a "teacher" network with $k$ neurons. As the student has fewer neurons than the teacher, it is unclear, whether each of the $n$ student neurons should copy one of the teacher neurons or rather average a group of teacher neurons. For shallow neural networks with erf activation function and for the standard Gaussian input distribution, we prove that "copy-average" configurations are critical points if the teacher's incoming vectors are orthonormal and its outgoing weights are unitary. Moreover, the optimum among such configurations is reached when $n-1$ student neurons each copy one teacher neuron and the $n$-th student neuron averages the remaining $k-n+1$ teacher neurons. For the student network with $n=1$ neuron, we provide additionally a closed-form solution of the non-trivial critical point(s) for commonly used activation functions through solving an equivalent constrained optimization problem. Empirically, we find for the erf activation function that gradient flow converges either to the optimal copy-average critical point or to another point where each student neuron approximately copies a different teacher neuron. Finally, we find similar results for the ReLU activation function, suggesting that the optimal solution of underparameterized networks has a universal structure.

Expand-and-Cluster: Exact Parameter Recovery of Neural Networks

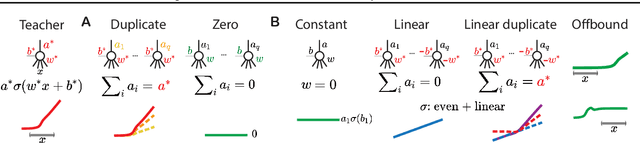
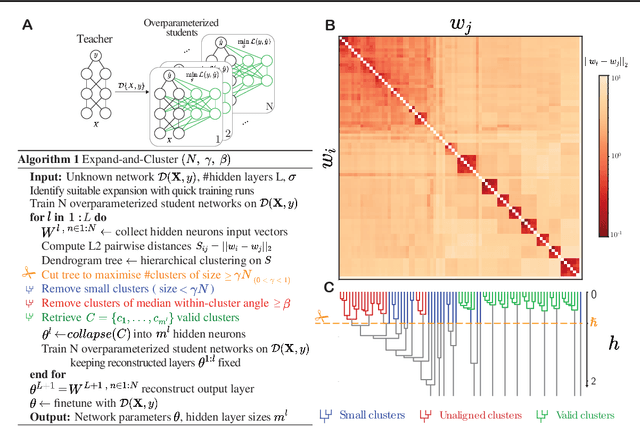
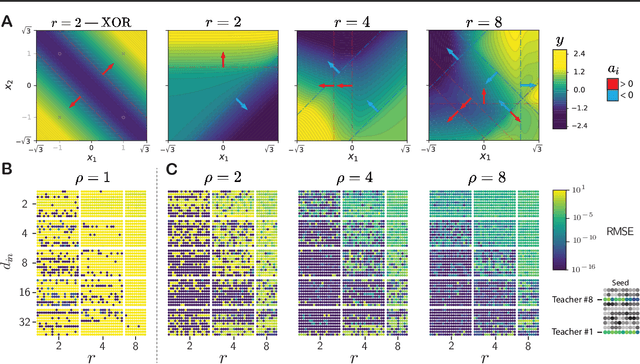
Can we recover the hidden parameters of an Artificial Neural Network (ANN) by probing its input-output mapping? We propose a systematic method, called `Expand-and-Cluster' that needs only the number of hidden layers and the activation function of the probed ANN to identify all network parameters. In the expansion phase, we train a series of student networks of increasing size using the probed data of the ANN as a teacher. Expansion stops when a minimal loss is consistently reached in student networks of a given size. In the clustering phase, weight vectors of the expanded students are clustered, which allows structured pruning of superfluous neurons in a principled way. We find that an overparameterization of a factor four is sufficient to reliably identify the minimal number of neurons and to retrieve the original network parameters in $80\%$ of tasks across a family of 150 toy problems of variable difficulty. Furthermore, a teacher network trained on MNIST data can be identified with less than $5\%$ overhead in the neuron number. Thus, while direct training of a student network with a size identical to that of the teacher is practically impossible because of the non-convex loss function, training with mild overparameterization followed by clustering and structured pruning correctly identifies the target network.

MLPGradientFlow: going with the flow of multilayer perceptrons (and finding minima fast and accurately)

MLPGradientFlow is a software package to solve numerically the gradient flow differential equation $\dot \theta = -\nabla \mathcal L(\theta; \mathcal D)$, where $\theta$ are the parameters of a multi-layer perceptron, $\mathcal D$ is some data set, and $\nabla \mathcal L$ is the gradient of a loss function. We show numerically that adaptive first- or higher-order integration methods based on Runge-Kutta schemes have better accuracy and convergence speed than gradient descent with the Adam optimizer. However, we find Newton's method and approximations like BFGS preferable to find fixed points (local and global minima of $\mathcal L$) efficiently and accurately. For small networks and data sets, gradients are usually computed faster than in pytorch and Hessian are computed at least $5\times$ faster. Additionally, the package features an integrator for a teacher-student setup with bias-free, two-layer networks trained with standard Gaussian input in the limit of infinite data. The code is accessible at https://github.com/jbrea/MLPGradientFlow.jl.

A taxonomy of surprise definitions

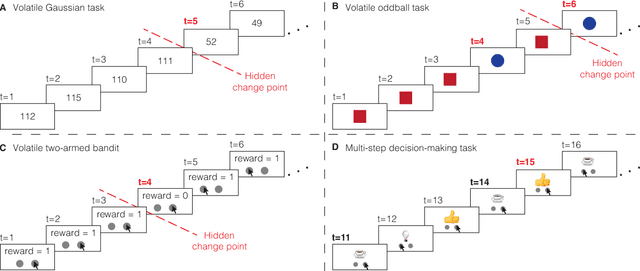
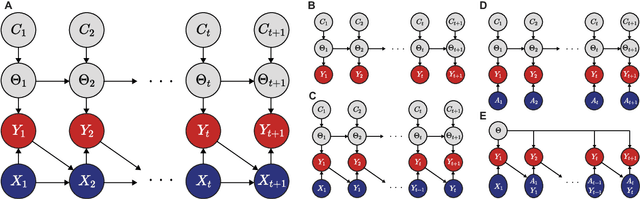
Surprising events trigger measurable brain activity and influence human behavior by affecting learning, memory, and decision-making. Currently there is, however, no consensus on the definition of surprise. Here we identify 18 mathematical definitions of surprise in a unifying framework. We first propose a technical classification of these definitions into three groups based on their dependence on an agent's belief, show how they relate to each other, and prove under what conditions they are indistinguishable. Going beyond this technical analysis, we propose a taxonomy of surprise definitions and classify them into four conceptual categories based on the quantity they measure: (i) 'prediction surprise' measures a mismatch between a prediction and an observation; (ii) 'change-point detection surprise' measures the probability of a change in the environment; (iii) 'confidence-corrected surprise' explicitly accounts for the effect of confidence; and (iv) 'information gain surprise' measures the belief-update upon a new observation. The taxonomy poses the foundation for principled studies of the functional roles and physiological signatures of surprise in the brain.

Kernel Memory Networks: A Unifying Framework for Memory Modeling

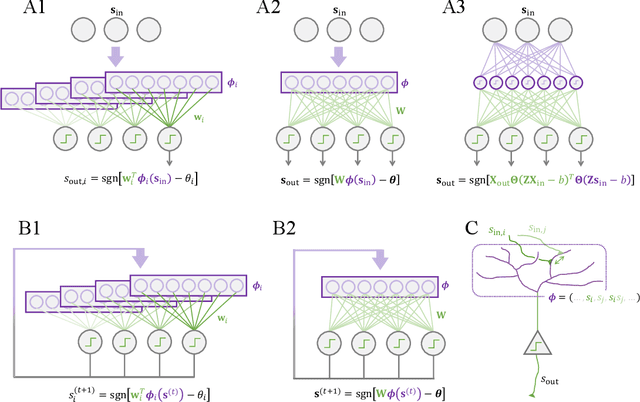
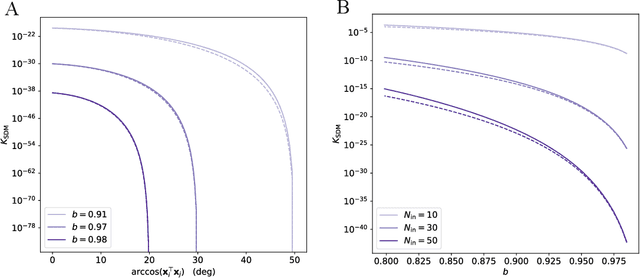
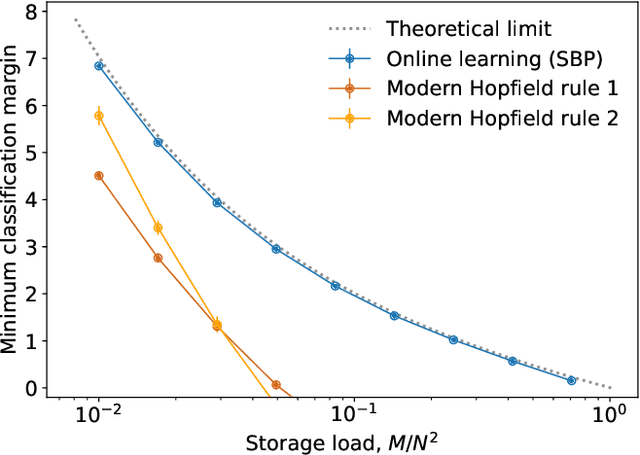
We consider the problem of training a neural network to store a set of patterns with maximal noise robustness. A solution, in terms of optimal weights and state update rules, is derived by training each individual neuron to perform either kernel classification or interpolation with a minimum weight norm. By applying this method to feed-forward and recurrent networks, we derive optimal networks that include, as special cases, many of the hetero- and auto-associative memory models that have been proposed over the past years, such as modern Hopfield networks and Kanerva's sparse distributed memory. We generalize Kanerva's model and demonstrate a simple way to design a kernel memory network that can store an exponential number of continuous-valued patterns with a finite basin of attraction. The framework of kernel memory networks offers a simple and intuitive way to understand the storage capacity of previous memory models, and allows for new biological interpretations in terms of dendritic non-linearities and synaptic clustering.

Neural NID Rules

Abstract object properties and their relations are deeply rooted in human common sense, allowing people to predict the dynamics of the world even in situations that are novel but governed by familiar laws of physics. Standard machine learning models in model-based reinforcement learning are inadequate to generalize in this way. Inspired by the classic framework of noisy indeterministic deictic (NID) rules, we introduce here Neural NID, a method that learns abstract object properties and relations between objects with a suitably regularized graph neural network. We validate the greater generalization capability of Neural NID on simple benchmarks specifically designed to assess the transition dynamics learned by the model.

Fitting summary statistics of neural data with a differentiable spiking network simulator

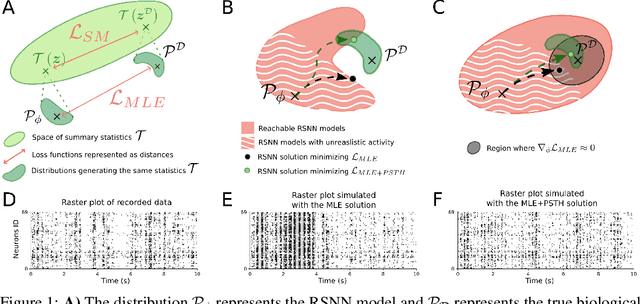
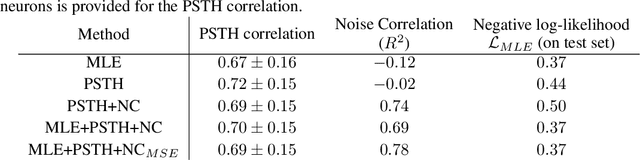
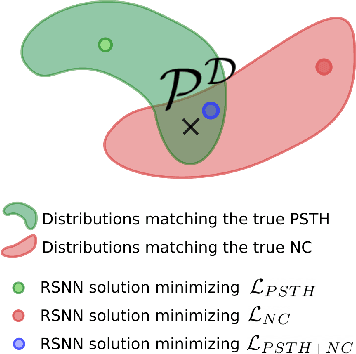
Fitting network models to neural activity is becoming an important tool in neuroscience. A popular approach is to model a brain area with a probabilistic recurrent spiking network whose parameters maximize the likelihood of the recorded activity. Although this is widely used, we show that the resulting model does not produce realistic neural activity and wrongly estimates the connectivity matrix when neurons that are not recorded have a substantial impact on the recorded network. To correct for this, we suggest to augment the log-likelihood with terms that measure the dissimilarity between simulated and recorded activity. This dissimilarity is defined via summary statistics commonly used in neuroscience, and the optimization is efficient because it relies on back-propagation through the stochastically simulated spike trains. We analyze this method theoretically and show empirically that it generates more realistic activity statistics and recovers the connectivity matrix better than other methods.

Geometry of the Loss Landscape in Overparameterized Neural Networks: Symmetries and Invariances

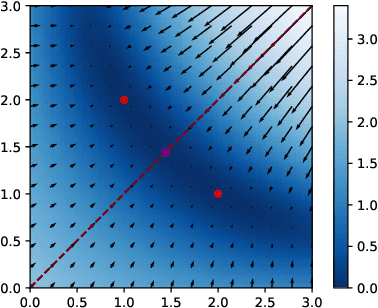
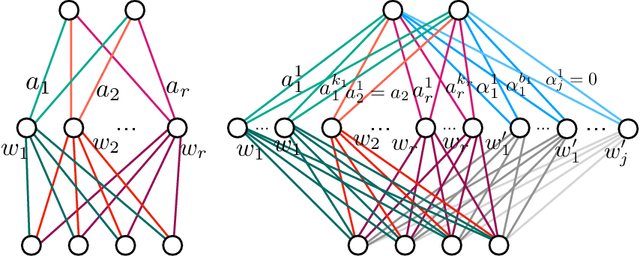
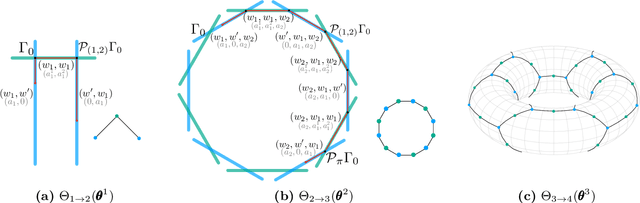
We study how permutation symmetries in overparameterized multi-layer neural networks generate `symmetry-induced' critical points. Assuming a network with $ L $ layers of minimal widths $ r_1^*, \ldots, r_{L-1}^* $ reaches a zero-loss minimum at $ r_1^*! \cdots r_{L-1}^*! $ isolated points that are permutations of one another, we show that adding one extra neuron to each layer is sufficient to connect all these previously discrete minima into a single manifold. For a two-layer overparameterized network of width $ r^*+ h =: m $ we explicitly describe the manifold of global minima: it consists of $ T(r^*, m) $ affine subspaces of dimension at least $ h $ that are connected to one another. For a network of width $m$, we identify the number $G(r,m)$ of affine subspaces containing only symmetry-induced critical points that are related to the critical points of a smaller network of width $r<r^*$. Via a combinatorial analysis, we derive closed-form formulas for $ T $ and $ G $ and show that the number of symmetry-induced critical subspaces dominates the number of affine subspaces forming the global minima manifold in the mildly overparameterized regime (small $ h $) and vice versa in the vastly overparameterized regime ($h \gg r^*$). Our results provide new insights into the minimization of the non-convex loss function of overparameterized neural networks.

An Approximate Bayesian Approach to Surprise-Based Learning

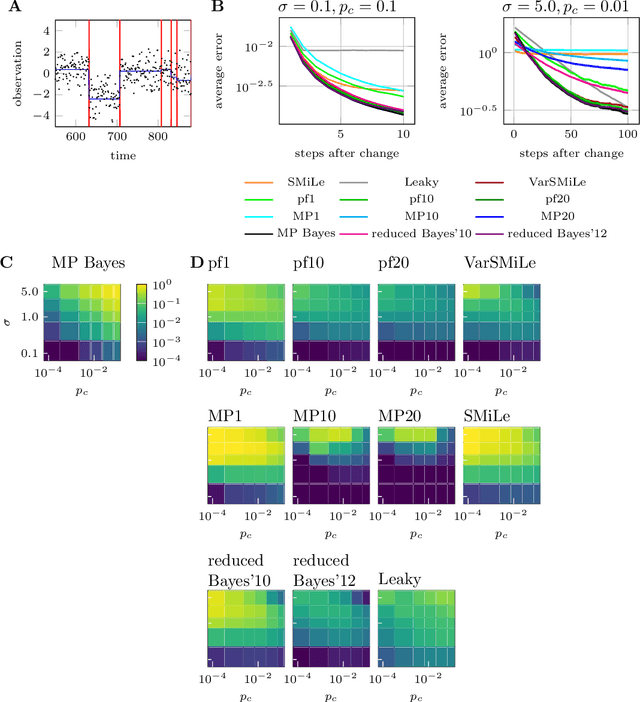
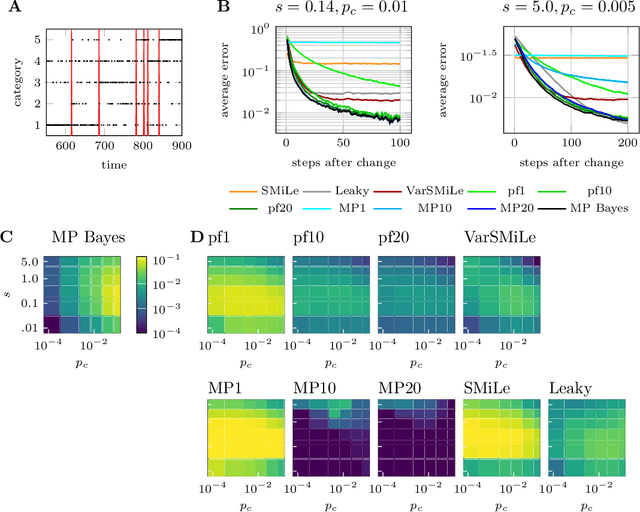
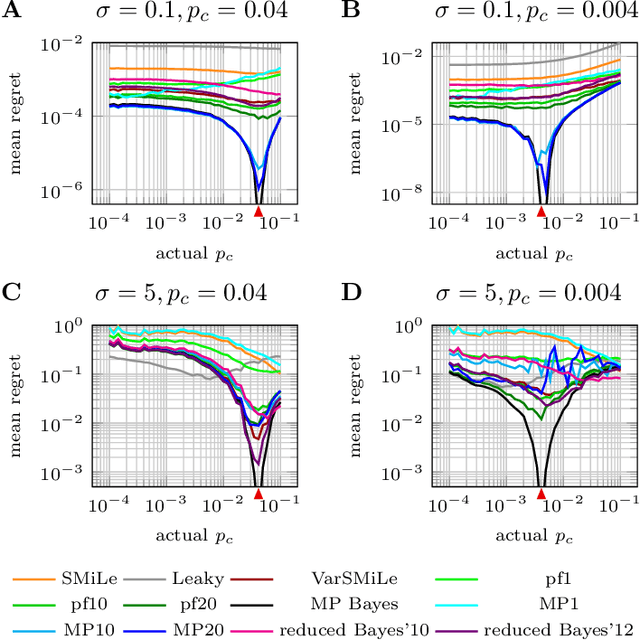
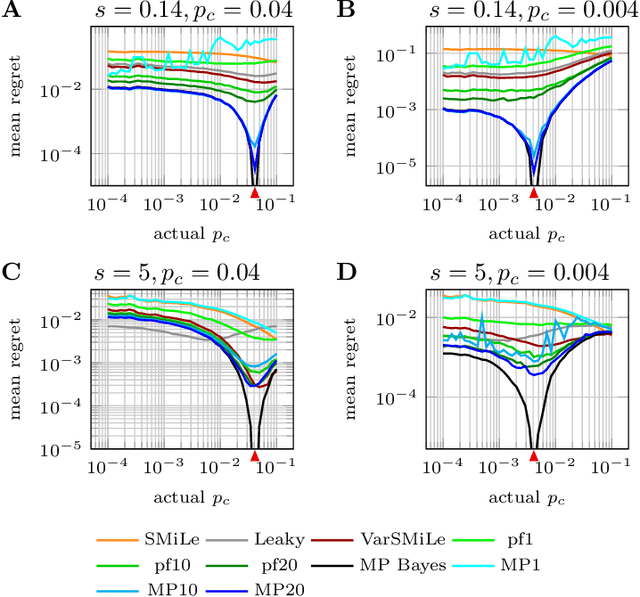
Surprise-based learning allows agents to adapt quickly in non-stationary stochastic environments. Most existing approaches to surprise-based learning and change point detection assume either implicitly or explicitly a simple, hierarchical generative model of observation sequences that are characterized by stationary periods separated by sudden changes. In this work we show that exact Bayesian inference gives naturally rise to a surprise-modulated trade-off between forgetting and integrating the new observations with the current belief. We demonstrate that many existing approximate Bayesian approaches also show surprise-based modulation of learning rates, and we derive novel particle filters and variational filters with update rules that exhibit surprise-based modulation. Our derived filters have a constant scaling in observation sequence length and particularly simple update dynamics for any distribution in the exponential family. Empirical results show that these filters estimate parameters better than alternative approximate approaches and reach comparative levels of performance to computationally more expensive algorithms. The theoretical insight of casting various approaches under the same interpretation of surprise-based learning, as well as the proposed filters, may find useful applications in reinforcement learning in non-stationary environments and in the analysis of animal and human behavior.

Weight-space symmetry in deep networks gives rise to permutation saddles, connected by equal-loss valleys across the loss landscape

The permutation symmetry of neurons in each layer of a deep neural network gives rise not only to multiple equivalent global minima of the loss function, but also to first-order saddle points located on the path between the global minima. In a network of $d-1$ hidden layers with $n_k$ neurons in layers $k = 1, \ldots, d$, we construct smooth paths between equivalent global minima that lead through a `permutation point' where the input and output weight vectors of two neurons in the same hidden layer $k$ collide and interchange. We show that such permutation points are critical points with at least $n_{k+1}$ vanishing eigenvalues of the Hessian matrix of second derivatives indicating a local plateau of the loss function. We find that a permutation point for the exchange of neurons $i$ and $j$ transits into a flat valley (or generally, an extended plateau of $n_{k+1}$ flat dimensions) that enables all $n_k!$ permutations of neurons in a given layer $k$ at the same loss value. Moreover, we introduce high-order permutation points by exploiting the recursive structure in neural network functions, and find that the number of $K^{\text{th}}$-order permutation points is at least by a factor $\sum_{k=1}^{d-1}\frac{1}{2!^K}{n_k-K \choose K}$ larger than the (already huge) number of equivalent global minima. In two tasks, we illustrate numerically that some of the permutation points correspond to first-order saddles (`permutation saddles'): first, in a toy network with a single hidden layer on a function approximation task and, second, in a multilayer network on the MNIST task. Our geometric approach yields a lower bound on the number of critical points generated by weight-space symmetries and provides a simple intuitive link between previous mathematical results and numerical observations.