Flat Channels to Infinity in Neural Loss Landscapes

The loss landscapes of neural networks contain minima and saddle points that may be connected in flat regions or appear in isolation. We identify and characterize a special structure in the loss landscape: channels along which the loss decreases extremely slowly, while the output weights of at least two neurons, $a_i$ and $a_j$, diverge to $\pm$infinity, and their input weight vectors, $\mathbf{w_i}$ and $\mathbf{w_j}$, become equal to each other. At convergence, the two neurons implement a gated linear unit: $a_i\sigma(\mathbf{w_i} \cdot \mathbf{x}) + a_j\sigma(\mathbf{w_j} \cdot \mathbf{x}) \rightarrow \sigma(\mathbf{w} \cdot \mathbf{x}) + (\mathbf{v} \cdot \mathbf{x}) \sigma'(\mathbf{w} \cdot \mathbf{x})$. Geometrically, these channels to infinity are asymptotically parallel to symmetry-induced lines of critical points. Gradient flow solvers, and related optimization methods like SGD or ADAM, reach the channels with high probability in diverse regression settings, but without careful inspection they look like flat local minima with finite parameter values. Our characterization provides a comprehensive picture of these quasi-flat regions in terms of gradient dynamics, geometry, and functional interpretation. The emergence of gated linear units at the end of the channels highlights a surprising aspect of the computational capabilities of fully connected layers.

Expand-and-Cluster: Exact Parameter Recovery of Neural Networks

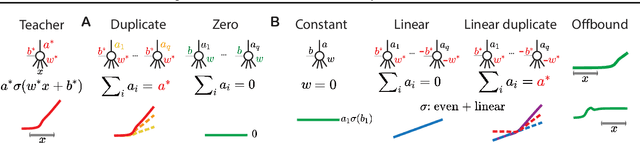
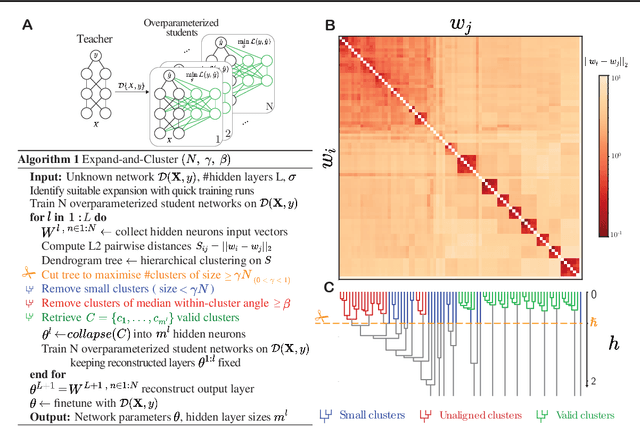
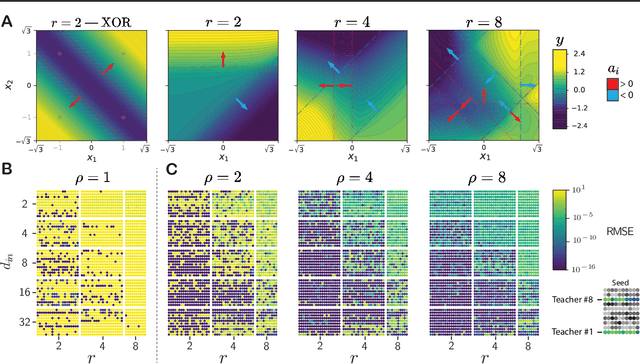
Can we recover the hidden parameters of an Artificial Neural Network (ANN) by probing its input-output mapping? We propose a systematic method, called `Expand-and-Cluster' that needs only the number of hidden layers and the activation function of the probed ANN to identify all network parameters. In the expansion phase, we train a series of student networks of increasing size using the probed data of the ANN as a teacher. Expansion stops when a minimal loss is consistently reached in student networks of a given size. In the clustering phase, weight vectors of the expanded students are clustered, which allows structured pruning of superfluous neurons in a principled way. We find that an overparameterization of a factor four is sufficient to reliably identify the minimal number of neurons and to retrieve the original network parameters in $80\%$ of tasks across a family of 150 toy problems of variable difficulty. Furthermore, a teacher network trained on MNIST data can be identified with less than $5\%$ overhead in the neuron number. Thus, while direct training of a student network with a size identical to that of the teacher is practically impossible because of the non-convex loss function, training with mild overparameterization followed by clustering and structured pruning correctly identifies the target network.

MLPGradientFlow: going with the flow of multilayer perceptrons (and finding minima fast and accurately)

MLPGradientFlow is a software package to solve numerically the gradient flow differential equation $\dot \theta = -\nabla \mathcal L(\theta; \mathcal D)$, where $\theta$ are the parameters of a multi-layer perceptron, $\mathcal D$ is some data set, and $\nabla \mathcal L$ is the gradient of a loss function. We show numerically that adaptive first- or higher-order integration methods based on Runge-Kutta schemes have better accuracy and convergence speed than gradient descent with the Adam optimizer. However, we find Newton's method and approximations like BFGS preferable to find fixed points (local and global minima of $\mathcal L$) efficiently and accurately. For small networks and data sets, gradients are usually computed faster than in pytorch and Hessian are computed at least $5\times$ faster. Additionally, the package features an integrator for a teacher-student setup with bias-free, two-layer networks trained with standard Gaussian input in the limit of infinite data. The code is accessible at https://github.com/jbrea/MLPGradientFlow.jl.

Spiking neural networks trained with backpropagation for low power neuromorphic implementation of voice activity detection

Recent advances in Voice Activity Detection (VAD) are driven by artificial and Recurrent Neural Networks (RNNs), however, using a VAD system in battery-operated devices requires further power efficiency. This can be achieved by neuromorphic hardware, which enables Spiking Neural Networks (SNNs) to perform inference at very low energy consumption. Spiking networks are characterized by their ability to process information efficiently, in a sparse cascade of binary events in time called spikes. However, a big performance gap separates artificial from spiking networks, mostly due to a lack of powerful SNN training algorithms. To overcome this problem we exploit an SNN model that can be recast into an RNN-like model and trained with known deep learning techniques. We describe an SNN training procedure that achieves low spiking activity and pruning algorithms to remove 85% of the network connections with no performance loss. The model achieves state-of-the-art performance with a fraction of power consumption comparing to other methods.