Learning Gaussian Multi-Index Models with Gradient Flow: Time Complexity and Directional Convergence

This work focuses on the gradient flow dynamics of a neural network model that uses correlation loss to approximate a multi-index function on high-dimensional standard Gaussian data. Specifically, the multi-index function we consider is a sum of neurons $f^*(x) \!=\! \sum_{j=1}^k \! \sigma^*(v_j^T x)$ where $v_1, \dots, v_k$ are unit vectors, and $\sigma^*$ lacks the first and second Hermite polynomials in its Hermite expansion. It is known that, for the single-index case ($k\!=\!1$), overcoming the search phase requires polynomial time complexity. We first generalize this result to multi-index functions characterized by vectors in arbitrary directions. After the search phase, it is not clear whether the network neurons converge to the index vectors, or get stuck at a sub-optimal solution. When the index vectors are orthogonal, we give a complete characterization of the fixed points and prove that neurons converge to the nearest index vectors. Therefore, using $n \! \asymp \! k \log k$ neurons ensures finding the full set of index vectors with gradient flow with high probability over random initialization. When $ v_i^T v_j \!=\! \beta \! \geq \! 0$ for all $i \neq j$, we prove the existence of a sharp threshold $\beta_c \!=\! c/(c+k)$ at which the fixed point that computes the average of the index vectors transitions from a saddle point to a minimum. Numerical simulations show that using a correlation loss and a mild overparameterization suffices to learn all of the index vectors when they are nearly orthogonal, however, the correlation loss fails when the dot product between the index vectors exceeds a certain threshold.

Learning Associative Memories with Gradient Descent

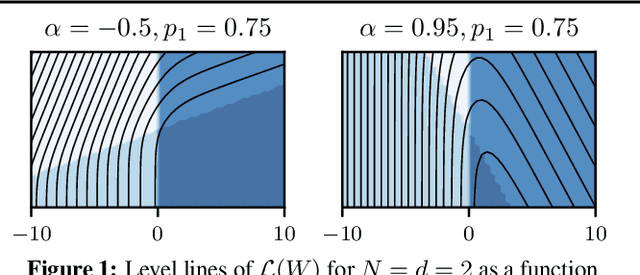
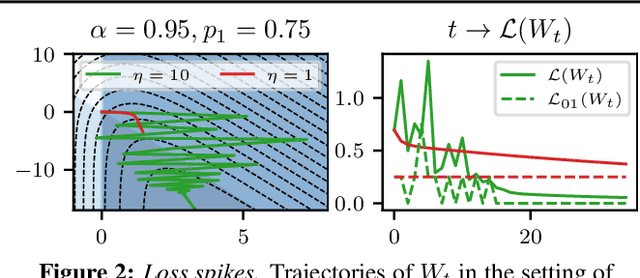
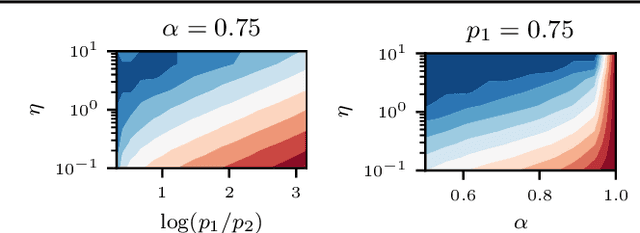
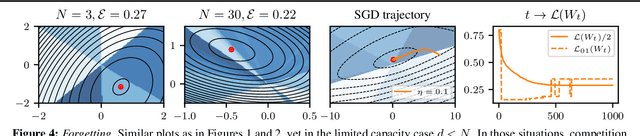
This work focuses on the training dynamics of one associative memory module storing outer products of token embeddings. We reduce this problem to the study of a system of particles, which interact according to properties of the data distribution and correlations between embeddings. Through theory and experiments, we provide several insights. In overparameterized regimes, we obtain logarithmic growth of the ``classification margins.'' Yet, we show that imbalance in token frequencies and memory interferences due to correlated embeddings lead to oscillatory transitory regimes. The oscillations are more pronounced with large step sizes, which can create benign loss spikes, although these learning rates speed up the dynamics and accelerate the asymptotic convergence. In underparameterized regimes, we illustrate how the cross-entropy loss can lead to suboptimal memorization schemes. Finally, we assess the validity of our findings on small Transformer models.

The Loss Landscape of Shallow ReLU-like Neural Networks: Stationary Points, Saddle Escaping, and Network Embedding

In this paper, we investigate the loss landscape of one-hidden-layer neural networks with ReLU-like activation functions trained with the empirical squared loss. As the activation function is non-differentiable, it is so far unclear how to completely characterize the stationary points. We propose the conditions for stationarity that apply to both non-differentiable and differentiable cases. Additionally, we show that, if a stationary point does not contain "escape neurons", which are defined with first-order conditions, then it must be a local minimum. Moreover, for the scalar-output case, the presence of an escape neuron guarantees that the stationary point is not a local minimum. Our results refine the description of the saddle-to-saddle training process starting from infinitesimally small (vanishing) initialization for shallow ReLU-like networks, linking saddle escaping directly with the parameter changes of escape neurons. Moreover, we are also able to fully discuss how network embedding, which is to instantiate a narrower network within a wider network, reshapes the stationary points.

Expand-and-Cluster: Exact Parameter Recovery of Neural Networks

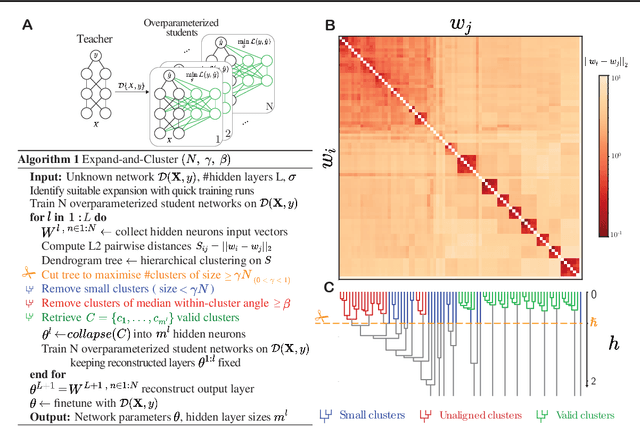
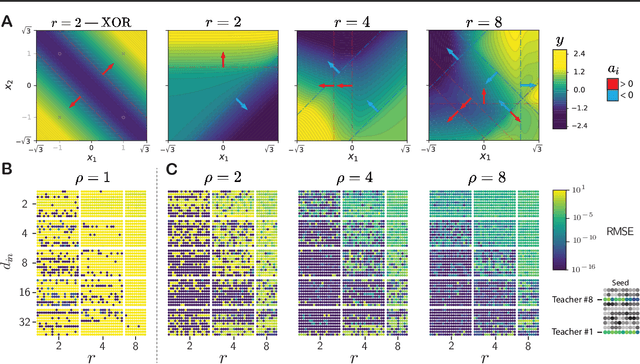
Can we recover the hidden parameters of an Artificial Neural Network (ANN) by probing its input-output mapping? We propose a systematic method, called `Expand-and-Cluster' that needs only the number of hidden layers and the activation function of the probed ANN to identify all network parameters. In the expansion phase, we train a series of student networks of increasing size using the probed data of the ANN as a teacher. Expansion stops when a minimal loss is consistently reached in student networks of a given size. In the clustering phase, weight vectors of the expanded students are clustered, which allows structured pruning of superfluous neurons in a principled way. We find that an overparameterization of a factor four is sufficient to reliably identify the minimal number of neurons and to retrieve the original network parameters in $80\%$ of tasks across a family of 150 toy problems of variable difficulty. Furthermore, a teacher network trained on MNIST data can be identified with less than $5\%$ overhead in the neuron number. Thus, while direct training of a student network with a size identical to that of the teacher is practically impossible because of the non-convex loss function, training with mild overparameterization followed by clustering and structured pruning correctly identifies the target network.

Understanding out-of-distribution accuracies through quantifying difficulty of test samples

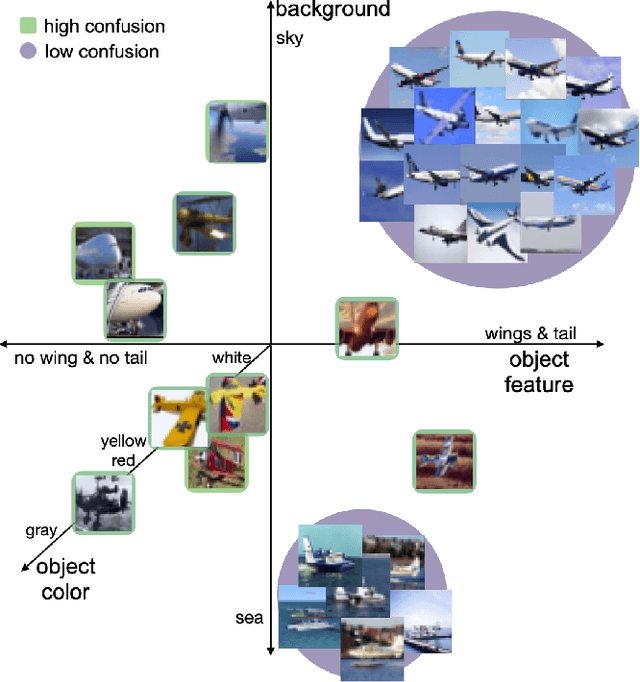
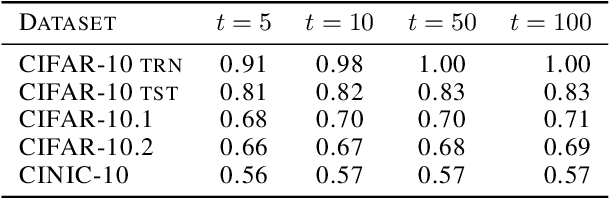
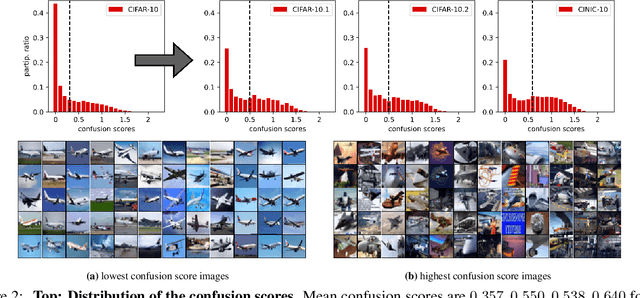
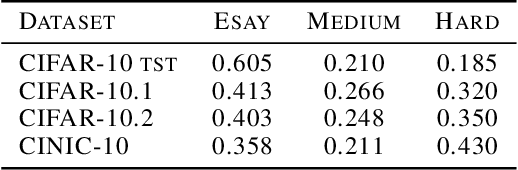
Existing works show that although modern neural networks achieve remarkable generalization performance on the in-distribution (ID) dataset, the accuracy drops significantly on the out-of-distribution (OOD) datasets \cite{recht2018cifar, recht2019imagenet}. To understand why a variety of models consistently make more mistakes in the OOD datasets, we propose a new metric to quantify the difficulty of the test images (either ID or OOD) that depends on the interaction of the training dataset and the model. In particular, we introduce \textit{confusion score} as a label-free measure of image difficulty which quantifies the amount of disagreement on a given test image based on the class conditional probabilities estimated by an ensemble of trained models. Using the confusion score, we investigate CIFAR-10 and its OOD derivatives. Next, by partitioning test and OOD datasets via their confusion scores, we predict the relationship between ID and OOD accuracies for various architectures. This allows us to obtain an estimator of the OOD accuracy of a given model only using ID test labels. Our observations indicate that the biggest contribution to the accuracy drop comes from images with high confusion scores. Upon further inspection, we report on the nature of the misclassified images grouped by their confusion scores: \textit{(i)} images with high confusion scores contain \textit{weak spurious correlations} that appear in multiple classes in the training data and lack clear \textit{class-specific features}, and \textit{(ii)} images with low confusion scores exhibit spurious correlations that belong to another class, namely \textit{class-specific spurious correlations}.

Weight-space symmetry in deep networks gives rise to permutation saddles, connected by equal-loss valleys across the loss landscape

The permutation symmetry of neurons in each layer of a deep neural network gives rise not only to multiple equivalent global minima of the loss function, but also to first-order saddle points located on the path between the global minima. In a network of $d-1$ hidden layers with $n_k$ neurons in layers $k = 1, \ldots, d$, we construct smooth paths between equivalent global minima that lead through a `permutation point' where the input and output weight vectors of two neurons in the same hidden layer $k$ collide and interchange. We show that such permutation points are critical points with at least $n_{k+1}$ vanishing eigenvalues of the Hessian matrix of second derivatives indicating a local plateau of the loss function. We find that a permutation point for the exchange of neurons $i$ and $j$ transits into a flat valley (or generally, an extended plateau of $n_{k+1}$ flat dimensions) that enables all $n_k!$ permutations of neurons in a given layer $k$ at the same loss value. Moreover, we introduce high-order permutation points by exploiting the recursive structure in neural network functions, and find that the number of $K^{\text{th}}$-order permutation points is at least by a factor $\sum_{k=1}^{d-1}\frac{1}{2!^K}{n_k-K \choose K}$ larger than the (already huge) number of equivalent global minima. In two tasks, we illustrate numerically that some of the permutation points correspond to first-order saddles (`permutation saddles'): first, in a toy network with a single hidden layer on a function approximation task and, second, in a multilayer network on the MNIST task. Our geometric approach yields a lower bound on the number of critical points generated by weight-space symmetries and provides a simple intuitive link between previous mathematical results and numerical observations.