Matryoshka Policy Gradient for Entropy-Regularized RL: Convergence and Global Optimality

A novel Policy Gradient (PG) algorithm, called Matryoshka Policy Gradient (MPG), is introduced and studied, in the context of max-entropy reinforcement learning, where an agent aims at maximising entropy bonuses additional to its cumulative rewards. MPG differs from standard PG in that it trains a sequence of policies to learn finite horizon tasks simultaneously, instead of a single policy for the single standard objective. For softmax policies, we prove convergence of MPG and global optimality of the limit by showing that the only critical point of the MPG objective is the optimal policy; these results hold true even in the case of continuous compact state space. MPG is intuitive, theoretically sound and we furthermore show that the optimal policy of the standard max-entropy objective can be approximated arbitrarily well by the optimal policy of the MPG framework. Finally, we justify that MPG is well suited when the policies are parametrized with neural networks and we provide an simple criterion to verify the global optimality of the policy at convergence. As a proof of concept, we evaluate numerically MPG on standard test benchmarks.

Deep Linear Networks Dynamics: Low-Rank Biases Induced by Initialization Scale and L2 Regularization

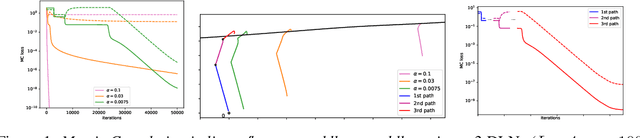
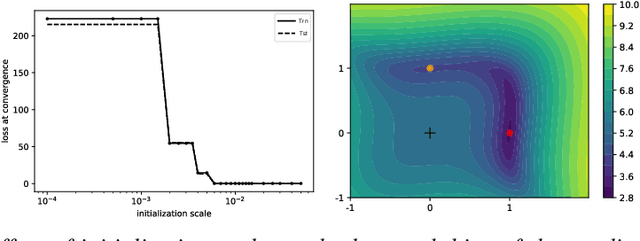
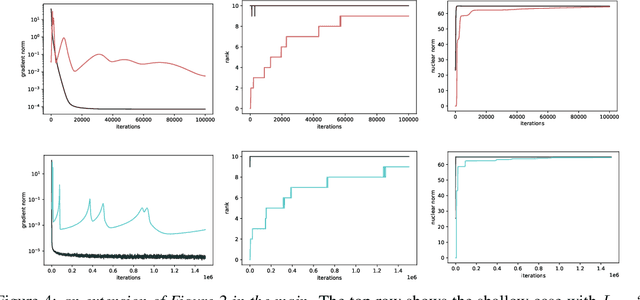
For deep linear networks (DLN), various hyperparameters alter the dynamics of training dramatically. We investigate how the rank of the linear map found by gradient descent is affected by (1) the initialization norm and (2) the addition of $L_{2}$ regularization on the parameters. For (1), we study two regimes: (1a) the linear/lazy regime, for large norm initialization; (1b) a \textquotedbl saddle-to-saddle\textquotedbl{} regime for small initialization norm. In the (1a) setting, the dynamics of a DLN of any depth is similar to that of a standard linear model, without any low-rank bias. In the (1b) setting, we conjecture that throughout training, gradient descent approaches a sequence of saddles, each corresponding to linear maps of increasing rank, until reaching a minimal rank global minimum. We support this conjecture with a partial proof and some numerical experiments. For (2), we show that adding a $L_{2}$ regularization on the parameters corresponds to the addition to the cost of a $L_{p}$-Schatten (quasi)norm on the linear map with $p=\frac{2}{L}$ (for a depth-$L$ network), leading to a stronger low-rank bias as $L$ grows. The effect of $L_{2}$ regularization on the loss surface depends on the depth: for shallow networks, all critical points are either strict saddles or global minima, whereas for deep networks, some local minima appear. We numerically observe that these local minima can generalize better than global ones in some settings.

Geometry of the Loss Landscape in Overparameterized Neural Networks: Symmetries and Invariances

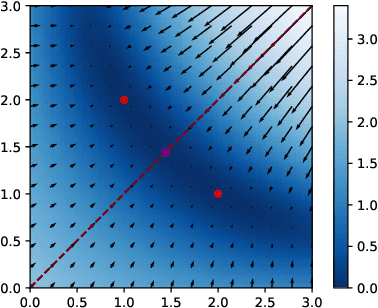
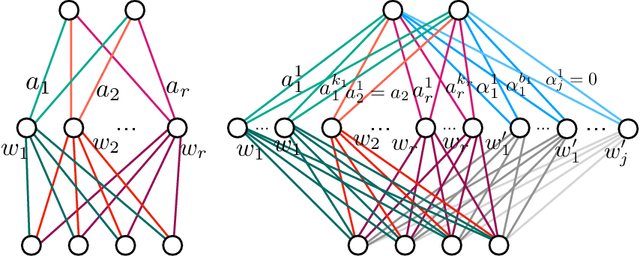
We study how permutation symmetries in overparameterized multi-layer neural networks generate `symmetry-induced' critical points. Assuming a network with $ L $ layers of minimal widths $ r_1^*, \ldots, r_{L-1}^* $ reaches a zero-loss minimum at $ r_1^*! \cdots r_{L-1}^*! $ isolated points that are permutations of one another, we show that adding one extra neuron to each layer is sufficient to connect all these previously discrete minima into a single manifold. For a two-layer overparameterized network of width $ r^*+ h =: m $ we explicitly describe the manifold of global minima: it consists of $ T(r^*, m) $ affine subspaces of dimension at least $ h $ that are connected to one another. For a network of width $m$, we identify the number $G(r,m)$ of affine subspaces containing only symmetry-induced critical points that are related to the critical points of a smaller network of width $r<r^*$. Via a combinatorial analysis, we derive closed-form formulas for $ T $ and $ G $ and show that the number of symmetry-induced critical subspaces dominates the number of affine subspaces forming the global minima manifold in the mildly overparameterized regime (small $ h $) and vice versa in the vastly overparameterized regime ($h \gg r^*$). Our results provide new insights into the minimization of the non-convex loss function of overparameterized neural networks.