Origami in N dimensions: How feed-forward networks manufacture linear separability
Paper and Code
Mar 21, 2022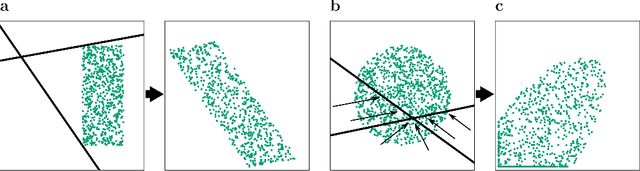
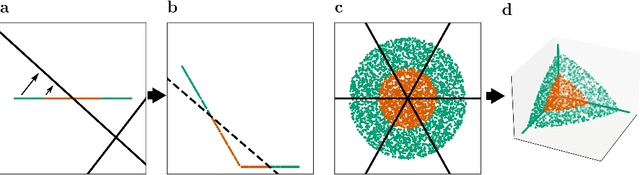
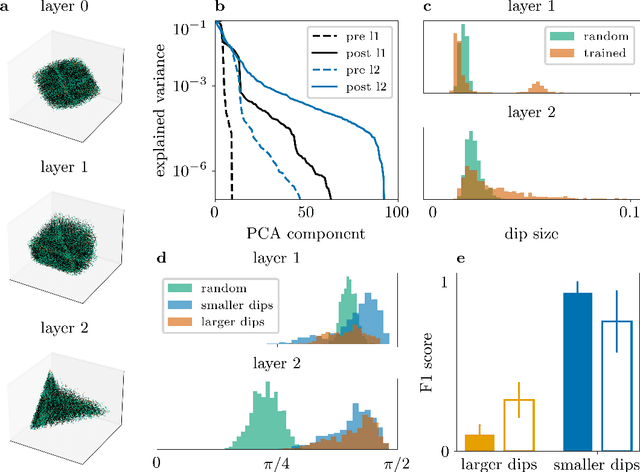
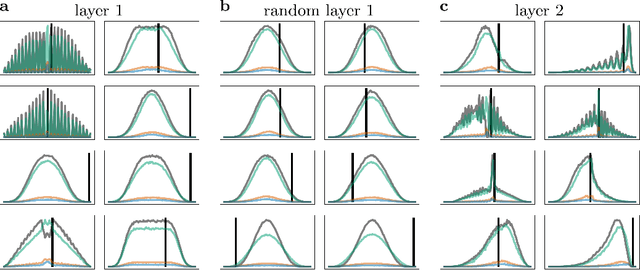
Neural networks can implement arbitrary functions. But, mechanistically, what are the tools at their disposal to construct the target? For classification tasks, the network must transform the data classes into a linearly separable representation in the final hidden layer. We show that a feed-forward architecture has one primary tool at hand to achieve this separability: progressive folding of the data manifold in unoccupied higher dimensions. The operation of folding provides a useful intuition in low-dimensions that generalizes to high ones. We argue that an alternative method based on shear, requiring very deep architectures, plays only a small role in real-world networks. The folding operation, however, is powerful as long as layers are wider than the data dimensionality, allowing efficient solutions by providing access to arbitrary regions in the distribution, such as data points of one class forming islands within the other classes. We argue that a link exists between the universal approximation property in ReLU networks and the fold-and-cut theorem (Demaine et al., 1998) dealing with physical paper folding. Based on the mechanistic insight, we predict that the progressive generation of separability is necessarily accompanied by neurons showing mixed selectivity and bimodal tuning curves. This is validated in a network trained on the poker hand task, showing the emergence of bimodal tuning curves during training. We hope that our intuitive picture of the data transformation in deep networks can help to provide interpretability, and discuss possible applications to the theory of convolutional networks, loss landscapes, and generalization. TL;DR: Shows that the internal processing of deep networks can be thought of as literal folding operations on the data distribution in the N-dimensional activation space. A link to a well-known theorem in origami theory is provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge