Connectivity structure and dynamics of nonlinear recurrent neural networks

We develop a theory to analyze how structure in connectivity shapes the high-dimensional, internally generated activity of nonlinear recurrent neural networks. Using two complementary methods -- a path-integral calculation of fluctuations around the saddle point, and a recently introduced two-site cavity approach -- we derive analytic expressions that characterize important features of collective activity, including its dimensionality and temporal correlations. To model structure in the coupling matrices of real neural circuits, such as synaptic connectomes obtained through electron microscopy, we introduce the random-mode model, which parameterizes a coupling matrix using random input and output modes and a specified spectrum. This model enables systematic study of the effects of low-dimensional structure in connectivity on neural activity. These effects manifest in features of collective activity, that we calculate, and can be undetectable when analyzing only single-neuron activities. We derive a relation between the effective rank of the coupling matrix and the dimension of activity. By extending the random-mode model, we compare the effects of single-neuron heterogeneity and low-dimensional connectivity. We also investigate the impact of structured overlaps between input and output modes, a feature of biological coupling matrices. Our theory provides tools to relate neural-network architecture and collective dynamics in artificial and biological systems.

Coding schemes in neural networks learning classification tasks

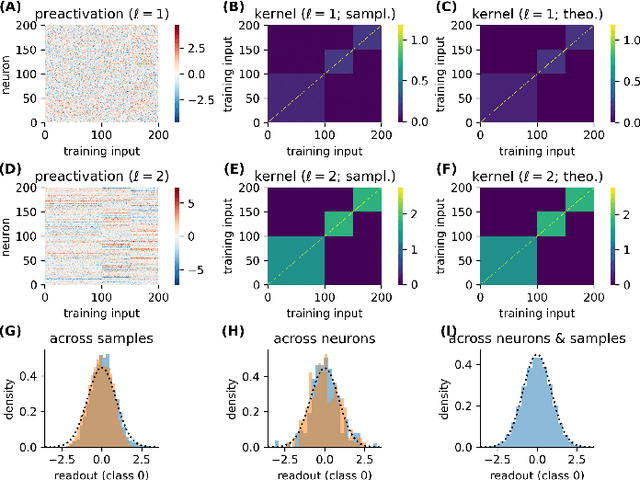
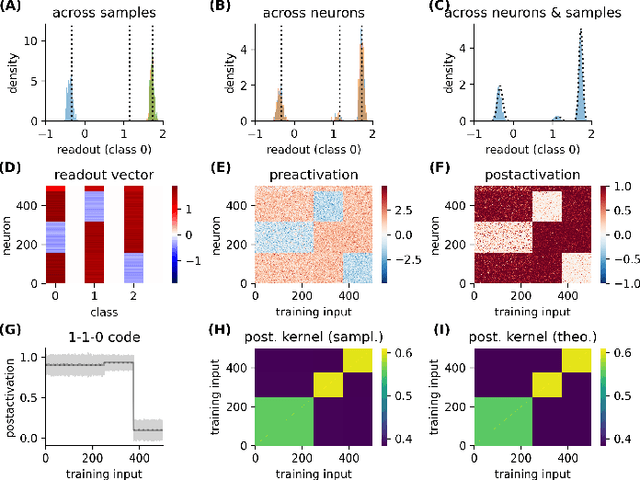
Neural networks posses the crucial ability to generate meaningful representations of task-dependent features. Indeed, with appropriate scaling, supervised learning in neural networks can result in strong, task-dependent feature learning. However, the nature of the emergent representations, which we call the `coding scheme', is still unclear. To understand the emergent coding scheme, we investigate fully-connected, wide neural networks learning classification tasks using the Bayesian framework where learning shapes the posterior distribution of the network weights. Consistent with previous findings, our analysis of the feature learning regime (also known as `non-lazy', `rich', or `mean-field' regime) shows that the networks acquire strong, data-dependent features. Surprisingly, the nature of the internal representations depends crucially on the neuronal nonlinearity. In linear networks, an analog coding scheme of the task emerges. Despite the strong representations, the mean predictor is identical to the lazy case. In nonlinear networks, spontaneous symmetry breaking leads to either redundant or sparse coding schemes. Our findings highlight how network properties such as scaling of weights and neuronal nonlinearity can profoundly influence the emergent representations.

Unified Field Theory for Deep and Recurrent Neural Networks

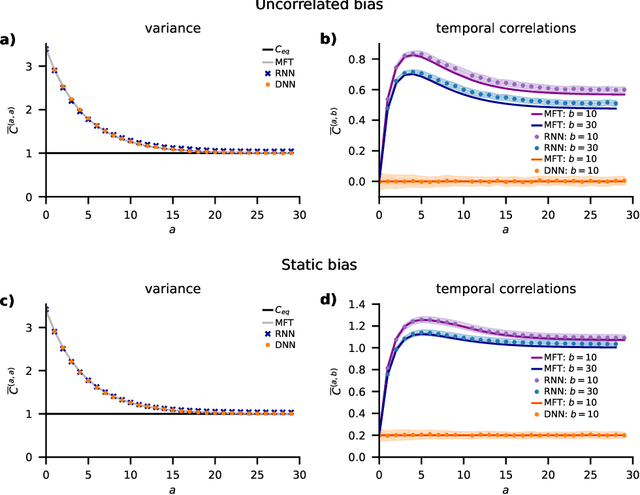
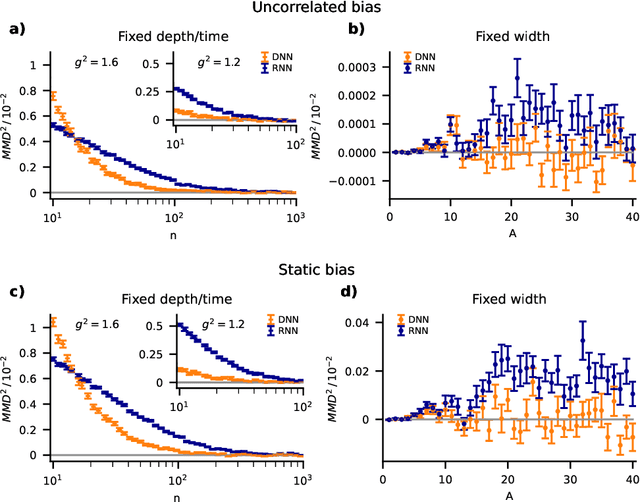
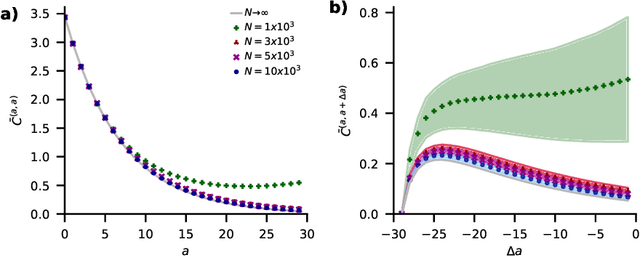
Understanding capabilities and limitations of different network architectures is of fundamental importance to machine learning. Bayesian inference on Gaussian processes has proven to be a viable approach for studying recurrent and deep networks in the limit of infinite layer width, $n\to\infty$. Here we present a unified and systematic derivation of the mean-field theory for both architectures that starts from first principles by employing established methods from statistical physics of disordered systems. The theory elucidates that while the mean-field equations are different with regard to their temporal structure, they yet yield identical Gaussian kernels when readouts are taken at a single time point or layer, respectively. Bayesian inference applied to classification then predicts identical performance and capabilities for the two architectures. Numerically, we find that convergence towards the mean-field theory is typically slower for recurrent networks than for deep networks and the convergence speed depends non-trivially on the parameters of the weight prior as well as the depth or number of time steps, respectively. Our method exposes that Gaussian processes are but the lowest order of a systematic expansion in $1/n$. The formalism thus paves the way to investigate the fundamental differences between recurrent and deep architectures at finite widths $n$.