David G. Clark
Simplified derivations for high-dimensional convex learning problems
Dec 02, 2024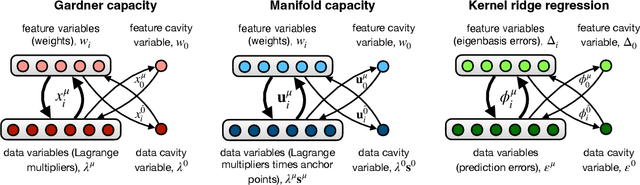
Abstract:Statistical physics provides tools for analyzing high-dimensional problems in machine learning and theoretical neuroscience. These calculations, particularly those using the replica method, often involve lengthy derivations that can obscure physical interpretation. We give concise, non-replica derivations of several key results and highlight their underlying similarities. Specifically, we introduce a cavity approach to analyzing high-dimensional learning problems and apply it to three cases: perceptron classification of points, perceptron classification of manifolds, and kernel ridge regression. These problems share a common structure -- a bipartite system of interacting feature and datum variables -- enabling a unified analysis. For perceptron-capacity problems, we identify a symmetry that allows derivation of correct capacities through a na\"ive method. These results match those obtained through the replica method.
Connectivity structure and dynamics of nonlinear recurrent neural networks
Sep 03, 2024



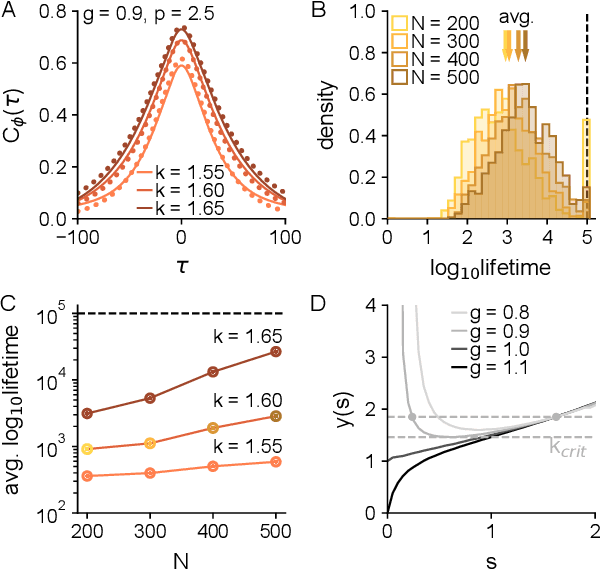
Abstract:We develop a theory to analyze how structure in connectivity shapes the high-dimensional, internally generated activity of nonlinear recurrent neural networks. Using two complementary methods -- a path-integral calculation of fluctuations around the saddle point, and a recently introduced two-site cavity approach -- we derive analytic expressions that characterize important features of collective activity, including its dimensionality and temporal correlations. To model structure in the coupling matrices of real neural circuits, such as synaptic connectomes obtained through electron microscopy, we introduce the random-mode model, which parameterizes a coupling matrix using random input and output modes and a specified spectrum. This model enables systematic study of the effects of low-dimensional structure in connectivity on neural activity. These effects manifest in features of collective activity, that we calculate, and can be undetectable when analyzing only single-neuron activities. We derive a relation between the effective rank of the coupling matrix and the dimension of activity. By extending the random-mode model, we compare the effects of single-neuron heterogeneity and low-dimensional connectivity. We also investigate the impact of structured overlaps between input and output modes, a feature of biological coupling matrices. Our theory provides tools to relate neural-network architecture and collective dynamics in artificial and biological systems.
Structure of activity in multiregion recurrent neural networks
Feb 20, 2024Abstract:Neural circuits are composed of multiple regions, each with rich dynamics and engaging in communication with other regions. The combination of local, within-region dynamics and global, network-level dynamics is thought to provide computational flexibility. However, the nature of such multiregion dynamics and the underlying synaptic connectivity patterns remain poorly understood. Here, we study the dynamics of recurrent neural networks with multiple interconnected regions. Within each region, neurons have a combination of random and structured recurrent connections. Motivated by experimental evidence of communication subspaces between cortical areas, these networks have low-rank connectivity between regions, enabling selective routing of activity. These networks exhibit two interacting forms of dynamics: high-dimensional fluctuations within regions and low-dimensional signal transmission between regions. To characterize this interaction, we develop a dynamical mean-field theory to analyze such networks in the limit where each region contains infinitely many neurons, with cross-region currents as key order parameters. Regions can act as both generators and transmitters of activity, roles that we show are in conflict. Specifically, taming the complexity of activity within a region is necessary for it to route signals to and from other regions. Unlike previous models of routing in neural circuits, which suppressed the activities of neuronal groups to control signal flow, routing in our model is achieved by exciting different high-dimensional activity patterns through a combination of connectivity structure and nonlinear recurrent dynamics. This theory provides insight into the interpretation of both multiregion neural data and trained neural networks.
Theory of coupled neuronal-synaptic dynamics
Feb 17, 2023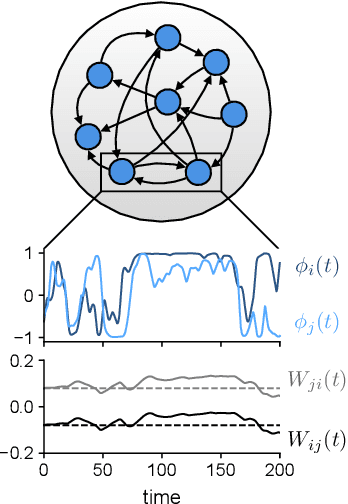
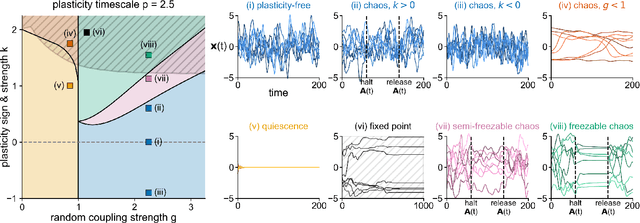
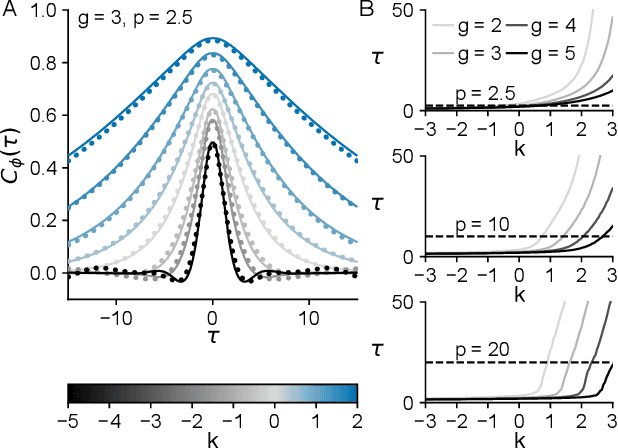
Abstract:In neural circuits, synapses influence neurons by shaping network dynamics, and neurons influence synapses through activity-dependent plasticity. Motivated by this fact, we study a network model in which neurons and synapses are mutually coupled dynamic variables. Model neurons obey dynamics shaped by synaptic couplings that fluctuate, in turn, about quenched random strengths in response to pre- and postsynaptic neuronal activity. Using dynamical mean-field theory, we compute the phase diagram of the combined neuronal-synaptic system, revealing several novel phases suggestive of computational function. In the regime in which the non-plastic system is chaotic, Hebbian plasticity slows chaos, while anti-Hebbian plasticity quickens chaos and generates an oscillatory component in neuronal activity. Deriving the spectrum of the joint neuronal-synaptic Jacobian reveals that these behaviors manifest as differential effects of eigenvalue repulsion. In the regime in which the non-plastic system is quiescent, Hebbian plasticity can induce chaos. In both regimes, sufficiently strong Hebbian plasticity creates exponentially many stable neuronal-synaptic fixed points that coexist with chaotic states. Finally, in chaotic states with sufficiently strong Hebbian plasticity, halting synaptic dynamics leaves a stable fixed point of neuronal dynamics, freezing the neuronal state. This phase of freezable chaos provides a novel mechanism of synaptic working memory in which a stable fixed point of neuronal dynamics is continuously destabilized through synaptic dynamics, allowing any neuronal state to be stored as a stable fixed point by halting synaptic plasticity.
Dimension of Activity in Random Neural Networks
Aug 07, 2022



Abstract:Neural networks are high-dimensional nonlinear dynamical systems that process information through the coordinated activity of many interconnected units. Understanding how biological and machine-learning networks function and learn requires knowledge of the structure of this coordinated activity, information contained in cross-covariances between units. Although dynamical mean field theory (DMFT) has elucidated several features of random neural networks -- in particular, that they can generate chaotic activity -- existing DMFT approaches do not support the calculation of cross-covariances. We solve this longstanding problem by extending the DMFT approach via a two-site cavity method. This reveals, for the first time, several spatial and temporal features of activity coordination, including the effective dimension, defined as the participation ratio of the spectrum of the covariance matrix. Our results provide a general analytical framework for studying the structure of collective activity in random neural networks and, more broadly, in high-dimensional nonlinear dynamical systems with quenched disorder.
Credit Assignment Through Broadcasting a Global Error Vector
Jun 08, 2021



Abstract:Backpropagation (BP) uses detailed, unit-specific feedback to train deep neural networks (DNNs) with remarkable success. That biological neural circuits appear to perform credit assignment, but cannot implement BP, implies the existence of other powerful learning algorithms. Here, we explore the extent to which a globally broadcast learning signal, coupled with local weight updates, enables training of DNNs. We present both a learning rule, called global error-vector broadcasting (GEVB), and a class of DNNs, called vectorized nonnegative networks (VNNs), in which this learning rule operates. VNNs have vector-valued units and nonnegative weights past the first layer. The GEVB learning rule generalizes three-factor Hebbian learning, updating each weight by an amount proportional to the inner product of the presynaptic activation and a globally broadcast error vector when the postsynaptic unit is active. We prove that these weight updates are matched in sign to the gradient, enabling accurate credit assignment. Moreover, at initialization, these updates are exactly proportional to the gradient in the limit of infinite network width. GEVB matches the performance of BP in VNNs, and in some cases outperforms direct feedback alignment (DFA) applied in conventional networks. Unlike DFA, GEVB successfully trains convolutional layers. Altogether, our theoretical and empirical results point to a surprisingly powerful role for a global learning signal in training DNNs.
Unsupervised Discovery of Temporal Structure in Noisy Data with Dynamical Components Analysis
May 23, 2019



Abstract:Linear dimensionality reduction methods are commonly used to extract low-dimensional structure from high-dimensional data. However, popular methods disregard temporal structure, rendering them prone to extracting noise rather than meaningful dynamics when applied to time series data. At the same time, many successful unsupervised learning methods for temporal, sequential and spatial data extract features which are predictive of their surrounding context. Combining these approaches, we introduce Dynamical Components Analysis (DCA), a linear dimensionality reduction method which discovers a subspace of high-dimensional time series data with maximal predictive information, defined as the mutual information between the past and future. We test DCA on synthetic examples and demonstrate its superior ability to extract dynamical structure compared to commonly used linear methods. We also apply DCA to several real-world datasets, showing that the dimensions extracted by DCA are more useful than those extracted by other methods for predicting future states and decoding auxiliary variables. Overall, DCA robustly extracts dynamical structure in noisy, high-dimensional data while retaining the computational efficiency and geometric interpretability of linear dimensionality reduction methods.
Spiking Linear Dynamical Systems on Neuromorphic Hardware for Low-Power Brain-Machine Interfaces
Jun 05, 2018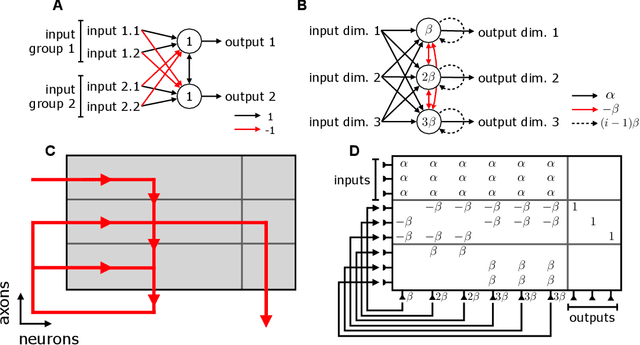
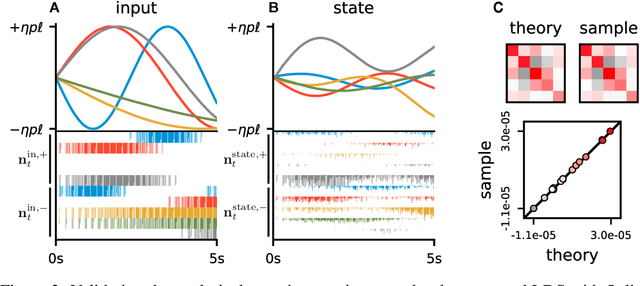
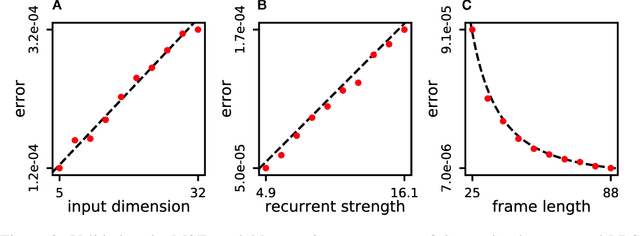
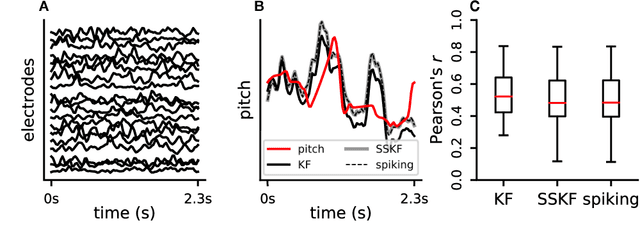
Abstract:Neuromorphic architectures achieve low-power operation by using many simple spiking neurons in lieu of traditional hardware. Here, we develop methods for precise linear computations in spiking neural networks and use these methods to map the evolution of a linear dynamical system (LDS) onto an existing neuromorphic chip: IBM's TrueNorth. We analytically characterize, and numerically validate, the discrepancy between the spiking LDS state sequence and that of its non-spiking counterpart. These analytical results shed light on the multiway tradeoff between time, space, energy, and accuracy in neuromorphic computation. To demonstrate the utility of our work, we implemented a neuromorphic Kalman filter (KF) and used it for offline decoding of human vocal pitch from neural data. The neuromorphic KF could be used for low-power filtering in domains beyond neuroscience, such as navigation or robotics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge