Connectivity structure and dynamics of nonlinear recurrent neural networks

We develop a theory to analyze how structure in connectivity shapes the high-dimensional, internally generated activity of nonlinear recurrent neural networks. Using two complementary methods -- a path-integral calculation of fluctuations around the saddle point, and a recently introduced two-site cavity approach -- we derive analytic expressions that characterize important features of collective activity, including its dimensionality and temporal correlations. To model structure in the coupling matrices of real neural circuits, such as synaptic connectomes obtained through electron microscopy, we introduce the random-mode model, which parameterizes a coupling matrix using random input and output modes and a specified spectrum. This model enables systematic study of the effects of low-dimensional structure in connectivity on neural activity. These effects manifest in features of collective activity, that we calculate, and can be undetectable when analyzing only single-neuron activities. We derive a relation between the effective rank of the coupling matrix and the dimension of activity. By extending the random-mode model, we compare the effects of single-neuron heterogeneity and low-dimensional connectivity. We also investigate the impact of structured overlaps between input and output modes, a feature of biological coupling matrices. Our theory provides tools to relate neural-network architecture and collective dynamics in artificial and biological systems.

A Unified Framework of Online Learning Algorithms for Training Recurrent Neural Networks

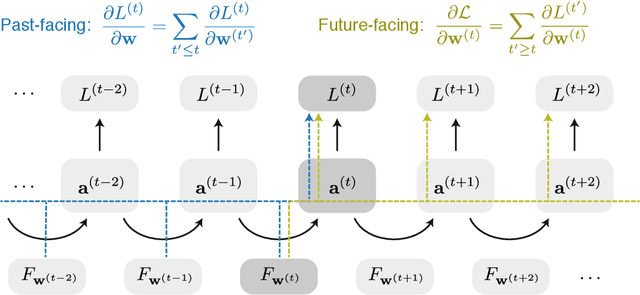
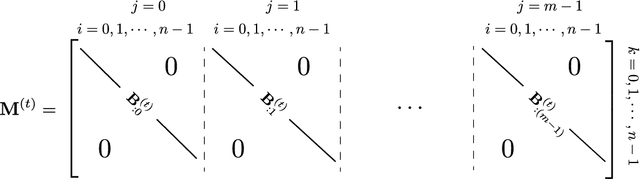
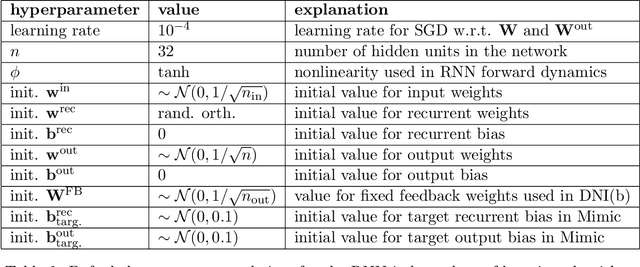
We present a framework for compactly summarizing many recent results in efficient and/or biologically plausible online training of recurrent neural networks (RNN). The framework organizes algorithms according to several criteria: (a) past vs. future facing, (b) tensor structure, (c) stochastic vs. deterministic, and (d) closed form vs. numerical. These axes reveal latent conceptual connections among several recent advances in online learning. Furthermore, we provide novel mathematical intuitions for their degree of success. Testing various algorithms on two synthetic tasks shows that performances cluster according to our criteria. Although a similar clustering is also observed for gradient alignment, alignment with exact methods does not alone explain ultimate performance, especially for stochastic algorithms. This suggests the need for better comparison metrics.

Using local plasticity rules to train recurrent neural networks

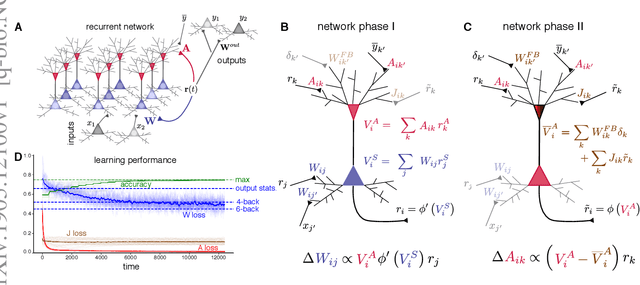
To learn useful dynamics on long time scales, neurons must use plasticity rules that account for long-term, circuit-wide effects of synaptic changes. In other words, neural circuits must solve a credit assignment problem to appropriately assign responsibility for global network behavior to individual circuit components. Furthermore, biological constraints demand that plasticity rules are spatially and temporally local; that is, synaptic changes can depend only on variables accessible to the pre- and postsynaptic neurons. While artificial intelligence offers a computational solution for credit assignment, namely backpropagation through time (BPTT), this solution is wildly biologically implausible. It requires both nonlocal computations and unlimited memory capacity, as any synaptic change is a complicated function of the entire history of network activity. Similar nonlocality issues plague other approaches such as FORCE (Sussillo et al. 2009). Overall, we are still missing a model for learning in recurrent circuits that both works computationally and uses only local updates. Leveraging recent advances in machine learning on approximating gradients for BPTT, we derive biologically plausible plasticity rules that enable recurrent networks to accurately learn long-term dependencies in sequential data. The solution takes the form of neurons with segregated voltage compartments, with several synaptic sub-populations that have different functional properties. The network operates in distinct phases during which each synaptic sub-population is updated by its own local plasticity rule. Our results provide new insights into the potential roles of segregated dendritic compartments, branch-specific inhibition, and global circuit phases in learning.