Using local plasticity rules to train recurrent neural networks
Paper and Code
May 28, 2019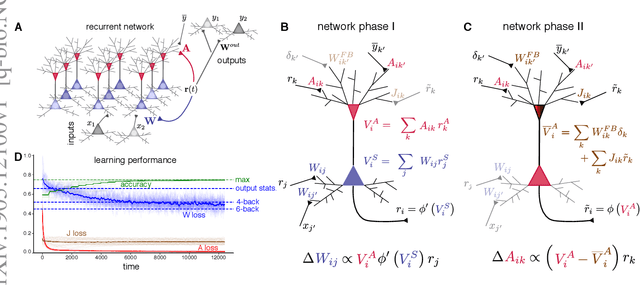
To learn useful dynamics on long time scales, neurons must use plasticity rules that account for long-term, circuit-wide effects of synaptic changes. In other words, neural circuits must solve a credit assignment problem to appropriately assign responsibility for global network behavior to individual circuit components. Furthermore, biological constraints demand that plasticity rules are spatially and temporally local; that is, synaptic changes can depend only on variables accessible to the pre- and postsynaptic neurons. While artificial intelligence offers a computational solution for credit assignment, namely backpropagation through time (BPTT), this solution is wildly biologically implausible. It requires both nonlocal computations and unlimited memory capacity, as any synaptic change is a complicated function of the entire history of network activity. Similar nonlocality issues plague other approaches such as FORCE (Sussillo et al. 2009). Overall, we are still missing a model for learning in recurrent circuits that both works computationally and uses only local updates. Leveraging recent advances in machine learning on approximating gradients for BPTT, we derive biologically plausible plasticity rules that enable recurrent networks to accurately learn long-term dependencies in sequential data. The solution takes the form of neurons with segregated voltage compartments, with several synaptic sub-populations that have different functional properties. The network operates in distinct phases during which each synaptic sub-population is updated by its own local plasticity rule. Our results provide new insights into the potential roles of segregated dendritic compartments, branch-specific inhibition, and global circuit phases in learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge