Coding schemes in neural networks learning classification tasks
Paper and Code
Jun 24, 2024

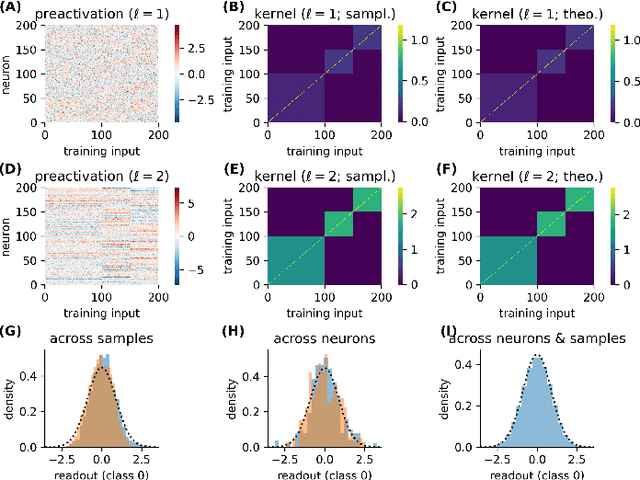
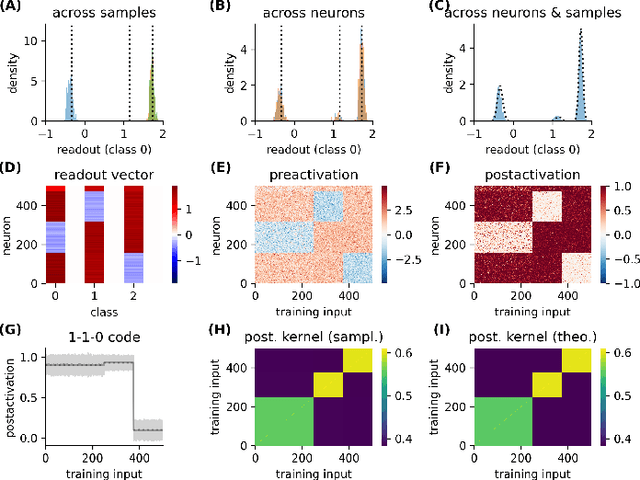
Neural networks posses the crucial ability to generate meaningful representations of task-dependent features. Indeed, with appropriate scaling, supervised learning in neural networks can result in strong, task-dependent feature learning. However, the nature of the emergent representations, which we call the `coding scheme', is still unclear. To understand the emergent coding scheme, we investigate fully-connected, wide neural networks learning classification tasks using the Bayesian framework where learning shapes the posterior distribution of the network weights. Consistent with previous findings, our analysis of the feature learning regime (also known as `non-lazy', `rich', or `mean-field' regime) shows that the networks acquire strong, data-dependent features. Surprisingly, the nature of the internal representations depends crucially on the neuronal nonlinearity. In linear networks, an analog coding scheme of the task emerges. Despite the strong representations, the mean predictor is identical to the lazy case. In nonlinear networks, spontaneous symmetry breaking leads to either redundant or sparse coding schemes. Our findings highlight how network properties such as scaling of weights and neuronal nonlinearity can profoundly influence the emergent representations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge