Separation of scales and a thermodynamic description of feature learning in some CNNs

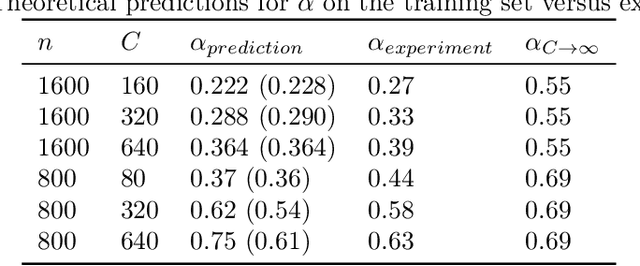
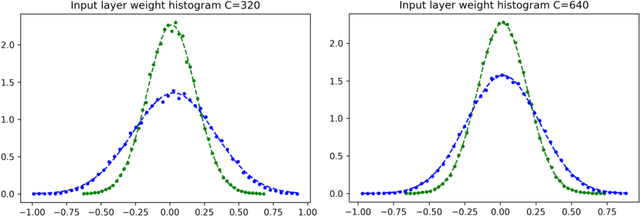
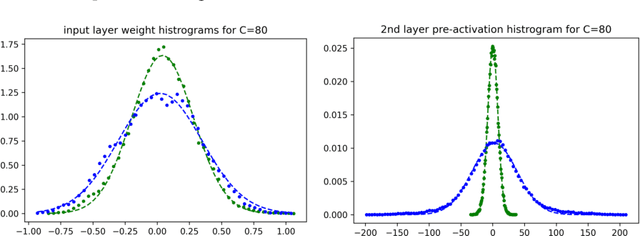
Deep neural networks (DNNs) are powerful tools for compressing and distilling information. Due to their scale and complexity, often involving billions of inter-dependent internal degrees of freedom, exact analysis approaches often fall short. A common strategy in such cases is to identify slow degrees of freedom that average out the erratic behavior of the underlying fast microscopic variables. Here, we identify such a separation of scales occurring in over-parameterized deep convolutional neural networks (CNNs) at the end of training. It implies that neuron pre-activations fluctuate in a nearly Gaussian manner with a deterministic latent kernel. While for CNNs with infinitely many channels these kernels are inert, for finite CNNs they adapt and learn from data in an analytically tractable manner. The resulting thermodynamic theory of deep learning yields accurate predictions on several deep non-linear CNN toy models. In addition, it provides new ways of analyzing and understanding CNNs.