Predictive Coding Networks and Inference Learning: Tutorial and Survey

Recent years have witnessed a growing call for renewed emphasis on neuroscience-inspired approaches in artificial intelligence research, under the banner of $\textit{NeuroAI}$. This is exemplified by recent attention gained by predictive coding networks (PCNs) within machine learning (ML). PCNs are based on the neuroscientific framework of predictive coding (PC), which views the brain as a hierarchical Bayesian inference model that minimizes prediction errors from feedback connections. PCNs trained with inference learning (IL) have potential advantages to traditional feedforward neural networks (FNNs) trained with backpropagation. While historically more computationally intensive, recent improvements in IL have shown that it can be more efficient than backpropagation with sufficient parallelization, making PCNs promising alternatives for large-scale applications and neuromorphic hardware. Moreover, PCNs can be mathematically considered as a superset of traditional FNNs, which substantially extends the range of possible architectures for both supervised and unsupervised learning. In this work, we provide a comprehensive review as well as a formal specification of PCNs, in particular placing them in the context of modern ML methods, and positioning PC as a versatile and promising framework worthy of further study by the ML community.

Opening the Black Box: predicting the trainability of deep neural networks with reconstruction entropy

An important challenge in machine learning is to predict the initial conditions under which a given neural network will be trainable. We present a method for predicting the trainable regime in parameter space for deep feedforward neural networks, based on reconstructing the input from subsequent activation layers via a cascade of single-layer auxiliary networks. For both MNIST and CIFAR10, we show that a single epoch of training of the shallow cascade networks is sufficient to predict the trainability of the deep feedforward network, thereby providing a significant reduction in overall training time. We achieve this by computing the relative entropy between reconstructed images and the original inputs, and show that this probe of information loss is sensitive to the phase behaviour of the network. Our results provide a concrete link between the flow of information and the trainability of deep neural networks, further elucidating the role of criticality in these systems.

Wilsonian Renormalization of Neural Network Gaussian Processes

Separating relevant and irrelevant information is key to any modeling process or scientific inquiry. Theoretical physics offers a powerful tool for achieving this in the form of the renormalization group (RG). Here we demonstrate a practical approach to performing Wilsonian RG in the context of Gaussian Process (GP) Regression. We systematically integrate out the unlearnable modes of the GP kernel, thereby obtaining an RG flow of the Gaussian Process in which the data plays the role of the energy scale. In simple cases, this results in a universal flow of the ridge parameter, which becomes input-dependent in the richer scenario in which non-Gaussianities are included. In addition to being analytically tractable, this approach goes beyond structural analogies between RG and neural networks by providing a natural connection between RG flow and learnable vs. unlearnable modes. Studying such flows may improve our understanding of feature learning in deep neural networks, and identify potential universality classes in these models.

Criticality versus uniformity in deep neural networks

Deep feedforward networks initialized along the edge of chaos exhibit exponentially superior training ability as quantified by maximum trainable depth. In this work, we explore the effect of saturation of the tanh activation function along the edge of chaos. In particular, we determine the line of uniformity in phase space along which the post-activation distribution has maximum entropy. This line intersects the edge of chaos, and indicates the regime beyond which saturation of the activation function begins to impede training efficiency. Our results suggest that initialization along the edge of chaos is a necessary but not sufficient condition for optimal trainability.

The edge of chaos: quantum field theory and deep neural networks

We explicitly construct the quantum field theory corresponding to a general class of deep neural networks encompassing both recurrent and feedforward architectures. We first consider the mean-field theory (MFT) obtained as the leading saddlepoint in the action, and derive the condition for criticality via the largest Lyapunov exponent. We then compute the loop corrections to the correlation function in a perturbative expansion in the ratio of depth $T$ to width $N$, and find a precise analogy with the well-studied $O(N)$ vector model, in which the variance of the weight initializations plays the role of the 't Hooft coupling. In particular, we compute both the $\mathcal{O}(1)$ corrections quantifying fluctuations from typicality in the ensemble of networks, and the subleading $\mathcal{O}(T/N)$ corrections due to finite-width effects. These provide corrections to the correlation length that controls the depth to which information can propagate through the network, and thereby sets the scale at which such networks are trainable by gradient descent. Our analysis provides a first-principles approach to the rapidly emerging NN-QFT correspondence, and opens several interesting avenues to the study of criticality in deep neural networks.

Towards quantifying information flows: relative entropy in deep neural networks and the renormalization group

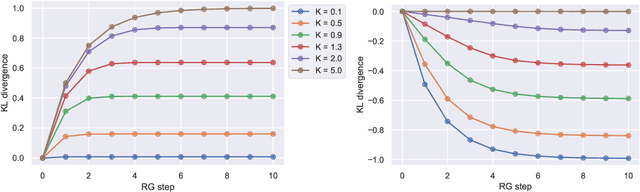
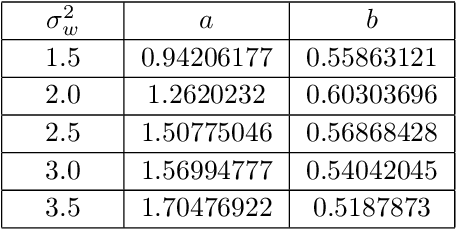
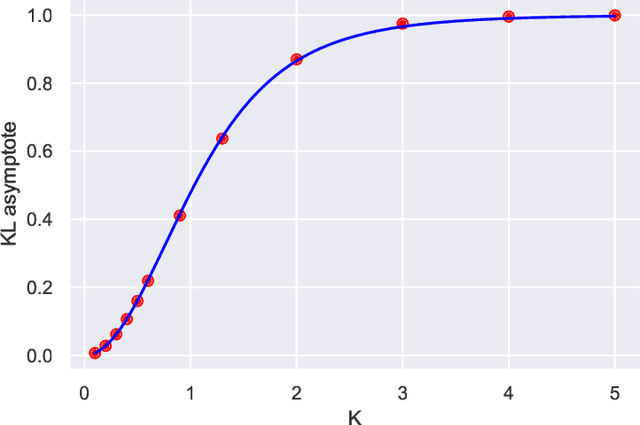
We investigate the analogy between the renormalization group (RG) and deep neural networks, wherein subsequent layers of neurons are analogous to successive steps along the RG. In particular, we quantify the flow of information by explicitly computing the relative entropy or Kullback-Leibler divergence in both the one- and two-dimensional Ising models under decimation RG, as well as in a feedforward neural network as a function of depth. We observe qualitatively identical behavior characterized by the monotonic increase to a parameter-dependent asymptotic value. On the quantum field theory side, the monotonic increase confirms the connection between the relative entropy and the c-theorem. For the neural networks, the asymptotic behavior may have implications for various information maximization methods in machine learning, as well as for disentangling compactness and generalizability. Furthermore, while both the two-dimensional Ising model and the random neural networks we consider exhibit non-trivial critical points, the relative entropy appears insensitive to the phase structure of either system. In this sense, more refined probes are required in order to fully elucidate the flow of information in these models.