Opening the Black Box: predicting the trainability of deep neural networks with reconstruction entropy

An important challenge in machine learning is to predict the initial conditions under which a given neural network will be trainable. We present a method for predicting the trainable regime in parameter space for deep feedforward neural networks, based on reconstructing the input from subsequent activation layers via a cascade of single-layer auxiliary networks. For both MNIST and CIFAR10, we show that a single epoch of training of the shallow cascade networks is sufficient to predict the trainability of the deep feedforward network, thereby providing a significant reduction in overall training time. We achieve this by computing the relative entropy between reconstructed images and the original inputs, and show that this probe of information loss is sensitive to the phase behaviour of the network. Our results provide a concrete link between the flow of information and the trainability of deep neural networks, further elucidating the role of criticality in these systems.

Towards quantifying information flows: relative entropy in deep neural networks and the renormalization group

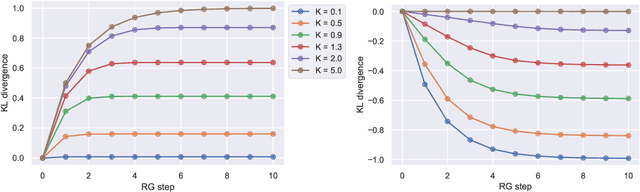
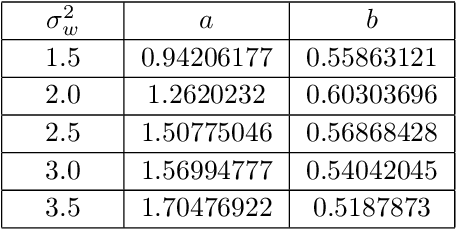
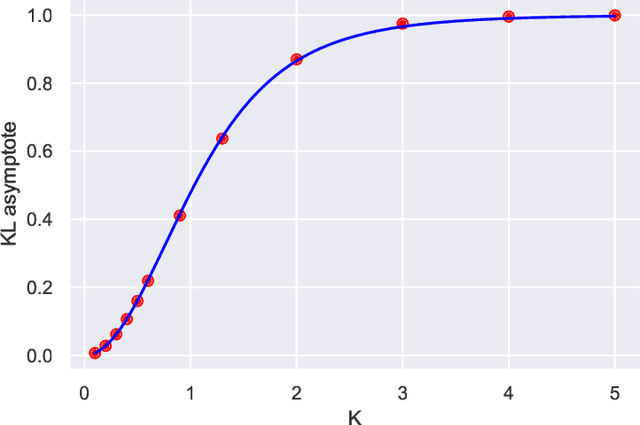
We investigate the analogy between the renormalization group (RG) and deep neural networks, wherein subsequent layers of neurons are analogous to successive steps along the RG. In particular, we quantify the flow of information by explicitly computing the relative entropy or Kullback-Leibler divergence in both the one- and two-dimensional Ising models under decimation RG, as well as in a feedforward neural network as a function of depth. We observe qualitatively identical behavior characterized by the monotonic increase to a parameter-dependent asymptotic value. On the quantum field theory side, the monotonic increase confirms the connection between the relative entropy and the c-theorem. For the neural networks, the asymptotic behavior may have implications for various information maximization methods in machine learning, as well as for disentangling compactness and generalizability. Furthermore, while both the two-dimensional Ising model and the random neural networks we consider exhibit non-trivial critical points, the relative entropy appears insensitive to the phase structure of either system. In this sense, more refined probes are required in order to fully elucidate the flow of information in these models.