A self consistent theory of Gaussian Processes captures feature learning effects in finite CNNs

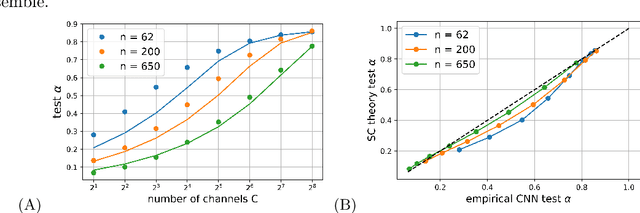
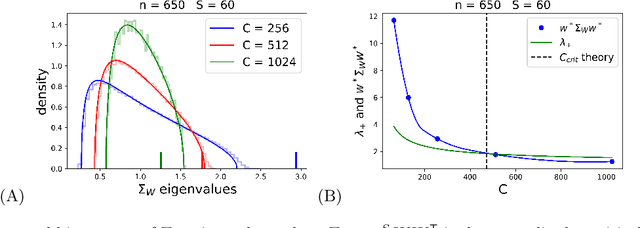
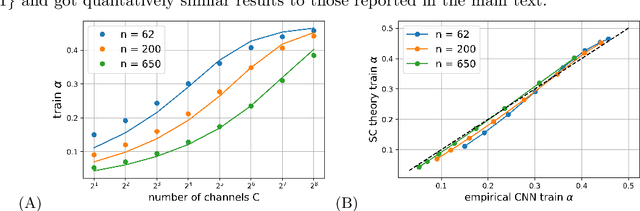
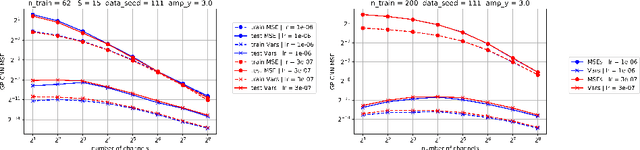
Deep neural networks (DNNs) in the infinite width/channel limit have received much attention recently, as they provide a clear analytical window to deep learning via mappings to Gaussian Processes (GPs). Despite its theoretical appeal, this viewpoint lacks a crucial ingredient of deep learning in finite DNNs, laying at the heart of their success -- feature learning. Here we consider DNNs trained with noisy gradient descent on a large training set and derive a self consistent Gaussian Process theory accounting for strong finite-DNN and feature learning effects. Applying this to a toy model of a two-layer linear convolutional neural network (CNN) shows good agreement with experiments. We further identify, both analytical and numerically, a sharp transition between a feature learning regime and a lazy learning regime in this model. Strong finite-DNN effects are also derived for a non-linear two-layer fully connected network. Our self consistent theory provides a rich and versatile analytical framework for studying feature learning and other non-lazy effects in finite DNNs.

Predicting the outputs of finite networks trained with noisy gradients

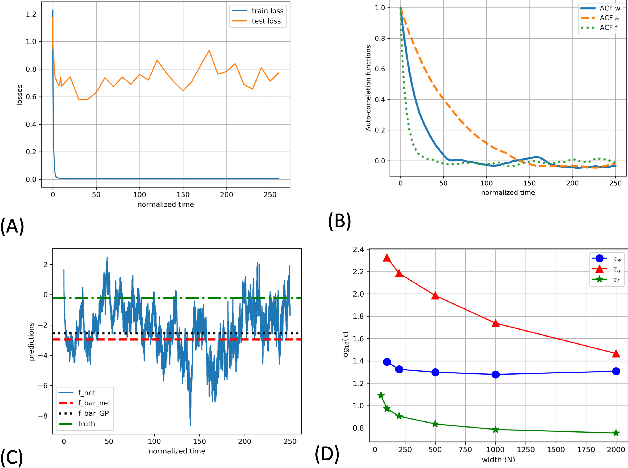
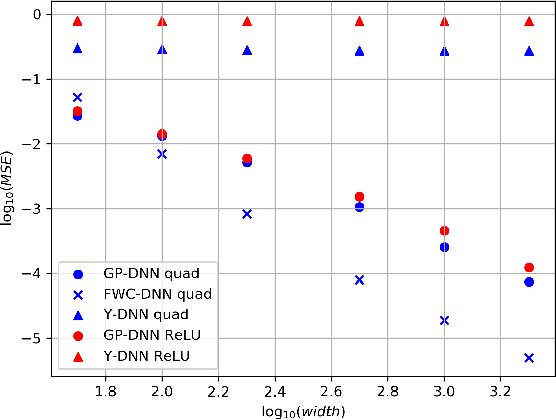
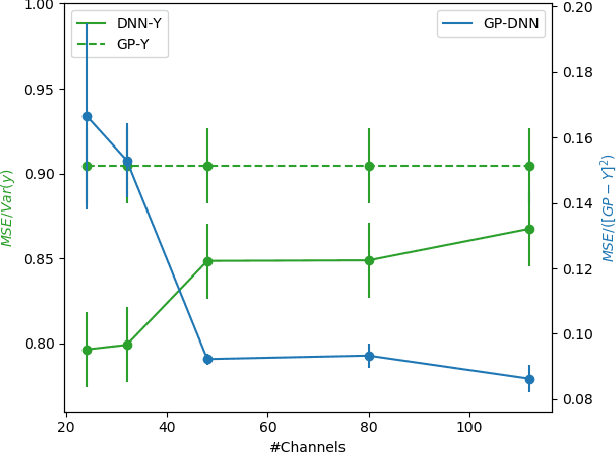
A recent line of studies has focused on the infinite width limit of deep neural networks (DNNs) where, under a certain deterministic training protocol, the DNN outputs are related to a Gaussian Process (GP) known as the Neural Tangent Kernel (NTK). However, finite-width DNNs differ from GPs quantitatively and for CNNs the difference may be qualitative. Here we present a DNN training protocol involving noise whose outcome is mappable to a certain non-Gaussian stochastic process. An analytical framework is then introduced to analyze this resulting non-Gaussian process, whose deviation from a GP is controlled by the finite width. Our work extends upon previous relations between DNNs and GPs in several ways: (a) In the infinite width limit, it establishes a mapping between DNNs and a GP different from the NTK. (b) It allows computing analytically the general form of the finite width correction (FWC) for DNNs with arbitrary activation functions and depth and further provides insight on the magnitude and implications of these FWCs. (c) It appears capable of providing better performance than the corresponding GP in the case of CNNs. We are able to predict the outputs of empirical finite networks with high accuracy, improving upon the accuracy of GP predictions by over an order of magnitude. Overall, we provide a framework that offers both an analytical handle and a more faithful model of real-world settings than previous studies in this avenue of research.