Understanding How Encoder-Decoder Architectures Attend

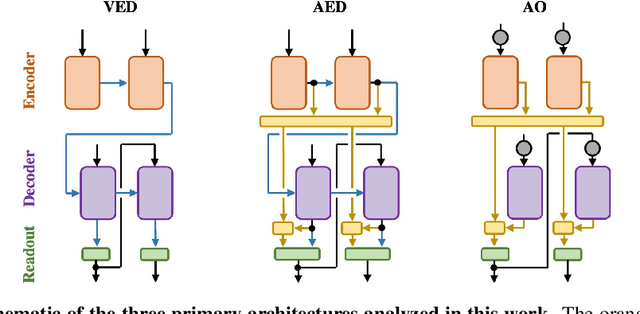
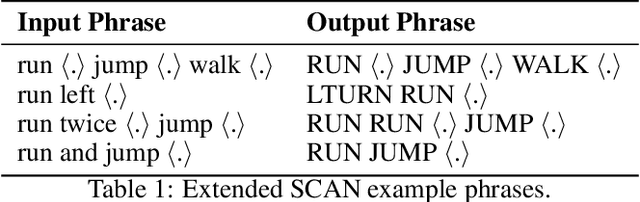
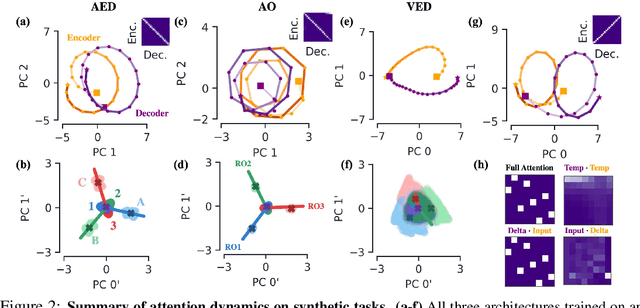
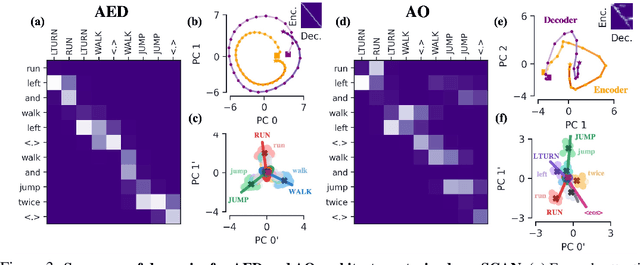
Encoder-decoder networks with attention have proven to be a powerful way to solve many sequence-to-sequence tasks. In these networks, attention aligns encoder and decoder states and is often used for visualizing network behavior. However, the mechanisms used by networks to generate appropriate attention matrices are still mysterious. Moreover, how these mechanisms vary depending on the particular architecture used for the encoder and decoder (recurrent, feed-forward, etc.) are also not well understood. In this work, we investigate how encoder-decoder networks solve different sequence-to-sequence tasks. We introduce a way of decomposing hidden states over a sequence into temporal (independent of input) and input-driven (independent of sequence position) components. This reveals how attention matrices are formed: depending on the task requirements, networks rely more heavily on either the temporal or input-driven components. These findings hold across both recurrent and feed-forward architectures despite their differences in forming the temporal components. Overall, our results provide new insight into the inner workings of attention-based encoder-decoder networks.

The geometry of integration in text classification RNNs

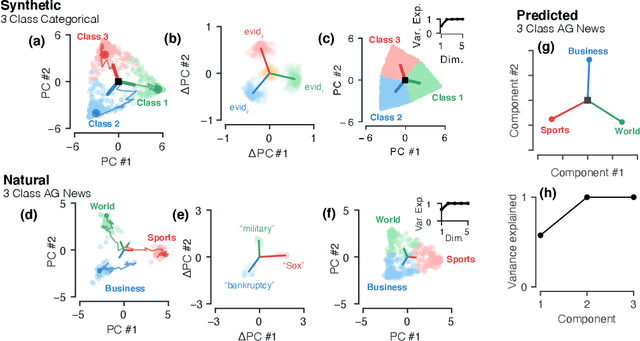
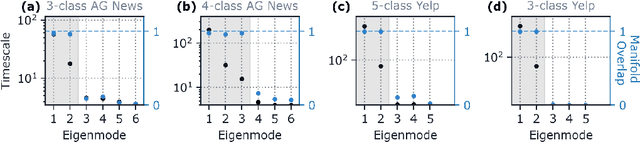
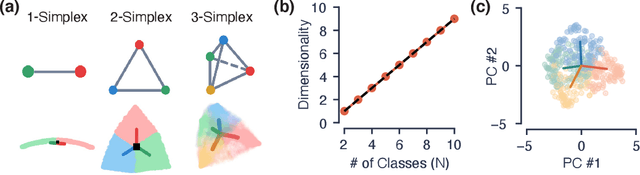
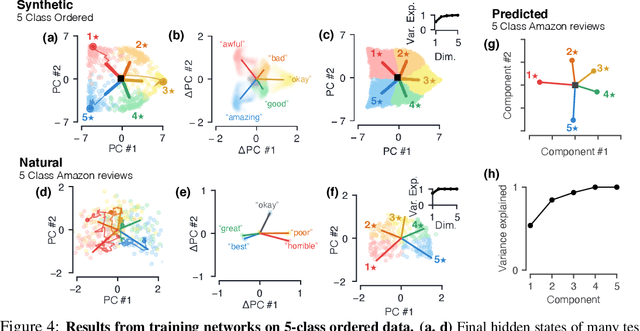
Despite the widespread application of recurrent neural networks (RNNs) across a variety of tasks, a unified understanding of how RNNs solve these tasks remains elusive. In particular, it is unclear what dynamical patterns arise in trained RNNs, and how those patterns depend on the training dataset or task. This work addresses these questions in the context of a specific natural language processing task: text classification. Using tools from dynamical systems analysis, we study recurrent networks trained on a battery of both natural and synthetic text classification tasks. We find the dynamics of these trained RNNs to be both interpretable and low-dimensional. Specifically, across architectures and datasets, RNNs accumulate evidence for each class as they process the text, using a low-dimensional attractor manifold as the underlying mechanism. Moreover, the dimensionality and geometry of the attractor manifold are determined by the structure of the training dataset; in particular, we describe how simple word-count statistics computed on the training dataset can be used to predict these properties. Our observations span multiple architectures and datasets, reflecting a common mechanism RNNs employ to perform text classification. To the degree that integration of evidence towards a decision is a common computational primitive, this work lays the foundation for using dynamical systems techniques to study the inner workings of RNNs.

On the asymptotics of wide networks with polynomial activations

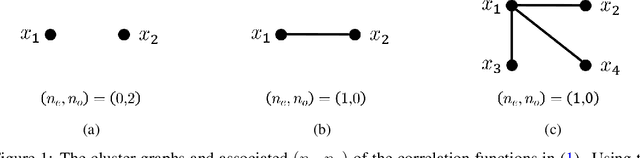
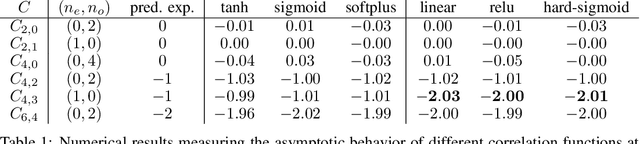
We consider an existing conjecture addressing the asymptotic behavior of neural networks in the large width limit. The results that follow from this conjecture include tight bounds on the behavior of wide networks during stochastic gradient descent, and a derivation of their finite-width dynamics. We prove the conjecture for deep networks with polynomial activation functions, greatly extending the validity of these results. Finally, we point out a difference in the asymptotic behavior of networks with analytic (and non-linear) activation functions and those with piecewise-linear activations such as ReLU.