Bounding generalization error with input compression: An empirical study with infinite-width networks
Paper and Code
Jul 19, 2022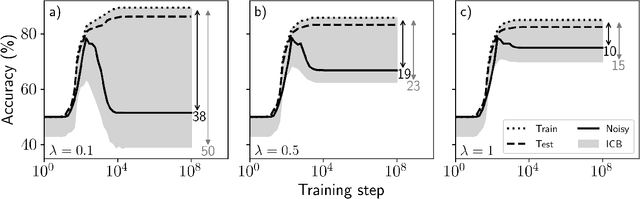

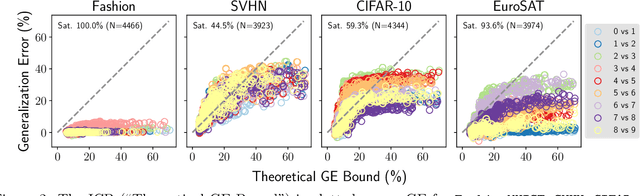
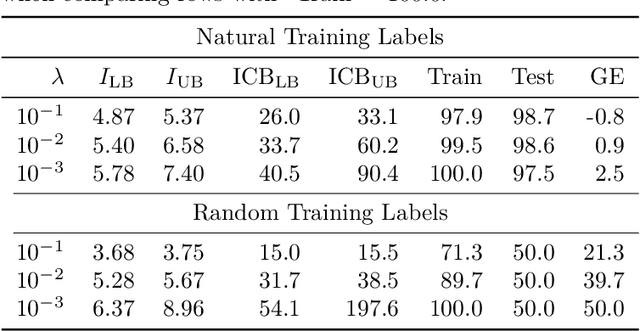
Estimating the Generalization Error (GE) of Deep Neural Networks (DNNs) is an important task that often relies on availability of held-out data. The ability to better predict GE based on a single training set may yield overarching DNN design principles to reduce a reliance on trial-and-error, along with other performance assessment advantages. In search of a quantity relevant to GE, we investigate the Mutual Information (MI) between the input and final layer representations, using the infinite-width DNN limit to bound MI. An existing input compression-based GE bound is used to link MI and GE. To the best of our knowledge, this represents the first empirical study of this bound. In our attempt to empirically falsify the theoretical bound, we find that it is often tight for best-performing models. Furthermore, it detects randomization of training labels in many cases, reflects test-time perturbation robustness, and works well given only few training samples. These results are promising given that input compression is broadly applicable where MI can be estimated with confidence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge