The Neural Covariance SDE: Shaped Infinite Depth-and-Width Networks at Initialization
Paper and Code
Jun 06, 2022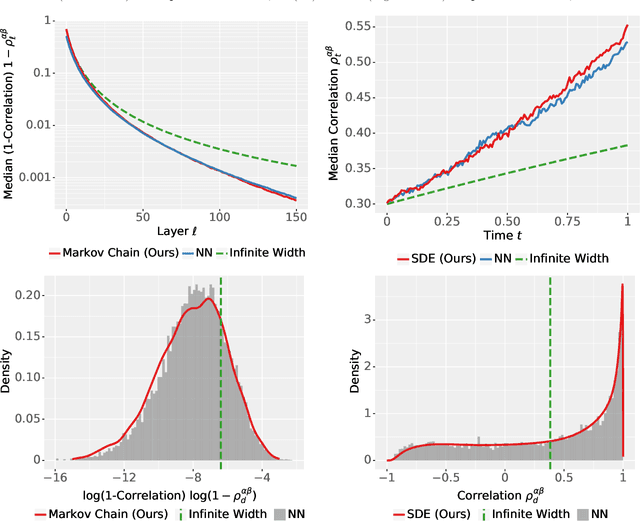

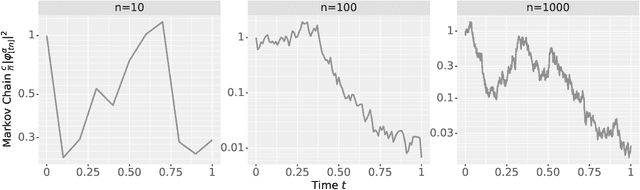
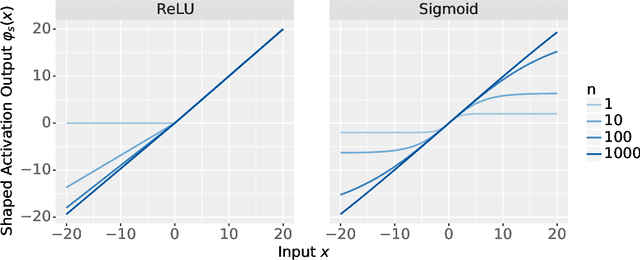
The logit outputs of a feedforward neural network at initialization are conditionally Gaussian, given a random covariance matrix defined by the penultimate layer. In this work, we study the distribution of this random matrix. Recent work has shown that shaping the activation function as network depth grows large is necessary for this covariance matrix to be non-degenerate. However, the current infinite-width-style understanding of this shaping method is unsatisfactory for large depth: infinite-width analyses ignore the microscopic fluctuations from layer to layer, but these fluctuations accumulate over many layers. To overcome this shortcoming, we study the random covariance matrix in the shaped infinite-depth-and-width limit. We identify the precise scaling of the activation function necessary to arrive at a non-trivial limit, and show that the random covariance matrix is governed by a stochastic differential equation (SDE) that we call the Neural Covariance SDE. Using simulations, we show that the SDE closely matches the distribution of the random covariance matrix of finite networks. Additionally, we recover an if-and-only-if condition for exploding and vanishing norms of large shaped networks based on the activation function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge