Preserving linear invariants in ensemble filtering methods

Formulating dynamical models for physical phenomena is essential for understanding the interplay between the different mechanisms and predicting the evolution of physical states. However, a dynamical model alone is often insufficient to address these fundamental tasks, as it suffers from model errors and uncertainties. One common remedy is to rely on data assimilation, where the state estimate is updated with observations of the true system. Ensemble filters sequentially assimilate observations by updating a set of samples over time. They operate in two steps: a forecast step that propagates each sample through the dynamical model and an analysis step that updates the samples with incoming observations. For accurate and robust predictions of dynamical systems, discrete solutions must preserve their critical invariants. While modern numerical solvers satisfy these invariants, existing invariant-preserving analysis steps are limited to Gaussian settings and are often not compatible with classical regularization techniques of ensemble filters, e.g., inflation and covariance tapering. The present work focuses on preserving linear invariants, such as mass, stoichiometric balance of chemical species, and electrical charges. Using tools from measure transport theory (Spantini et al., 2022, SIAM Review), we introduce a generic class of nonlinear ensemble filters that automatically preserve desired linear invariants in non-Gaussian filtering problems. By specializing this framework to the Gaussian setting, we recover a constrained formulation of the Kalman filter. Then, we show how to combine existing regularization techniques for the ensemble Kalman filter (Evensen, 1994, J. Geophys. Res.) with the preservation of the linear invariants. Finally, we assess the benefits of preserving linear invariants for the ensemble Kalman filter and nonlinear ensemble filters.

Leveraging joint sparsity in hierarchical Bayesian learning

We present a hierarchical Bayesian learning approach to infer jointly sparse parameter vectors from multiple measurement vectors. Our model uses separate conditionally Gaussian priors for each parameter vector and common gamma-distributed hyper-parameters to enforce joint sparsity. The resulting joint-sparsity-promoting priors are combined with existing Bayesian inference methods to generate a new family of algorithms. Our numerical experiments, which include a multi-coil magnetic resonance imaging application, demonstrate that our new approach consistently outperforms commonly used hierarchical Bayesian methods.

Sequential image recovery using joint hierarchical Bayesian learning

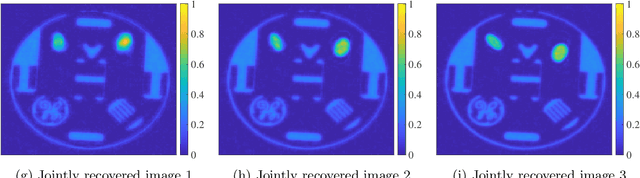
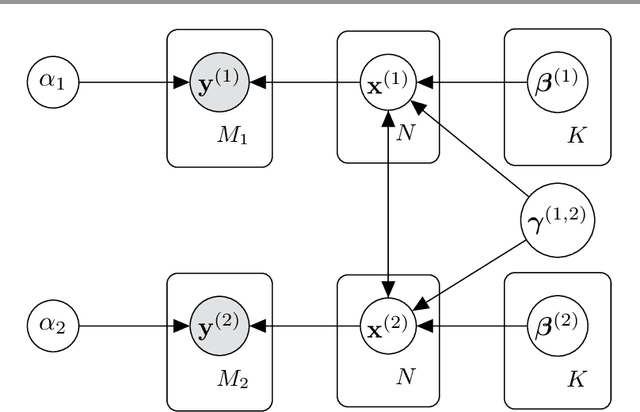
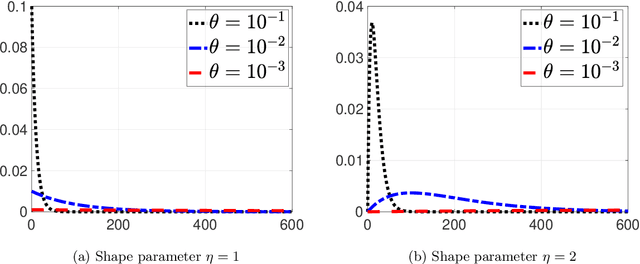
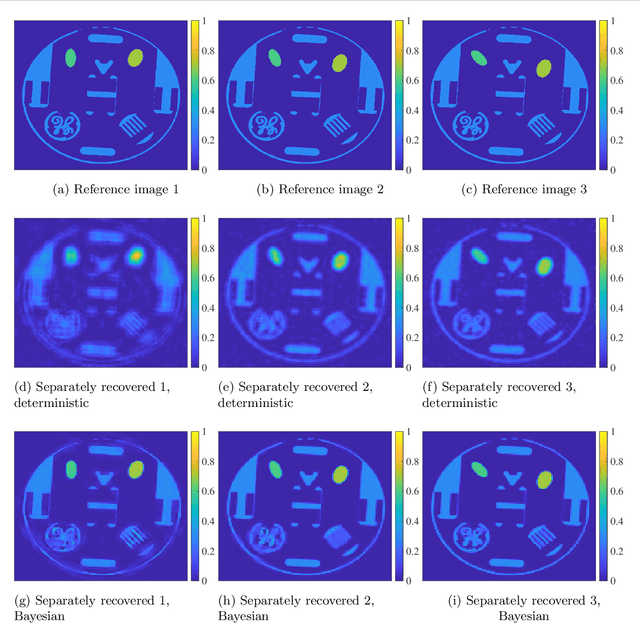
Recovering temporal image sequences (videos) based on indirect, noisy, or incomplete data is an essential yet challenging task. We specifically consider the case where each data set is missing vital information, which prevents the accurate recovery of the individual images. Although some recent (variational) methods have demonstrated high-resolution image recovery based on jointly recovering sequential images, there remain robustness issues due to parameter tuning and restrictions on the type of the sequential images. Here, we present a method based on hierarchical Bayesian learning for the joint recovery of sequential images that incorporates prior intra- and inter-image information. Our method restores the missing information in each image by "borrowing" it from the other images. As a result, \emph{all} of the individual reconstructions yield improved accuracy. Our method can be used for various data acquisitions and allows for uncertainty quantification. Some preliminary results indicate its potential use for sequential deblurring and magnetic resonance imaging.