A friendly introduction to triangular transport

Decision making under uncertainty is a cross-cutting challenge in science and engineering. Most approaches to this challenge employ probabilistic representations of uncertainty. In complicated systems accessible only via data or black-box models, however, these representations are rarely known. We discuss how to characterize and manipulate such representations using triangular transport maps, which approximate any complex probability distribution as a transformation of a simple, well-understood distribution. The particular structure of triangular transport guarantees many desirable mathematical and computational properties that translate well into solving practical problems. Triangular maps are actively used for density estimation, (conditional) generative modelling, Bayesian inference, data assimilation, optimal experimental design, and related tasks. While there is ample literature on the development and theory of triangular transport methods, this manuscript provides a detailed introduction for scientists interested in employing measure transport without assuming a formal mathematical background. We build intuition for the key foundations of triangular transport, discuss many aspects of its practical implementation, and outline the frontiers of this field.

Preserving linear invariants in ensemble filtering methods

Formulating dynamical models for physical phenomena is essential for understanding the interplay between the different mechanisms and predicting the evolution of physical states. However, a dynamical model alone is often insufficient to address these fundamental tasks, as it suffers from model errors and uncertainties. One common remedy is to rely on data assimilation, where the state estimate is updated with observations of the true system. Ensemble filters sequentially assimilate observations by updating a set of samples over time. They operate in two steps: a forecast step that propagates each sample through the dynamical model and an analysis step that updates the samples with incoming observations. For accurate and robust predictions of dynamical systems, discrete solutions must preserve their critical invariants. While modern numerical solvers satisfy these invariants, existing invariant-preserving analysis steps are limited to Gaussian settings and are often not compatible with classical regularization techniques of ensemble filters, e.g., inflation and covariance tapering. The present work focuses on preserving linear invariants, such as mass, stoichiometric balance of chemical species, and electrical charges. Using tools from measure transport theory (Spantini et al., 2022, SIAM Review), we introduce a generic class of nonlinear ensemble filters that automatically preserve desired linear invariants in non-Gaussian filtering problems. By specializing this framework to the Gaussian setting, we recover a constrained formulation of the Kalman filter. Then, we show how to combine existing regularization techniques for the ensemble Kalman filter (Evensen, 1994, J. Geophys. Res.) with the preservation of the linear invariants. Finally, we assess the benefits of preserving linear invariants for the ensemble Kalman filter and nonlinear ensemble filters.

An adaptive ensemble filter for heavy-tailed distributions: tuning-free inflation and localization

Heavy tails is a common feature of filtering distributions that results from the nonlinear dynamical and observation processes as well as the uncertainty from physical sensors. In these settings, the Kalman filter and its ensemble version - the ensemble Kalman filter (EnKF) - that have been designed under Gaussian assumptions result in degraded performance. t-distributions are a parametric family of distributions whose tail-heaviness is modulated by a degree of freedom $\nu$. Interestingly, Cauchy and Gaussian distributions correspond to the extreme cases of a t-distribution for $\nu = 1$ and $\nu = \infty$, respectively. Leveraging tools from measure transport (Spantini et al., SIAM Review, 2022), we present a generalization of the EnKF whose prior-to-posterior update leads to exact inference for t-distributions. We demonstrate that this filter is less sensitive to outlying synthetic observations generated by the observation model for small $\nu$. Moreover, it recovers the Kalman filter for $\nu = \infty$. For nonlinear state-space models with heavy-tailed noise, we propose an algorithm to estimate the prior-to-posterior update from samples of joint forecast distribution of the states and observations. We rely on a regularized expectation-maximization (EM) algorithm to estimate the mean, scale matrix, and degree of freedom of heavy-tailed \textit{t}-distributions from limited samples (Finegold and Drton, arXiv preprint, 2014). Leveraging the conditional independence of the joint forecast distribution, we regularize the scale matrix with an $l1$ sparsity-promoting penalization of the log-likelihood at each iteration of the EM algorithm. By sequentially estimating the degree of freedom at each analysis step, our filter can adapt its prior-to-posterior update to the tail-heaviness of the data. We demonstrate the benefits of this new ensemble filter on challenging filtering problems.

A low-rank ensemble Kalman filter for elliptic observations

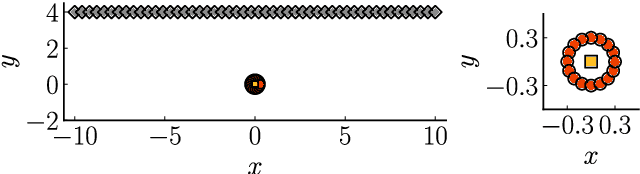
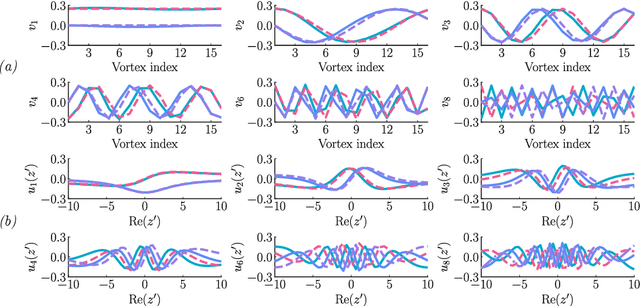
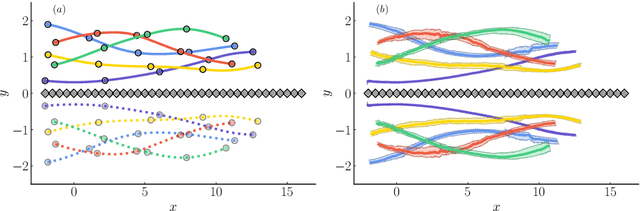
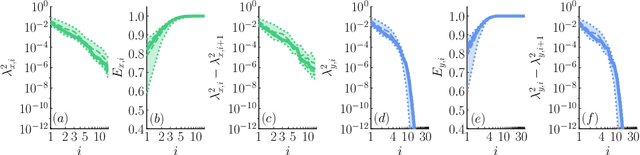
We propose a regularization method for ensemble Kalman filtering (EnKF) with elliptic observation operators. Commonly used EnKF regularization methods suppress state correlations at long distances. For observations described by elliptic partial differential equations, such as the pressure Poisson equation (PPE) in incompressible fluid flows, distance localization cannot be applied, as we cannot disentangle slowly decaying physical interactions from spurious long-range correlations. This is particularly true for the PPE, in which distant vortex elements couple nonlinearly to induce pressure. Instead, these inverse problems have a low effective dimension: low-dimensional projections of the observations strongly inform a low-dimensional subspace of the state space. We derive a low-rank factorization of the Kalman gain based on the spectrum of the Jacobian of the observation operator. The identified eigenvectors generalize the source and target modes of the multipole expansion, independently of the underlying spatial distribution of the problem. Given rapid spectral decay, inference can be performed in the low-dimensional subspace spanned by the dominant eigenvectors. This low-rank EnKF is assessed on dynamical systems with Poisson observation operators, where we seek to estimate the positions and strengths of point singularities over time from potential or pressure observations. We also comment on the broader applicability of this approach to elliptic inverse problems outside the context of filtering.