Quantification and Classification of Carbon Nanotubes in Electron Micrographs using Vision Foundation Models

Accurate characterization of carbon nanotube morphologies in electron microscopy images is vital for exposure assessment and toxicological studies, yet current workflows rely on slow, subjective manual segmentation. This work presents a unified framework leveraging vision foundation models to automate the quantification and classification of CNTs in electron microscopy images. First, we introduce an interactive quantification tool built on the Segment Anything Model (SAM) that segments particles with near-perfect accuracy using minimal user input. Second, we propose a novel classification pipeline that utilizes these segmentation masks to spatially constrain a DINOv2 vision transformer, extracting features exclusively from particle regions while suppressing background noise. Evaluated on a dataset of 1,800 TEM images, this architecture achieves 95.5% accuracy in distinguishing between four different CNT morphologies, significantly outperforming the current baseline despite using a fraction of the training data. Crucially, this instance-level processing allows the framework to resolve mixed samples, correctly classifying distinct particle types co-existing within a single field of view. These results demonstrate that integrating zero-shot segmentation with self-supervised feature learning enables high-throughput, reproducible nanomaterial analysis, transforming a labor-intensive bottleneck into a scalable, data-driven process.

Attention on flow control: transformer-based reinforcement learning for lift regulation in highly disturbed flows

A linear flow control strategy designed for weak disturbances may not remain effective in sequences of strong disturbances due to nonlinear interactions, but it is sensible to leverage it for developing a better strategy. In the present study, we propose a transformer-based reinforcement learning (RL) framework to learn an effective control strategy for regulating aerodynamic lift in gust sequences via pitch control. The transformer addresses the challenge of partial observability from limited surface pressure sensors. We demonstrate that the training can be accelerated with two techniques -- pretraining with an expert policy (here, linear control) and task-level transfer learning (here, extending a policy trained on isolated gusts to multiple gusts). We show that the learned strategy outperforms the best proportional control, with the performance gap widening as the number of gusts increases. The control strategy learned in an environment with a small number of successive gusts is shown to effectively generalize to an environment with an arbitrarily long sequence of gusts. We investigate the pivot configuration and show that quarter-chord pitching control can achieve superior lift regulation with substantially less control effort compared to mid-chord pitching control. Through a decomposition of the lift, we attribute this advantage to the dominant added-mass contribution accessible via quarter-chord pitching. The success on multiple configurations shows the generalizability of the proposed transformer-based RL framework, which offers a promising approach to solve more computationally demanding flow control problems when combined with the proposed acceleration techniques.

Low-Order Flow Reconstruction and Uncertainty Quantification in Disturbed Aerodynamics Using Sparse Pressure Measurements

This paper presents a novel machine-learning framework for reconstructing low-order gust-encounter flow field and lift coefficients from sparse, noisy surface pressure measurements. Our study thoroughly investigates the time-varying response of sensors to gust-airfoil interactions, uncovering valuable insights into optimal sensor placement. To address uncertainties in deep learning predictions, we implement probabilistic regression strategies to model both epistemic and aleatoric uncertainties. Epistemic uncertainty, reflecting the model's confidence in its predictions, is modeled using Monte Carlo dropout, as an approximation to the variational inference in the Bayesian framework, treating the neural network as a stochastic entity. On the other hand, aleatoric uncertainty, arising from noisy input measurements, is captured via learned statistical parameters, which propagates measurement noise through the network into the final predictions. Our results showcase the efficacy of this dual uncertainty quantification strategy in accurately predicting aerodynamic behavior under extreme conditions while maintaining computational efficiency, underscoring its potential to improve online sensor-based flow estimation in real-world applications.

An adaptive ensemble filter for heavy-tailed distributions: tuning-free inflation and localization

Heavy tails is a common feature of filtering distributions that results from the nonlinear dynamical and observation processes as well as the uncertainty from physical sensors. In these settings, the Kalman filter and its ensemble version - the ensemble Kalman filter (EnKF) - that have been designed under Gaussian assumptions result in degraded performance. t-distributions are a parametric family of distributions whose tail-heaviness is modulated by a degree of freedom $\nu$. Interestingly, Cauchy and Gaussian distributions correspond to the extreme cases of a t-distribution for $\nu = 1$ and $\nu = \infty$, respectively. Leveraging tools from measure transport (Spantini et al., SIAM Review, 2022), we present a generalization of the EnKF whose prior-to-posterior update leads to exact inference for t-distributions. We demonstrate that this filter is less sensitive to outlying synthetic observations generated by the observation model for small $\nu$. Moreover, it recovers the Kalman filter for $\nu = \infty$. For nonlinear state-space models with heavy-tailed noise, we propose an algorithm to estimate the prior-to-posterior update from samples of joint forecast distribution of the states and observations. We rely on a regularized expectation-maximization (EM) algorithm to estimate the mean, scale matrix, and degree of freedom of heavy-tailed \textit{t}-distributions from limited samples (Finegold and Drton, arXiv preprint, 2014). Leveraging the conditional independence of the joint forecast distribution, we regularize the scale matrix with an $l1$ sparsity-promoting penalization of the log-likelihood at each iteration of the EM algorithm. By sequentially estimating the degree of freedom at each analysis step, our filter can adapt its prior-to-posterior update to the tail-heaviness of the data. We demonstrate the benefits of this new ensemble filter on challenging filtering problems.

A low-rank ensemble Kalman filter for elliptic observations

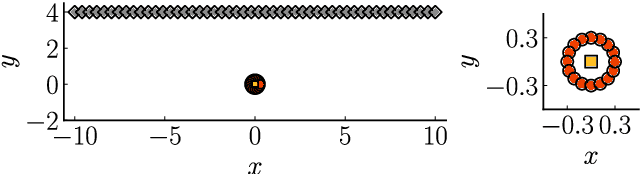
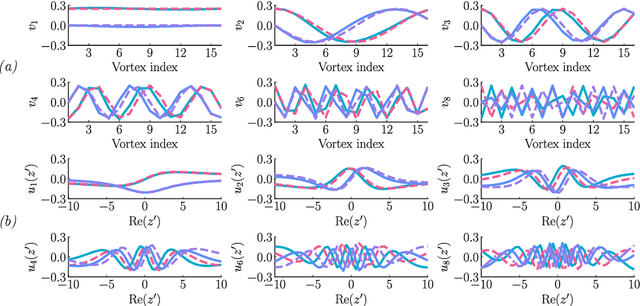
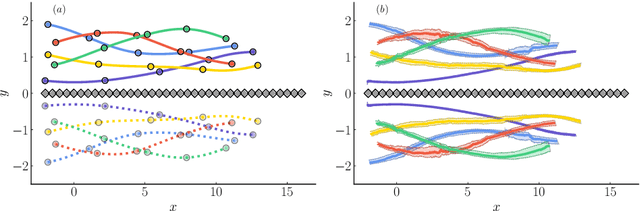
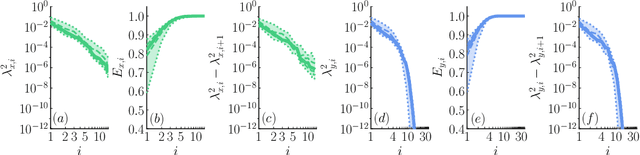
We propose a regularization method for ensemble Kalman filtering (EnKF) with elliptic observation operators. Commonly used EnKF regularization methods suppress state correlations at long distances. For observations described by elliptic partial differential equations, such as the pressure Poisson equation (PPE) in incompressible fluid flows, distance localization cannot be applied, as we cannot disentangle slowly decaying physical interactions from spurious long-range correlations. This is particularly true for the PPE, in which distant vortex elements couple nonlinearly to induce pressure. Instead, these inverse problems have a low effective dimension: low-dimensional projections of the observations strongly inform a low-dimensional subspace of the state space. We derive a low-rank factorization of the Kalman gain based on the spectrum of the Jacobian of the observation operator. The identified eigenvectors generalize the source and target modes of the multipole expansion, independently of the underlying spatial distribution of the problem. Given rapid spectral decay, inference can be performed in the low-dimensional subspace spanned by the dominant eigenvectors. This low-rank EnKF is assessed on dynamical systems with Poisson observation operators, where we seek to estimate the positions and strengths of point singularities over time from potential or pressure observations. We also comment on the broader applicability of this approach to elliptic inverse problems outside the context of filtering.