Uniform Convergence of Deep Neural Networks with Lipschitz Continuous Activation Functions and Variable Widths

We consider deep neural networks with a Lipschitz continuous activation function and with weight matrices of variable widths. We establish a uniform convergence analysis framework in which sufficient conditions on weight matrices and bias vectors together with the Lipschitz constant are provided to ensure uniform convergence of the deep neural networks to a meaningful function as the number of their layers tends to infinity. In the framework, special results on uniform convergence of deep neural networks with a fixed width, bounded widths and unbounded widths are presented. In particular, as convolutional neural networks are special deep neural networks with weight matrices of increasing widths, we put forward conditions on the mask sequence which lead to uniform convergence of resulting convolutional neural networks. The Lipschitz continuity assumption on the activation functions allows us to include in our theory most of commonly used activation functions in applications.

Dual Information Enhanced Multi-view Attributed Graph Clustering

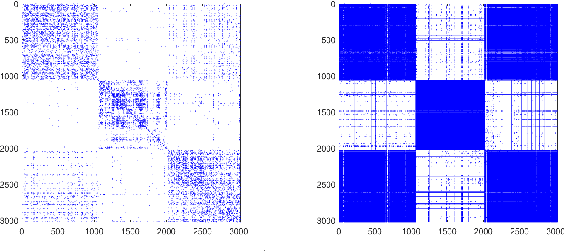
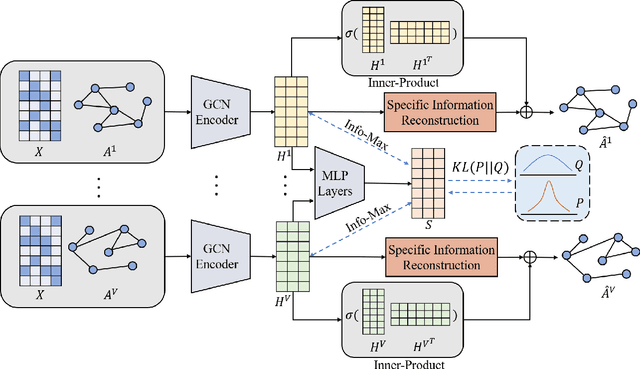
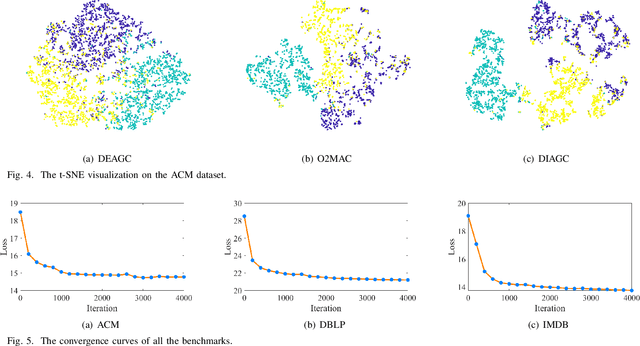
Multi-view attributed graph clustering is an important approach to partition multi-view data based on the attribute feature and adjacent matrices from different views. Some attempts have been made in utilizing Graph Neural Network (GNN), which have achieved promising clustering performance. Despite this, few of them pay attention to the inherent specific information embedded in multiple views. Meanwhile, they are incapable of recovering the latent high-level representation from the low-level ones, greatly limiting the downstream clustering performance. To fill these gaps, a novel Dual Information enhanced multi-view Attributed Graph Clustering (DIAGC) method is proposed in this paper. Specifically, the proposed method introduces the Specific Information Reconstruction (SIR) module to disentangle the explorations of the consensus and specific information from multiple views, which enables GCN to capture the more essential low-level representations. Besides, the Mutual Information Maximization (MIM) module maximizes the agreement between the latent high-level representation and low-level ones, and enables the high-level representation to satisfy the desired clustering structure with the help of the Self-supervised Clustering (SC) module. Extensive experiments on several real-world benchmarks demonstrate the effectiveness of the proposed DIAGC method compared with the state-of-the-art baselines.

Convergence Analysis of Deep Residual Networks

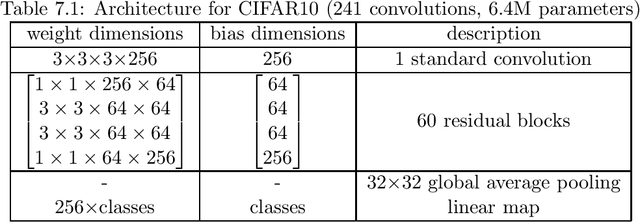
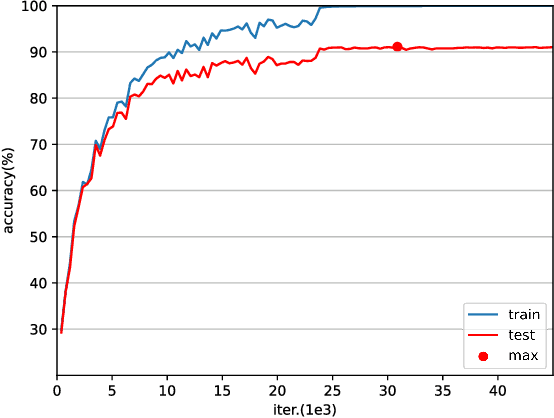
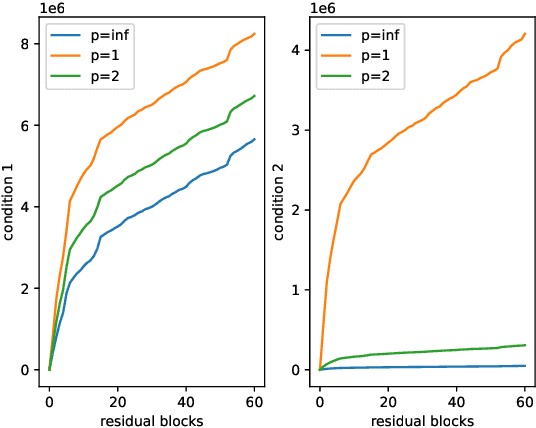
Various powerful deep neural network architectures have made great contribution to the exciting successes of deep learning in the past two decades. Among them, deep Residual Networks (ResNets) are of particular importance because they demonstrated great usefulness in computer vision by winning the first place in many deep learning competitions. Also, ResNets were the first class of neural networks in the development history of deep learning that are really deep. It is of mathematical interest and practical meaning to understand the convergence of deep ResNets. We aim at characterizing the convergence of deep ResNets as the depth tends to infinity in terms of the parameters of the networks. Toward this purpose, we first give a matrix-vector description of general deep neural networks with shortcut connections and formulate an explicit expression for the networks by using the notions of activation domains and activation matrices. The convergence is then reduced to the convergence of two series involving infinite products of non-square matrices. By studying the two series, we establish a sufficient condition for pointwise convergence of ResNets. Our result is able to give justification for the design of ResNets. We also conduct experiments on benchmark machine learning data to verify our results.

Convergence of Deep Neural Networks with General Activation Functions and Pooling

Deep neural networks, as a powerful system to represent high dimensional complex functions, play a key role in deep learning. Convergence of deep neural networks is a fundamental issue in building the mathematical foundation for deep learning. We investigated the convergence of deep ReLU networks and deep convolutional neural networks in two recent researches (arXiv:2107.12530, 2109.13542). Only the Rectified Linear Unit (ReLU) activation was studied therein, and the important pooling strategy was not considered. In this current work, we study the convergence of deep neural networks as the depth tends to infinity for two other important activation functions: the leaky ReLU and the sigmoid function. Pooling will also be studied. As a result, we prove that the sufficient condition established in arXiv:2107.12530, 2109.13542 is still sufficient for the leaky ReLU networks. For contractive activation functions such as the sigmoid function, we establish a weaker sufficient condition for uniform convergence of deep neural networks.

Convergence of Deep Convolutional Neural Networks

Convergence of deep neural networks as the depth of the networks tends to infinity is fundamental in building the mathematical foundation for deep learning. In a previous study, we investigated this question for deep ReLU networks with a fixed width. This does not cover the important convolutional neural networks where the widths are increasing from layer to layer. For this reason, we first study convergence of general ReLU networks with increasing widths and then apply the results obtained to deep convolutional neural networks. It turns out the convergence reduces to convergence of infinite products of matrices with increasing sizes, which has not been considered in the literature. We establish sufficient conditions for convergence of such infinite products of matrices. Based on the conditions, we present sufficient conditions for piecewise convergence of general deep ReLU networks with increasing widths, and as well as pointwise convergence of deep ReLU convolutional neural networks.

Convergence of Deep ReLU Networks

We explore convergence of deep neural networks with the popular ReLU activation function, as the depth of the networks tends to infinity. To this end, we introduce the notion of activation domains and activation matrices of a ReLU network. By replacing applications of the ReLU activation function by multiplications with activation matrices on activation domains, we obtain an explicit expression of the ReLU network. We then identify the convergence of the ReLU networks as convergence of a class of infinite products of matrices. Sufficient and necessary conditions for convergence of these infinite products of matrices are studied. As a result, we establish necessary conditions for ReLU networks to converge that the sequence of weight matrices converges to the identity matrix and the sequence of the bias vectors converges to zero as the depth of ReLU networks increases to infinity. Moreover, we obtain sufficient conditions in terms of the weight matrices and bias vectors at hidden layers for pointwise convergence of deep ReLU networks. These results provide mathematical insights to the design strategy of the well-known deep residual networks in image classification.

Exponential Approximation of Band-limited Signals from Nonuniform Sampling

Reconstructing a band-limited function from its finite sample data is a fundamental task in signal analysis. A simple Gaussian or hyper-Gaussian regularized Shannon sampling series has been proved to be able to achieve exponential convergence for uniform sampling. In this paper, we prove that exponential approximation can also be attained for general nonuniform sampling. The analysis is based on the the residue theorem to represent the truncated error by a contour integral. Several concrete examples of nonuniform sampling with exponential convergence will be presented.

Learning Rates for Multi-task Regularization Networks

Multi-task learning is an important trend of machine learning in facing the era of artificial intelligence and big data. Despite a large amount of researches on learning rate estimates of various single-task machine learning algorithms, there is little parallel work for multi-task learning. We present mathematical analysis on the learning rate estimate of multi-task learning based on the theory of vector-valued reproducing kernel Hilbert spaces and matrix-valued reproducing kernels. For the typical multi-task regularization networks, an explicit learning rate dependent both on the number of sample data and the number of tasks is obtained. It reveals that the generalization ability of multi-task learning algorithms is indeed affected as the number of tasks increases.

On Reproducing Kernel Banach Spaces: Generic Definitions and Unified Framework of Constructions

Recently, there has been emerging interest in constructing reproducing kernel Banach spaces (RKBS) for applied and theoretical purposes such as machine learning, sampling reconstruction, sparse approximation and functional analysis. Existing constructions include the reflexive RKBS via a bilinear form, the semi-inner-product RKBS, the RKBS with $\ell^1$ norm, the $p$-norm RKBS via generalized Mercer kernels, etc. The definitions of RKBS and the associated reproducing kernel in those references are dependent on the construction. Moreover, relations among those constructions are unclear. We explore a generic definition of RKBS and the reproducing kernel for RKBS that is independent of construction. Furthermore, we propose a framework of constructing RKBSs that unifies existing constructions mentioned above via a continuous bilinear form and a pair of feature maps. A new class of Orlicz RKBSs is proposed. Finally, we develop representer theorems for machine learning in RKBSs constructed in our framework, which also unifies representer theorems in existing RKBSs.

Universalities of Reproducing Kernels Revisited

Kernel methods have been widely applied to machine learning and other questions of approximating an unknown function from its finite sample data. To ensure arbitrary accuracy of such approximation, various denseness conditions are imposed on the selected kernel. This note contributes to the study of universal, characteristic, and $C_0$-universal kernels. We first give simple and direct description of the difference and relation among these three kinds of universalities of kernels. We then focus on translation-invariant and weighted polynomial kernels. A simple and shorter proof of the known characterization of characteristic translation-invariant kernels will be presented. The main purpose of the note is to give a delicate discussion on the universalities of weighted polynomial kernels.