Towards Quantum Tensor Decomposition in Biomedical Applications

Tensor decomposition has emerged as a powerful framework for feature extraction in multi-modal biomedical data. In this review, we present a comprehensive analysis of tensor decomposition methods such as Tucker, CANDECOMP/PARAFAC, spiked tensor decomposition, etc. and their diverse applications across biomedical domains such as imaging, multi-omics, and spatial transcriptomics. To systematically investigate the literature, we applied a topic modeling-based approach that identifies and groups distinct thematic sub-areas in biomedicine where tensor decomposition has been used, thereby revealing key trends and research directions. We evaluated challenges related to the scalability of latent spaces along with obtaining the optimal rank of the tensor, which often hinder the extraction of meaningful features from increasingly large and complex datasets. Additionally, we discuss recent advances in quantum algorithms for tensor decomposition, exploring how quantum computing can be leveraged to address these challenges. Our study includes a preliminary resource estimation analysis for quantum computing platforms and examines the feasibility of implementing quantum-enhanced tensor decomposition methods on near-term quantum devices. Collectively, this review not only synthesizes current applications and challenges of tensor decomposition in biomedical analyses but also outlines promising quantum computing strategies to enhance its impact on deriving actionable insights from complex biomedical data.

Attention is All You Need to Optimize Wind Farm Operations and Maintenance

Operations and maintenance (O&M) is a fundamental problem in wind energy systems with far reaching implications for reliability and profitability. Optimizing O&M is a multi-faceted decision optimization problem that requires a careful balancing act across turbine level failure risks, operational revenues, and maintenance crew logistics. The resulting O&M problems are typically solved using large-scale mixed integer programming (MIP) models, which yield computationally challenging problems that require either long-solution times, or heuristics to reach a solution. To address this problem, we introduce a novel decision-making framework for wind farm O&M that builds on a multi-head attention (MHA) models, an emerging artificial intelligence methods that are specifically designed to learn in rich and complex problem settings. The development of proposed MHA framework incorporates a number of modeling innovations that allows explicit embedding of MIP models within an MHA structure. The proposed MHA model (i) significantly reduces the solution time from hours to seconds, (ii) guarantees feasibility of the proposed solutions considering complex constraints that are omnipresent in wind farm O&M, (iii) results in significant solution quality compared to the conventional MIP formulations, and (iv) exhibits significant transfer learning capability across different problem settings.

Accelerating Distributed Optimization: A Primal-Dual Perspective on Local Steps

In distributed machine learning, efficient training across multiple agents with different data distributions poses significant challenges. Even with a centralized coordinator, current algorithms that achieve optimal communication complexity typically require either large minibatches or compromise on gradient complexity. In this work, we tackle both centralized and decentralized settings across strongly convex, convex, and nonconvex objectives. We first demonstrate that a basic primal-dual method, (Accelerated) Gradient Ascent Multiple Stochastic Gradient Descent (GA-MSGD), applied to the Lagrangian of distributed optimization inherently incorporates local updates, because the inner loops of running Stochastic Gradient Descent on the primal variable require no inter-agent communication. Notably, for strongly convex objectives, we show (Accelerated) GA-MSGD achieves linear convergence in communication rounds despite the Lagrangian being only linear in the dual variables. This is due to a unique structural property where the dual variable is confined to the span of the coupling matrix, rendering the dual problem strongly concave. When integrated with the Catalyst framework, our approach achieves nearly optimal communication complexity across various settings without the need for minibatches. Moreover, in stochastic decentralized problems, it attains communication complexities comparable to those in deterministic settings, improving over existing algorithms.

Federated Battery Diagnosis and Prognosis

Battery diagnosis, prognosis and health management models play a critical role in the integration of battery systems in energy and mobility fields. However, large-scale deployment of these models is hindered by a myriad of challenges centered around data ownership, privacy, communication, and processing. State-of-the-art battery diagnosis and prognosis methods require centralized collection of data, which further aggravates these challenges. Here we propose a federated battery prognosis model, which distributes the processing of battery standard current-voltage-time-usage data in a privacy-preserving manner. Instead of exchanging raw standard current-voltage-time-usage data, our model communicates only the model parameters, thus reducing communication load and preserving data confidentiality. The proposed model offers a paradigm shift in battery health management through privacy-preserving distributed methods for battery data processing and remaining lifetime prediction.

DEEP$^2$: Deep Learning Powered De-scattering with Excitation Patterning

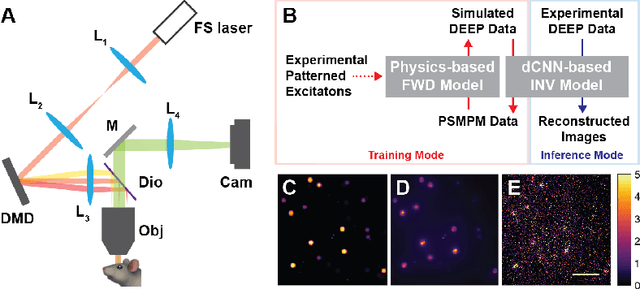
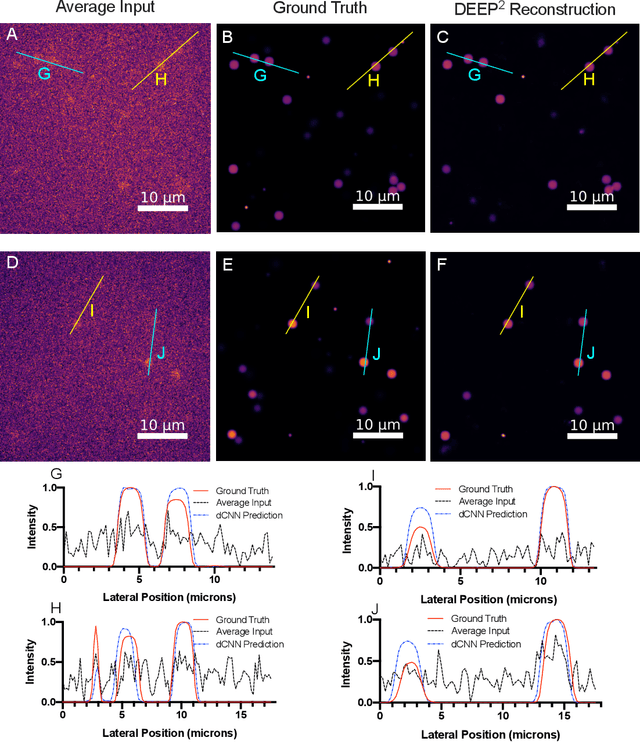
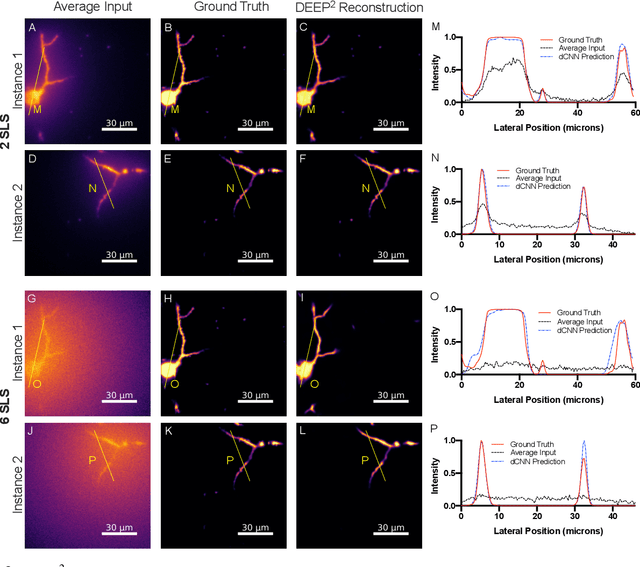
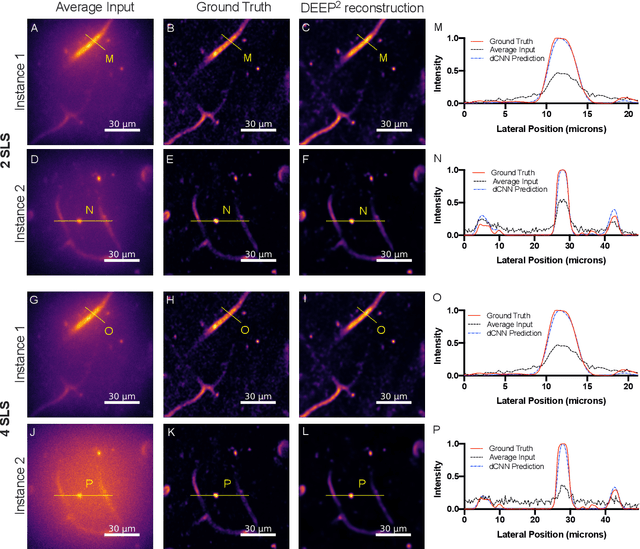
Limited throughput is a key challenge in in-vivo deep-tissue imaging using nonlinear optical microscopy. Point scanning multiphoton microscopy, the current gold standard, is slow especially compared to the wide-field imaging modalities used for optically cleared or thin specimens. We recently introduced 'De-scattering with Excitation Patterning or DEEP', as a widefield alternative to point-scanning geometries. Using patterned multiphoton excitation, DEEP encodes spatial information inside tissue before scattering. However, to de-scatter at typical depths, hundreds of such patterned excitations are needed. In this work, we present DEEP$^2$, a deep learning based model, that can de-scatter images from just tens of patterned excitations instead of hundreds. Consequently, we improve DEEP's throughput by almost an order of magnitude. We demonstrate our method in multiple numerical and physical experiments including in-vivo cortical vasculature imaging up to four scattering lengths deep, in alive mice.

Process Knowledge Driven Change Point Detection for Automated Calibration of Discrete Event Simulation Models Using Machine Learning

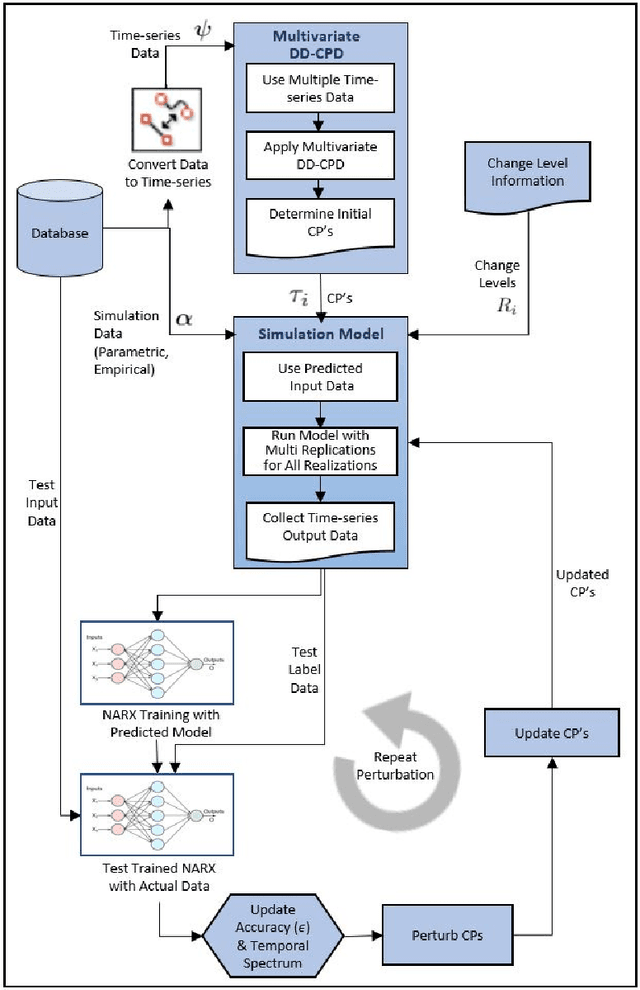
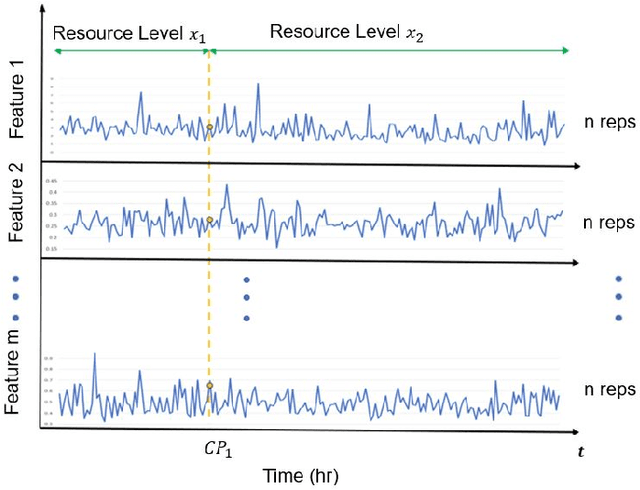
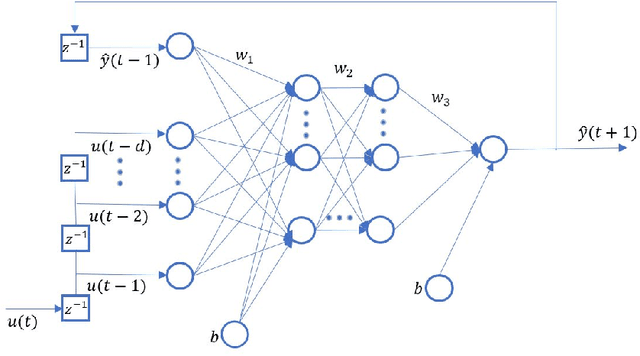
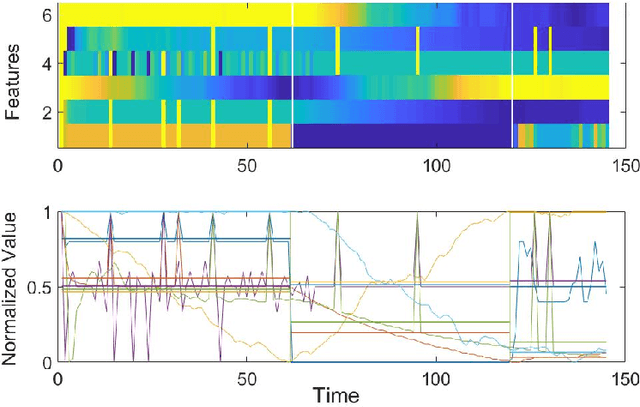
Initial development and subsequent calibration of discrete event simulation models for complex systems require accurate identification of dynamically changing process characteristics. Existing data driven change point methods (DD-CPD) assume changes are extraneous to the system, thus cannot utilize available process knowledge. This work proposes a unified framework for process-driven multi-variate change point detection (PD-CPD) by combining change point detection models with machine learning and process-driven simulation modeling. The PD-CPD, after initializing with DD-CPD's change point(s), uses simulation models to generate system level outputs as time-series data streams which are then used to train neural network models to predict system characteristics and change points. The accuracy of the predictive models measures the likelihood that the actual process data conforms to the simulated change points in system characteristics. PD-CPD iteratively optimizes change points by repeating simulation and predictive model building steps until the set of change point(s) with the maximum likelihood is identified. Using an emergency department case study, we show that PD-CPD significantly improves change point detection accuracy over DD-CPD estimates and is able to detect actual change points.