Time-Varying Graph Signal Recovery Using High-Order Smoothness and Adaptive Low-rankness
Paper and Code
May 16, 2024

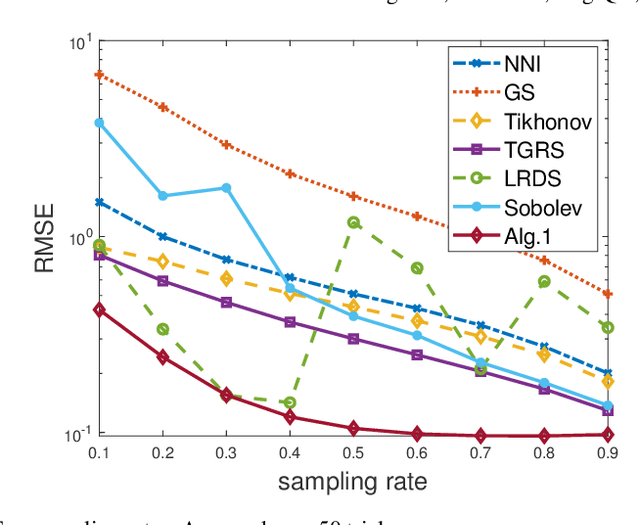
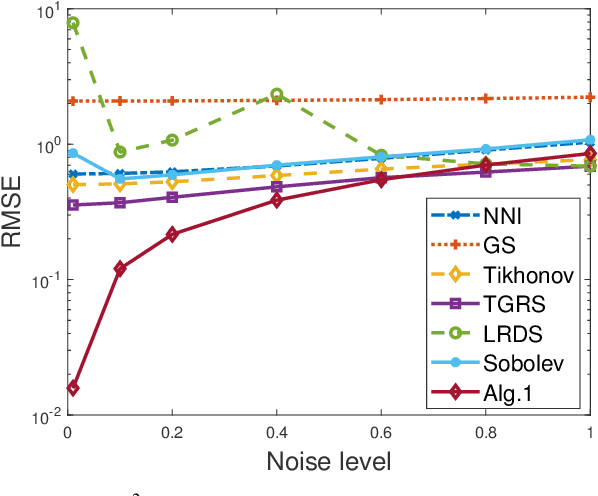
Time-varying graph signal recovery has been widely used in many applications, including climate change, environmental hazard monitoring, and epidemic studies. It is crucial to choose appropriate regularizations to describe the characteristics of the underlying signals, such as the smoothness of the signal over the graph domain and the low-rank structure of the spatial-temporal signal modeled in a matrix form. As one of the most popular options, the graph Laplacian is commonly adopted in designing graph regularizations for reconstructing signals defined on a graph from partially observed data. In this work, we propose a time-varying graph signal recovery method based on the high-order Sobolev smoothness and an error-function weighted nuclear norm regularization to enforce the low-rankness. Two efficient algorithms based on the alternating direction method of multipliers and iterative reweighting are proposed, and convergence of one algorithm is shown in detail. We conduct various numerical experiments on synthetic and real-world data sets to demonstrate the proposed method's effectiveness compared to the state-of-the-art in graph signal recovery.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge