DeepONet as a Multi-Operator Extrapolation Model: Distributed Pretraining with Physics-Informed Fine-Tuning

We propose a novel fine-tuning method to achieve multi-operator learning through training a distributed neural operator with diverse function data and then zero-shot fine-tuning the neural network using physics-informed losses for downstream tasks. Operator learning effectively approximates solution operators for PDEs and various PDE-related problems, yet it often struggles to generalize to new tasks. To address this, we investigate fine-tuning a pretrained model, while carefully selecting an initialization that enables rapid adaptation to new tasks with minimal data. Our approach combines distributed learning to integrate data from various operators in pre-training, while physics-informed methods enable zero-shot fine-tuning, minimizing the reliance on downstream data. We investigate standard fine-tuning and Low-Rank Adaptation fine-tuning, applying both to train complex nonlinear target operators that are difficult to learn only using random initialization. Through comprehensive numerical examples, we demonstrate the advantages of our approach, showcasing significant improvements in accuracy. Our findings provide a robust framework for advancing multi-operator learning and highlight the potential of transfer learning techniques in this domain.

An Energy-Based Self-Adaptive Learning Rate for Stochastic Gradient Descent: Enhancing Unconstrained Optimization with VAV method

Optimizing the learning rate remains a critical challenge in machine learning, essential for achieving model stability and efficient convergence. The Vector Auxiliary Variable (VAV) algorithm introduces a novel energy-based self-adjustable learning rate optimization method designed for unconstrained optimization problems. It incorporates an auxiliary variable $r$ to facilitate efficient energy approximation without backtracking while adhering to the unconditional energy dissipation law. Notably, VAV demonstrates superior stability with larger learning rates and achieves faster convergence in the early stage of the training process. Comparative analyses demonstrate that VAV outperforms Stochastic Gradient Descent (SGD) across various tasks. This paper also provides rigorous proof of the energy dissipation law and establishes the convergence of the algorithm under reasonable assumptions. Additionally, $r$ acts as an empirical lower bound of the training loss in practice, offering a novel scheduling approach that further enhances algorithm performance.

Conformalized Prediction of Post-Fault Voltage Trajectories Using Pre-trained and Finetuned Attention-Driven Neural Operators

This paper proposes a new data-driven methodology for predicting intervals of post-fault voltage trajectories in power systems. We begin by introducing the Quantile Attention-Fourier Deep Operator Network (QAF-DeepONet), designed to capture the complex dynamics of voltage trajectories and reliably estimate quantiles of the target trajectory without any distributional assumptions. The proposed operator regression model maps the observed portion of the voltage trajectory to its unobserved post-fault trajectory. Our methodology employs a pre-training and fine-tuning process to address the challenge of limited data availability. To ensure data privacy in learning the pre-trained model, we use merging via federated learning with data from neighboring buses, enabling the model to learn the underlying voltage dynamics from such buses without directly sharing their data. After pre-training, we fine-tune the model with data from the target bus, allowing it to adapt to unique dynamics and operating conditions. Finally, we integrate conformal prediction into the fine-tuned model to ensure coverage guarantees for the predicted intervals. We evaluated the performance of the proposed methodology using the New England 39-bus test system considering detailed models of voltage and frequency controllers. Two metrics, Prediction Interval Coverage Probability (PICP) and Prediction Interval Normalized Average Width (PINAW), are used to numerically assess the model's performance in predicting intervals. The results show that the proposed approach offers practical and reliable uncertainty quantification in predicting the interval of post-fault voltage trajectories.

Conformalized-DeepONet: A Distribution-Free Framework for Uncertainty Quantification in Deep Operator Networks

In this paper, we adopt conformal prediction, a distribution-free uncertainty quantification (UQ) framework, to obtain confidence prediction intervals with coverage guarantees for Deep Operator Network (DeepONet) regression. Initially, we enhance the uncertainty quantification frameworks (B-DeepONet and Prob-DeepONet) previously proposed by the authors by using split conformal prediction. By combining conformal prediction with our Prob- and B-DeepONets, we effectively quantify uncertainty by generating rigorous confidence intervals for DeepONet prediction. Additionally, we design a novel Quantile-DeepONet that allows for a more natural use of split conformal prediction. We refer to this distribution-free effective uncertainty quantification framework as split conformal Quantile-DeepONet regression. Finally, we demonstrate the effectiveness of the proposed methods using various ordinary, partial differential equation numerical examples, and multi-fidelity learning.

Accelerating Approximate Thompson Sampling with Underdamped Langevin Monte Carlo

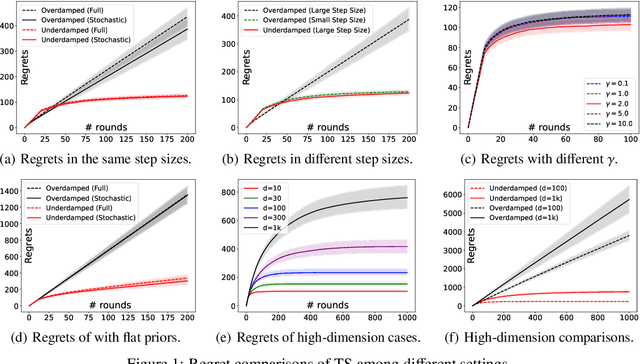
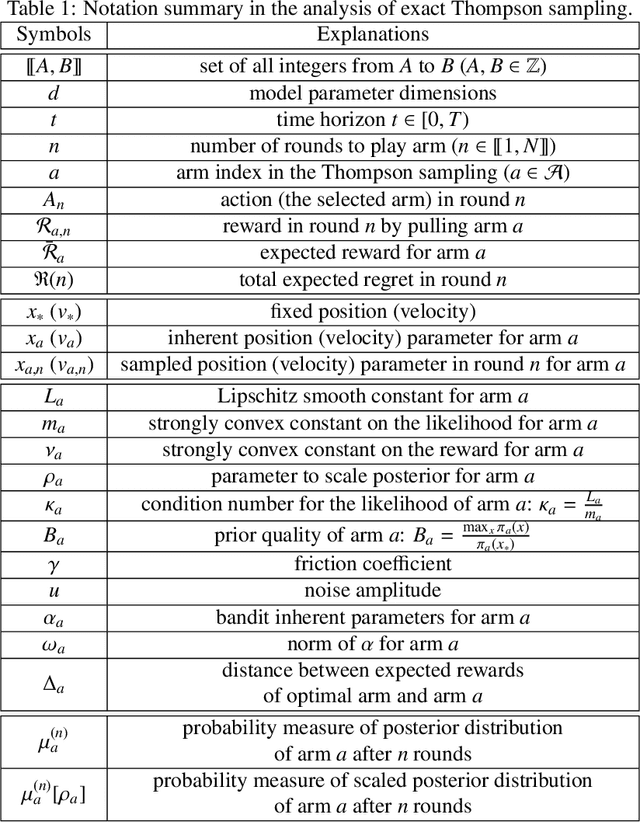
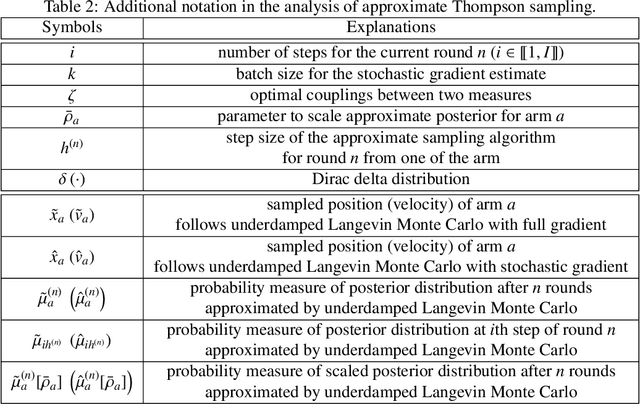
Approximate Thompson sampling with Langevin Monte Carlo broadens its reach from Gaussian posterior sampling to encompass more general smooth posteriors. However, it still encounters scalability issues in high-dimensional problems when demanding high accuracy. To address this, we propose an approximate Thompson sampling strategy, utilizing underdamped Langevin Monte Carlo, where the latter is the go-to workhorse for simulations of high-dimensional posteriors. Based on the standard smoothness and log-concavity conditions, we study the accelerated posterior concentration and sampling using a specific potential function. This design improves the sample complexity for realizing logarithmic regrets from $\mathcal{\tilde O}(d)$ to $\mathcal{\tilde O}(\sqrt{d})$. The scalability and robustness of our algorithm are also empirically validated through synthetic experiments in high-dimensional bandit problems.

B-LSTM-MIONet: Bayesian LSTM-based Neural Operators for Learning the Response of Complex Dynamical Systems to Length-Variant Multiple Input Functions

Deep Operator Network (DeepONet) is a neural network framework for learning nonlinear operators such as those from ordinary differential equations (ODEs) describing complex systems. Multiple-input deep neural operators (MIONet) extended DeepONet to allow multiple input functions in different Banach spaces. MIONet offers flexibility in training dataset grid spacing, without constraints on output location. However, it requires offline inputs and cannot handle varying sequence lengths in testing datasets, limiting its real-time application in dynamic complex systems. This work redesigns MIONet, integrating Long Short Term Memory (LSTM) to learn neural operators from time-dependent data. This approach overcomes data discretization constraints and harnesses LSTM's capability with variable-length, real-time data. Factors affecting learning performance, like algorithm extrapolation ability are presented. The framework is enhanced with uncertainty quantification through a novel Bayesian method, sampling from MIONet parameter distributions. Consequently, we develop the B-LSTM-MIONet, incorporating LSTM's temporal strengths with Bayesian robustness, resulting in a more precise and reliable model for noisy datasets.

A Physics-Guided Bi-Fidelity Fourier-Featured Operator Learning Framework for Predicting Time Evolution of Drag and Lift Coefficients

In the pursuit of accurate experimental and computational data while minimizing effort, there is a constant need for high-fidelity results. However, achieving such results often requires significant computational resources. To address this challenge, this paper proposes a deep operator learning-based framework that requires a limited high-fidelity dataset for training. We introduce a novel physics-guided, bi-fidelity, Fourier-featured Deep Operator Network (DeepONet) framework that effectively combines low and high-fidelity datasets, leveraging the strengths of each. In our methodology, we began by designing a physics-guided Fourier-featured DeepONet, drawing inspiration from the intrinsic physical behavior of the target solution. Subsequently, we train this network to primarily learn the low-fidelity solution, utilizing an extensive dataset. This process ensures a comprehensive grasp of the foundational solution patterns. Following this foundational learning, the low-fidelity deep operator network's output is enhanced using a physics-guided Fourier-featured residual deep operator network. This network refines the initial low-fidelity output, achieving the high-fidelity solution by employing a small high-fidelity dataset for training. Notably, in our framework, we employ the Fourier feature network as the Trunk network for the DeepONets, given its proficiency in capturing and learning the oscillatory nature of the target solution with high precision. We validate our approach using a well-known 2D benchmark cylinder problem, which aims to predict the time trajectories of lift and drag coefficients. The results highlight that the physics-guided Fourier-featured deep operator network, serving as a foundational building block of our framework, possesses superior predictive capability for the lift and drag coefficients compared to its data-driven counterparts.

D2NO: Efficient Handling of Heterogeneous Input Function Spaces with Distributed Deep Neural Operators

Neural operators have been applied in various scientific fields, such as solving parametric partial differential equations, dynamical systems with control, and inverse problems. However, challenges arise when dealing with input functions that exhibit heterogeneous properties, requiring multiple sensors to handle functions with minimal regularity. To address this issue, discretization-invariant neural operators have been used, allowing the sampling of diverse input functions with different sensor locations. However, existing frameworks still require an equal number of sensors for all functions. In our study, we propose a novel distributed approach to further relax the discretization requirements and solve the heterogeneous dataset challenges. Our method involves partitioning the input function space and processing individual input functions using independent and separate neural networks. A centralized neural network is used to handle shared information across all output functions. This distributed methodology reduces the number of gradient descent back-propagation steps, improving efficiency while maintaining accuracy. We demonstrate that the corresponding neural network is a universal approximator of continuous nonlinear operators and present four numerical examples to validate its performance.

Deep Operator Learning-based Surrogate Models with Uncertainty Quantification for Optimizing Internal Cooling Channel Rib Profiles

This paper designs surrogate models with uncertainty quantification capabilities to improve the thermal performance of rib-turbulated internal cooling channels effectively. To construct the surrogate, we use the deep operator network (DeepONet) framework, a novel class of neural networks designed to approximate mappings between infinite-dimensional spaces using relatively small datasets. The proposed DeepONet takes an arbitrary continuous rib geometry with control points as input and outputs continuous detailed information about the distribution of pressure and heat transfer around the profiled ribs. The datasets needed to train and test the proposed DeepONet framework were obtained by simulating a 2D rib-roughened internal cooling channel. To accomplish this, we continuously modified the input rib geometry by adjusting the control points according to a simple random distribution with constraints, rather than following a predefined path or sampling method. The studied channel has a hydraulic diameter, Dh, of 66.7 mm, and a length-to-hydraulic diameter ratio, L/Dh, of 10. The ratio of rib center height to hydraulic diameter (e/Dh), which was not changed during the rib profile update, was maintained at a constant value of 0.048. The ribs were placed in the channel with a pitch-to-height ratio (P/e) of 10. In addition, we provide the proposed surrogates with effective uncertainty quantification capabilities. This is achieved by converting the DeepONet framework into a Bayesian DeepONet (B-DeepONet). B-DeepONet samples from the posterior distribution of DeepONet parameters using the novel framework of stochastic gradient replica-exchange MCMC.

On Approximating the Dynamic Response of Synchronous Generators via Operator Learning: A Step Towards Building Deep Operator-based Power Grid Simulators

This paper designs an Operator Learning framework to approximate the dynamic response of synchronous generators. One can use such a framework to (i) design a neural-based generator model that can interact with a numerical simulator of the rest of the power grid or (ii) shadow the generator's transient response. To this end, we design a data-driven Deep Operator Network~(DeepONet) that approximates the generators' infinite-dimensional solution operator. Then, we develop a DeepONet-based numerical scheme to simulate a given generator's dynamic response over a short/medium-term horizon. The proposed numerical scheme recursively employs the trained DeepONet to simulate the response for a given multi-dimensional input, which describes the interaction between the generator and the rest of the system. Furthermore, we develop a residual DeepONet numerical scheme that incorporates information from mathematical models of synchronous generators. We accompany this residual DeepONet scheme with an estimate for the prediction's cumulative error. We also design a data aggregation (DAgger) strategy that allows (i) employing supervised learning to train the proposed DeepONets and (ii) fine-tuning the DeepONet using aggregated training data that the DeepONet is likely to encounter during interactive simulations with other grid components. Finally, as a proof of concept, we demonstrate that the proposed DeepONet frameworks can effectively approximate the transient model of a synchronous generator.