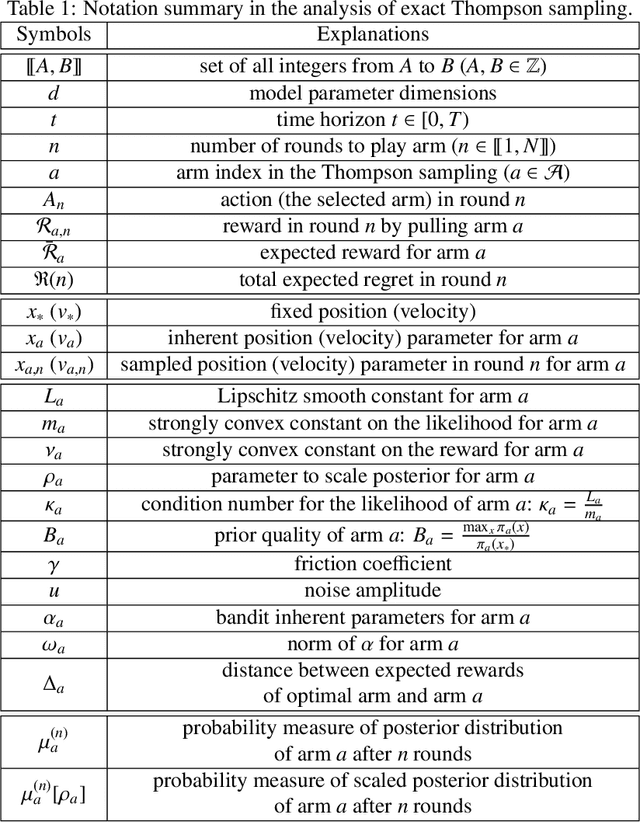
Haoyang Zheng
Rethinking Langevin Thompson Sampling from A Stochastic Approximation Perspective
Oct 06, 2025Abstract:Most existing approximate Thompson Sampling (TS) algorithms for multi-armed bandits use Stochastic Gradient Langevin Dynamics (SGLD) or its variants in each round to sample from the posterior, relaxing the need for conjugacy assumptions between priors and reward distributions in vanilla TS. However, they often require approximating a different posterior distribution in different round of the bandit problem. This requires tricky, round-specific tuning of hyperparameters such as dynamic learning rates, causing challenges in both theoretical analysis and practical implementation. To alleviate this non-stationarity, we introduce TS-SA, which incorporates stochastic approximation (SA) within the TS framework. In each round, TS-SA constructs a posterior approximation only using the most recent reward(s), performs a Langevin Monte Carlo (LMC) update, and applies an SA step to average noisy proposals over time. This can be interpreted as approximating a stationary posterior target throughout the entire algorithm, which further yields a fixed step-size, a unified convergence analysis framework, and improved posterior estimates through temporal averaging. We establish near-optimal regret bounds for TS-SA, with a simplified and more intuitive theoretical analysis enabled by interpreting the entire algorithm as a simulation of a stationary SGLD process. Our empirical results demonstrate that even a single-step Langevin update with certain warm-up outperforms existing methods substantially on bandit tasks.
Skeleton-based sign language recognition using a dual-stream spatio-temporal dynamic graph convolutional network
Sep 10, 2025Abstract:Isolated Sign Language Recognition (ISLR) is challenged by gestures that are morphologically similar yet semantically distinct, a problem rooted in the complex interplay between hand shape and motion trajectory. Existing methods, often relying on a single reference frame, struggle to resolve this geometric ambiguity. This paper introduces Dual-SignLanguageNet (DSLNet), a dual-reference, dual-stream architecture that decouples and models gesture morphology and trajectory in separate, complementary coordinate systems. Our approach utilizes a wrist-centric frame for view-invariant shape analysis and a facial-centric frame for context-aware trajectory modeling. These streams are processed by specialized networks-a topology-aware graph convolution for shape and a Finsler geometry-based encoder for trajectory-and are integrated via a geometry-driven optimal transport fusion mechanism. DSLNet sets a new state-of-the-art, achieving 93.70%, 89.97% and 99.79% accuracy on the challenging WLASL-100, WLASL-300 and LSA64 datasets, respectively, with significantly fewer parameters than competing models.
Self-Supervised Continuous Colormap Recovery from a 2D Scalar Field Visualization without a Legend
Jul 28, 2025Abstract:Recovering a continuous colormap from a single 2D scalar field visualization can be quite challenging, especially in the absence of a corresponding color legend. In this paper, we propose a novel colormap recovery approach that extracts the colormap from a color-encoded 2D scalar field visualization by simultaneously predicting the colormap and underlying data using a decoupling-and-reconstruction strategy. Our approach first separates the input visualization into colormap and data using a decoupling module, then reconstructs the visualization with a differentiable color-mapping module. To guide this process, we design a reconstruction loss between the input and reconstructed visualizations, which serves both as a constraint to ensure strong correlation between colormap and data during training, and as a self-supervised optimizer for fine-tuning the predicted colormap of unseen visualizations during inferencing. To ensure smoothness and correct color ordering in the extracted colormap, we introduce a compact colormap representation using cubic B-spline curves and an associated color order loss. We evaluate our method quantitatively and qualitatively on a synthetic dataset and a collection of real-world visualizations from the VIS30K dataset. Additionally, we demonstrate its utility in two prototype applications -- colormap adjustment and colormap transfer -- and explore its generalization to visualizations with color legends and ones encoded using discrete color palettes.
LAPD: Langevin-Assisted Bayesian Active Learning for Physical Discovery
Mar 04, 2025Abstract:Discovering physical laws from data is a fundamental challenge in scientific research, particularly when high-quality data are scarce or costly to obtain. Traditional methods for identifying dynamical systems often struggle with noise sensitivity, inefficiency in data usage, and the inability to quantify uncertainty effectively. To address these challenges, we propose Langevin-Assisted Active Physical Discovery (LAPD), a Bayesian framework that integrates replica-exchange stochastic gradient Langevin Monte Carlo to simultaneously enable efficient system identification and robust uncertainty quantification (UQ). By balancing gradient-driven exploration in coefficient space and generating an ensemble of candidate models during exploitation, LAPD achieves reliable, uncertainty-aware identification with noisy data. In the face of data scarcity, the probabilistic foundation of LAPD further promotes the integration of active learning (AL) via a hybrid uncertainty-space-filling acquisition function. This strategy sequentially selects informative data to reduce data collection costs while maintaining accuracy. We evaluate LAPD on diverse nonlinear systems such as the Lotka-Volterra, Lorenz, Burgers, and Convection-Diffusion equations, demonstrating its robustness with noisy and limited data as well as superior uncertainty calibration compared to existing methods. The AL extension reduces the required measurements by around 60% for the Lotka-Volterra system and by around 40% for Burgers' equation compared to random data sampling, highlighting its potential for resource-constrained experiments. Our framework establishes a scalable, uncertainty-aware methodology for data-efficient discovery of dynamical systems, with broad applicability to problems where high-fidelity data acquisition is prohibitively expensive.
Exploring Non-Convex Discrete Energy Landscapes: A Langevin-Like Sampler with Replica Exchange
Jan 28, 2025Abstract:Gradient-based Discrete Samplers (GDSs) are effective for sampling discrete energy landscapes. However, they often stagnate in complex, non-convex settings. To improve exploration, we introduce the Discrete Replica EXchangE Langevin (DREXEL) sampler and its variant with Adjusted Metropolis (DREAM). These samplers use two GDSs at different temperatures and step sizes: one focuses on local exploitation, while the other explores broader energy landscapes. When energy differences are significant, sample swaps occur, which are determined by a mechanism tailored for discrete sampling to ensure detailed balance. Theoretically, we prove both DREXEL and DREAM converge asymptotically to the target energy and exhibit faster mixing than a single GDS. Experiments further confirm their efficiency in exploring non-convex discrete energy landscapes.
LES-SINDy: Laplace-Enhanced Sparse Identification of Nonlinear Dynamical Systems
Nov 04, 2024Abstract:Sparse Identification of Nonlinear Dynamical Systems (SINDy) is a powerful tool for the data-driven discovery of governing equations. However, it encounters challenges when modeling complex dynamical systems involving high-order derivatives or discontinuities, particularly in the presence of noise. These limitations restrict its applicability across various fields in applied mathematics and physics. To mitigate these, we propose Laplace-Enhanced SparSe Identification of Nonlinear Dynamical Systems (LES-SINDy). By transforming time-series measurements from the time domain to the Laplace domain using the Laplace transform and integration by parts, LES-SINDy enables more accurate approximations of derivatives and discontinuous terms. It also effectively handles unbounded growth functions and accumulated numerical errors in the Laplace domain, thereby overcoming challenges in the identification process. The model evaluation process selects the most accurate and parsimonious dynamical systems from multiple candidates. Experimental results across diverse ordinary and partial differential equations show that LES-SINDy achieves superior robustness, accuracy, and parsimony compared to existing methods.
Constrained Exploration via Reflected Replica Exchange Stochastic Gradient Langevin Dynamics
May 13, 2024



Abstract:Replica exchange stochastic gradient Langevin dynamics (reSGLD) is an effective sampler for non-convex learning in large-scale datasets. However, the simulation may encounter stagnation issues when the high-temperature chain delves too deeply into the distribution tails. To tackle this issue, we propose reflected reSGLD (r2SGLD): an algorithm tailored for constrained non-convex exploration by utilizing reflection steps within a bounded domain. Theoretically, we observe that reducing the diameter of the domain enhances mixing rates, exhibiting a \emph{quadratic} behavior. Empirically, we test its performance through extensive experiments, including identifying dynamical systems with physical constraints, simulations of constrained multi-modal distributions, and image classification tasks. The theoretical and empirical findings highlight the crucial role of constrained exploration in improving the simulation efficiency.
Accelerating Approximate Thompson Sampling with Underdamped Langevin Monte Carlo
Jan 22, 2024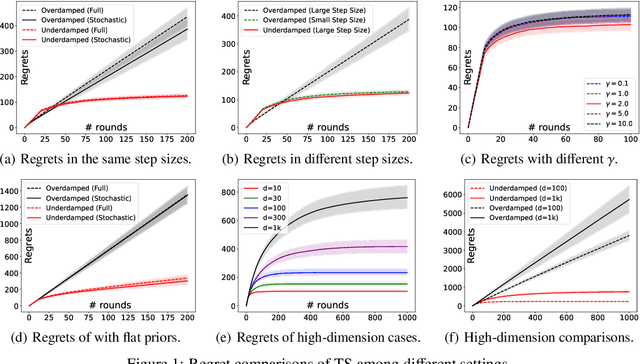
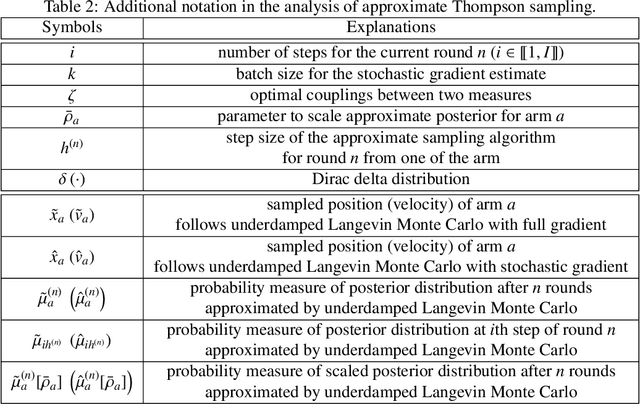

Abstract:Approximate Thompson sampling with Langevin Monte Carlo broadens its reach from Gaussian posterior sampling to encompass more general smooth posteriors. However, it still encounters scalability issues in high-dimensional problems when demanding high accuracy. To address this, we propose an approximate Thompson sampling strategy, utilizing underdamped Langevin Monte Carlo, where the latter is the go-to workhorse for simulations of high-dimensional posteriors. Based on the standard smoothness and log-concavity conditions, we study the accelerated posterior concentration and sampling using a specific potential function. This design improves the sample complexity for realizing logarithmic regrets from $\mathcal{\tilde O}(d)$ to $\mathcal{\tilde O}(\sqrt{d})$. The scalability and robustness of our algorithm are also empirically validated through synthetic experiments in high-dimensional bandit problems.
HomPINNs: homotopy physics-informed neural networks for solving the inverse problems of nonlinear differential equations with multiple solutions
Apr 06, 2023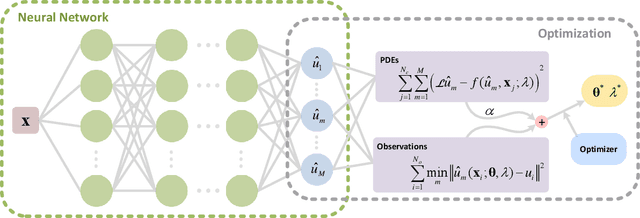
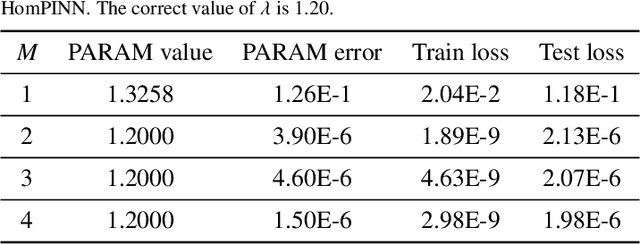
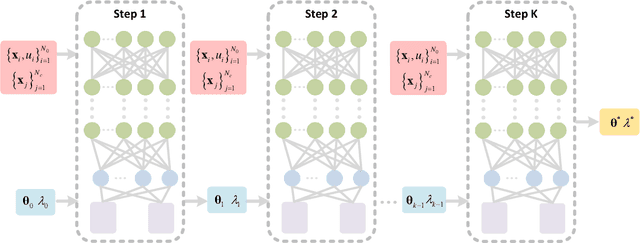
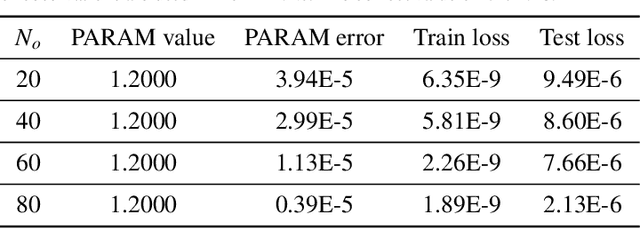
Abstract:Due to the complex behavior arising from non-uniqueness, symmetry, and bifurcations in the solution space, solving inverse problems of nonlinear differential equations (DEs) with multiple solutions is a challenging task. To address this issue, we propose homotopy physics-informed neural networks (HomPINNs), a novel framework that leverages homotopy continuation and neural networks (NNs) to solve inverse problems. The proposed framework begins with the use of a NN to simultaneously approximate known observations and conform to the constraints of DEs. By utilizing the homotopy continuation method, the approximation traces the observations to identify multiple solutions and solve the inverse problem. The experiments involve testing the performance of the proposed method on one-dimensional DEs and applying it to solve a two-dimensional Gray-Scott simulation. Our findings demonstrate that the proposed method is scalable and adaptable, providing an effective solution for solving DEs with multiple solutions and unknown parameters. Moreover, it has significant potential for various applications in scientific computing, such as modeling complex systems and solving inverse problems in physics, chemistry, biology, etc.
PCNN: A physics-constrained neural network for multiphase flows
Sep 18, 2021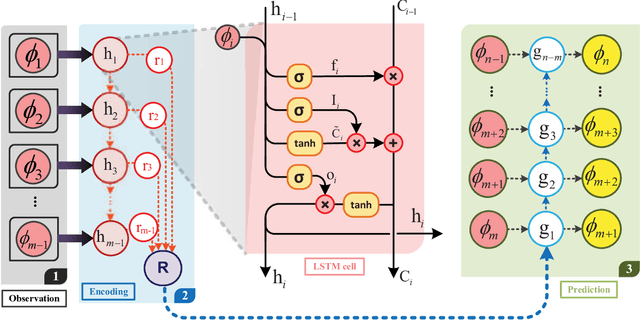
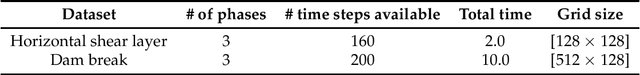
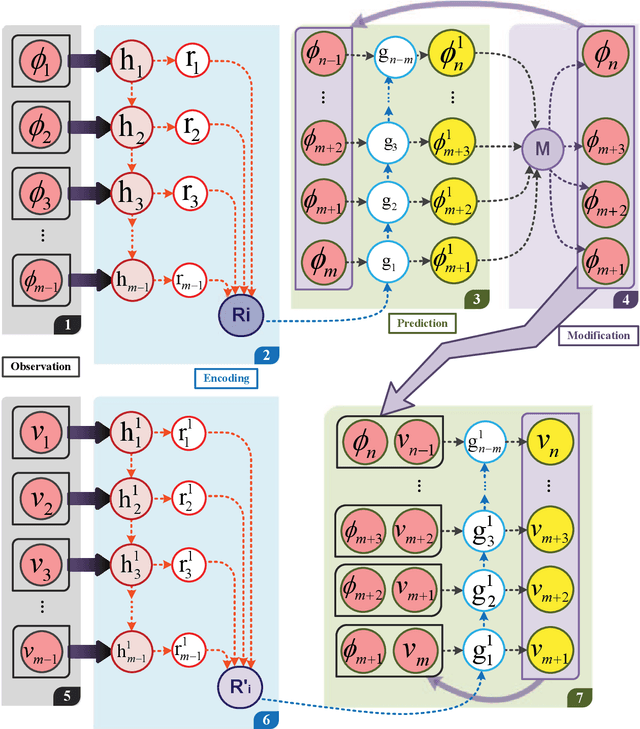
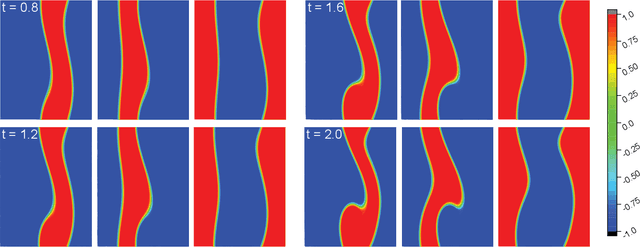
Abstract:The present study develops a physics-constrained neural network (PCNN) to predict sequential patterns and motions of multiphase flows (MPFs), which includes strong interactions among various fluid phases. To predict the order parameters, which locate individual phases, in the future time, the conditional neural processes and long short-term memory (CNP-LSTM) are applied to quickly infer the dynamics of the phases after encoding only a few observations. After that, the multiphase consistent and conservative boundedness mapping algorithm (MCBOM) is implemented to correct the order parameters predicted from CNP-LSTM in order to strictly satisfy the mass conservation, the summation of the volume fractions of the phases to be unity, the consistency of reduction, and the boundedness of the order parameters. Then, the density of the fluid mixture is updated from the corrected order parameters. Finally, the velocity in the future time is predicted by a physics-informed CNP-LSTM (PICNP-LSTM) where conservation of momentum is included in the loss function with the observed density and velocity as the inputs. The proposed PCNN for MPFs sequentially performs (CNP-LSTM)-(MCBOM)-(PICNP-LSTM), which avoids unphysical behaviors of the order parameters, accelerates the convergence, and requires fewer data to make predictions. Numerical experiments demonstrate that the proposed PCNN is capable of predicting MPFs effectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge