HomPINNs: homotopy physics-informed neural networks for solving the inverse problems of nonlinear differential equations with multiple solutions
Paper and Code
Apr 06, 2023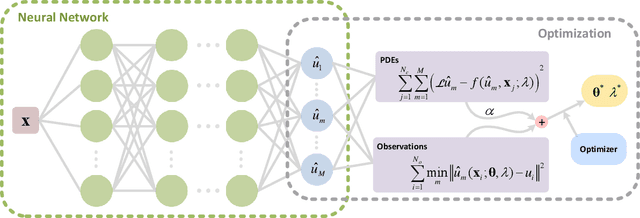
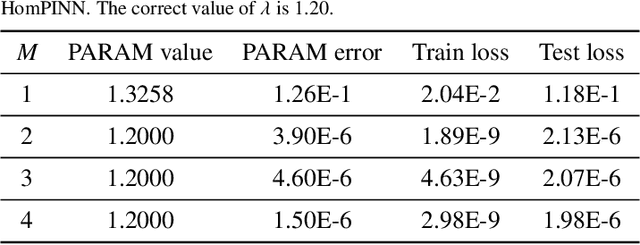
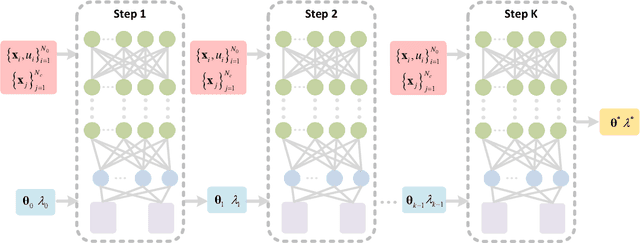
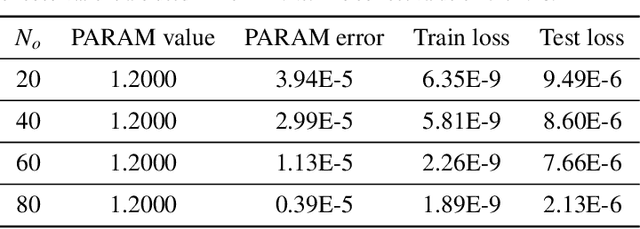
Due to the complex behavior arising from non-uniqueness, symmetry, and bifurcations in the solution space, solving inverse problems of nonlinear differential equations (DEs) with multiple solutions is a challenging task. To address this issue, we propose homotopy physics-informed neural networks (HomPINNs), a novel framework that leverages homotopy continuation and neural networks (NNs) to solve inverse problems. The proposed framework begins with the use of a NN to simultaneously approximate known observations and conform to the constraints of DEs. By utilizing the homotopy continuation method, the approximation traces the observations to identify multiple solutions and solve the inverse problem. The experiments involve testing the performance of the proposed method on one-dimensional DEs and applying it to solve a two-dimensional Gray-Scott simulation. Our findings demonstrate that the proposed method is scalable and adaptable, providing an effective solution for solving DEs with multiple solutions and unknown parameters. Moreover, it has significant potential for various applications in scientific computing, such as modeling complex systems and solving inverse problems in physics, chemistry, biology, etc.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge