Greedy Output Approximation: Towards Efficient Structured Pruning for LLMs Without Retraining

To remove redundant components of large language models (LLMs) without incurring significant computational costs, this work focuses on single-shot pruning without a retraining phase. We simplify the pruning process for Transformer-based LLMs by identifying a depth-2 pruning structure that functions independently. Additionally, we propose two inference-aware pruning criteria derived from the optimization perspective of output approximation, which outperforms traditional training-aware metrics such as gradient and Hessian. We also introduce a two-step reconstruction technique to mitigate pruning errors without model retraining. Experimental results demonstrate that our approach significantly reduces computational costs and hardware requirements while maintaining superior performance across various datasets and models.

Sketchy Moment Matching: Toward Fast and Provable Data Selection for Finetuning

We revisit data selection in a modern context of finetuning from a fundamental perspective. Extending the classical wisdom of variance minimization in low dimensions to high-dimensional finetuning, our generalization analysis unveils the importance of additionally reducing bias induced by low-rank approximation. Inspired by the variance-bias tradeoff in high dimensions from the theory, we introduce Sketchy Moment Matching (SkMM), a scalable data selection scheme with two stages. (i) First, the bias is controlled using gradient sketching that explores the finetuning parameter space for an informative low-dimensional subspace $\mathcal{S}$; (ii) then the variance is reduced over $\mathcal{S}$ via moment matching between the original and selected datasets. Theoretically, we show that gradient sketching is fast and provably accurate: selecting $n$ samples by reducing variance over $\mathcal{S}$ preserves the fast-rate generalization $O(\dim(\mathcal{S})/n)$, independent of the parameter dimension. Empirically, we concretize the variance-bias balance via synthetic experiments and demonstrate the effectiveness of SkMM for finetuning in real vision tasks.

Randomized Dimension Reduction with Statistical Guarantees

Large models and enormous data are essential driving forces of the unprecedented successes achieved by modern algorithms, especially in scientific computing and machine learning. Nevertheless, the growing dimensionality and model complexity, as well as the non-negligible workload of data pre-processing, also bring formidable costs to such successes in both computation and data aggregation. As the deceleration of Moore's Law slackens the cost reduction of computation from the hardware level, fast heuristics for expensive classical routines and efficient algorithms for exploiting limited data are increasingly indispensable for pushing the limit of algorithm potency. This thesis explores some of such algorithms for fast execution and efficient data utilization. From the computational efficiency perspective, we design and analyze fast randomized low-rank decomposition algorithms for large matrices based on "matrix sketching", which can be regarded as a dimension reduction strategy in the data space. These include the randomized pivoting-based interpolative and CUR decomposition discussed in Chapter 2 and the randomized subspace approximations discussed in Chapter 3. From the sample efficiency perspective, we focus on learning algorithms with various incorporations of data augmentation that improve generalization and distributional robustness provably. Specifically, Chapter 4 presents a sample complexity analysis for data augmentation consistency regularization where we view sample efficiency from the lens of dimension reduction in the function space. Then in Chapter 5, we introduce an adaptively weighted data augmentation consistency regularization algorithm for distributionally robust optimization with applications in medical image segmentation.

Cluster-aware Semi-supervised Learning: Relational Knowledge Distillation Provably Learns Clustering

Despite the empirical success and practical significance of (relational) knowledge distillation that matches (the relations of) features between teacher and student models, the corresponding theoretical interpretations remain limited for various knowledge distillation paradigms. In this work, we take an initial step toward a theoretical understanding of relational knowledge distillation (RKD), with a focus on semi-supervised classification problems. We start by casting RKD as spectral clustering on a population-induced graph unveiled by a teacher model. Via a notion of clustering error that quantifies the discrepancy between the predicted and ground truth clusterings, we illustrate that RKD over the population provably leads to low clustering error. Moreover, we provide a sample complexity bound for RKD with limited unlabeled samples. For semi-supervised learning, we further demonstrate the label efficiency of RKD through a general framework of cluster-aware semi-supervised learning that assumes low clustering errors. Finally, by unifying data augmentation consistency regularization into this cluster-aware framework, we show that despite the common effect of learning accurate clusterings, RKD facilitates a "global" perspective through spectral clustering, whereas consistency regularization focuses on a "local" perspective via expansion.

AdaWAC: Adaptively Weighted Augmentation Consistency Regularization for Volumetric Medical Image Segmentation

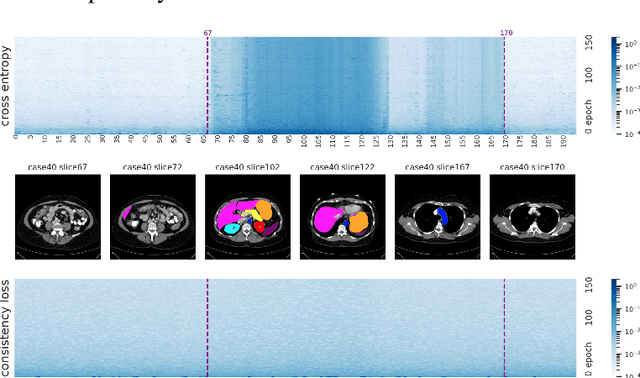
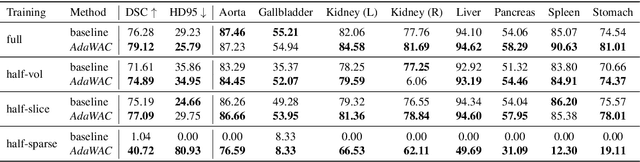
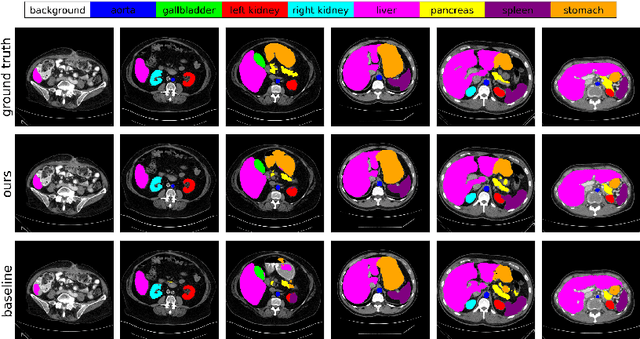
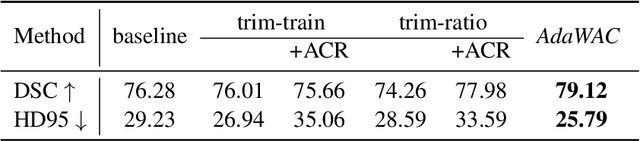
Sample reweighting is an effective strategy for learning from training data coming from a mixture of subpopulations. In volumetric medical image segmentation, the data inputs are similarly distributed, but the associated data labels fall into two subpopulations -- "label-sparse" and "label-dense" -- depending on whether the data image occurs near the beginning/end of the volumetric scan or the middle. Existing reweighting algorithms have focused on hard- and soft- thresholding of the label-sparse data, which results in loss of information and reduced sample efficiency by discarding valuable data input. For this setting, we propose AdaWAC as an adaptive weighting algorithm that introduces a set of trainable weights which, at the saddle point of the underlying objective, assigns label-dense samples to supervised cross-entropy loss and label-sparse samples to unsupervised consistency regularization. We provide a convergence guarantee for AdaWAC by recasting the optimization as online mirror descent on a saddle point problem. Moreover, we empirically demonstrate that AdaWAC not only enhances segmentation performance and sample efficiency but also improves robustness to the subpopulation shift in labels.

Sample Efficiency of Data Augmentation Consistency Regularization

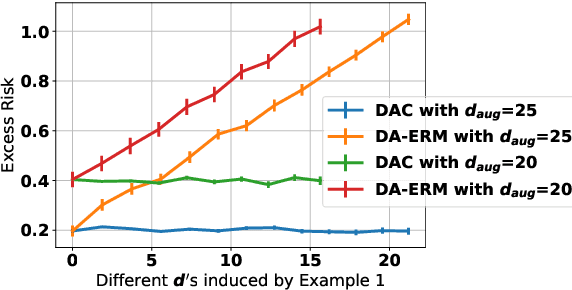
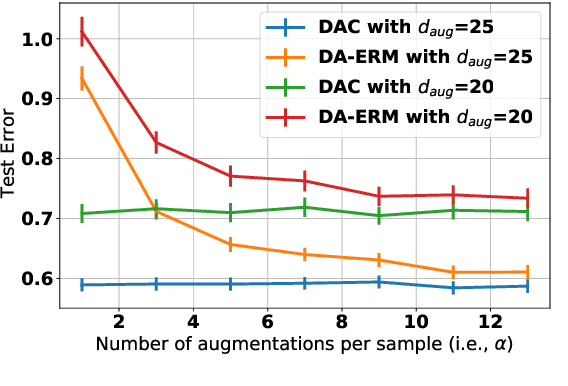
Data augmentation is popular in the training of large neural networks; currently, however, there is no clear theoretical comparison between different algorithmic choices on how to use augmented data. In this paper, we take a step in this direction - we first present a simple and novel analysis for linear regression, demonstrating that data augmentation consistency (DAC) is intrinsically more efficient than empirical risk minimization on augmented data (DA-ERM). We then propose a new theoretical framework for analyzing DAC, which reframes DAC as a way to reduce function class complexity. The new framework characterizes the sample efficiency of DAC for various non-linear models (e.g., neural networks). Further, we perform experiments that make a clean and apples-to-apples comparison (i.e., with no extra modeling or data tweaks) between ERM and consistency regularization using CIFAR-100 and WideResNet; these together demonstrate the superior efficacy of DAC.