Sample Efficiency of Data Augmentation Consistency Regularization
Paper and Code
Feb 24, 2022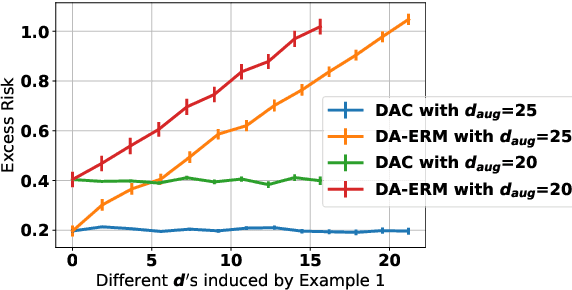

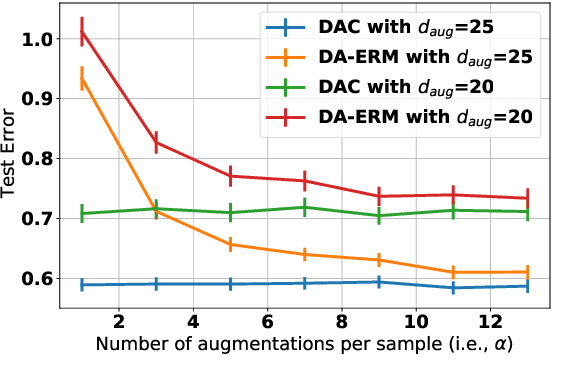

Data augmentation is popular in the training of large neural networks; currently, however, there is no clear theoretical comparison between different algorithmic choices on how to use augmented data. In this paper, we take a step in this direction - we first present a simple and novel analysis for linear regression, demonstrating that data augmentation consistency (DAC) is intrinsically more efficient than empirical risk minimization on augmented data (DA-ERM). We then propose a new theoretical framework for analyzing DAC, which reframes DAC as a way to reduce function class complexity. The new framework characterizes the sample efficiency of DAC for various non-linear models (e.g., neural networks). Further, we perform experiments that make a clean and apples-to-apples comparison (i.e., with no extra modeling or data tweaks) between ERM and consistency regularization using CIFAR-100 and WideResNet; these together demonstrate the superior efficacy of DAC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge