Yicheng Li
InstructAttribute: Fine-grained Object Attributes editing with Instruction
May 01, 2025Abstract:Text-to-image (T2I) diffusion models, renowned for their advanced generative abilities, are extensively utilized in image editing applications, demonstrating remarkable effectiveness. However, achieving precise control over fine-grained attributes still presents considerable challenges. Existing image editing techniques either fail to modify the attributes of an object or struggle to preserve its structure and maintain consistency in other areas of the image. To address these challenges, we propose the Structure-Preserving and Attribute Amplification (SPAA), a training-free method which enables precise control over the color and material transformations of objects by editing the self-attention maps and cross-attention values. Furthermore, we constructed the Attribute Dataset, which encompasses nearly all colors and materials associated with various objects, by integrating multimodal large language models (MLLM) to develop an automated pipeline for data filtering and instruction labeling. Training on this dataset, we present our InstructAttribute, an instruction-based model designed to facilitate fine-grained editing of color and material attributes. Extensive experiments demonstrate that our method achieves superior performance in object-level color and material editing, outperforming existing instruction-based image editing approaches.
Euclidean Distance Matrix Completion via Asymmetric Projected Gradient Descent
Apr 28, 2025Abstract:This paper proposes and analyzes a gradient-type algorithm based on Burer-Monteiro factorization, called the Asymmetric Projected Gradient Descent (APGD), for reconstructing the point set configuration from partial Euclidean distance measurements, known as the Euclidean Distance Matrix Completion (EDMC) problem. By paralleling the incoherence matrix completion framework, we show for the first time that global convergence guarantee with exact recovery of this routine can be established given $\mathcal{O}(\mu^2 r^3 \kappa^2 n \log n)$ Bernoulli random observations without any sample splitting. Unlike leveraging the tangent space Restricted Isometry Property (RIP) and local curvature of the low-rank embedding manifold in some very recent works, our proof provides new upper bounds to replace the random graph lemma under EDMC setting. The APGD works surprisingly well and numerical experiments demonstrate exact linear convergence behavior in rich-sample regions yet deteriorates fast when compared with the performance obtained by optimizing the s-stress function, i.e., the standard but unexplained non-convex approach for EDMC, if the sample size is limited. While virtually matching our theoretical prediction, this unusual phenomenon might indicate that: (i) the power of implicit regularization is weakened when specified in the APGD case; (ii) the stabilization of such new gradient direction requires substantially more samples than the information-theoretic limit would suggest.
TimeChat-Online: 80% Visual Tokens are Naturally Redundant in Streaming Videos
Apr 24, 2025Abstract:The rapid growth of online video platforms, particularly live streaming services, has created an urgent need for real-time video understanding systems. These systems must process continuous video streams and respond to user queries instantaneously, presenting unique challenges for current Video Large Language Models (VideoLLMs). While existing VideoLLMs excel at processing complete videos, they face significant limitations in streaming scenarios due to their inability to handle dense, redundant frames efficiently. We introduce TimeChat-Online, a novel online VideoLLM that revolutionizes real-time video interaction. At its core lies our innovative Differential Token Drop (DTD) module, which addresses the fundamental challenge of visual redundancy in streaming videos. Drawing inspiration from human visual perception's Change Blindness phenomenon, DTD preserves meaningful temporal changes while filtering out static, redundant content between frames. Remarkably, our experiments demonstrate that DTD achieves an 82.8% reduction in video tokens while maintaining 98% performance on StreamingBench, revealing that over 80% of visual content in streaming videos is naturally redundant without requiring language guidance. To enable seamless real-time interaction, we present TimeChat-Online-139K, a comprehensive streaming video dataset featuring diverse interaction patterns including backward-tracing, current-perception, and future-responding scenarios. TimeChat-Online's unique Proactive Response capability, naturally achieved through continuous monitoring of video scene transitions via DTD, sets it apart from conventional approaches. Our extensive evaluation demonstrates TimeChat-Online's superior performance on streaming benchmarks (StreamingBench and OvOBench) and maintaining competitive results on long-form video tasks such as Video-MME and MLVU.
Neural Tangent Kernel of Neural Networks with Loss Informed by Differential Operators
Mar 14, 2025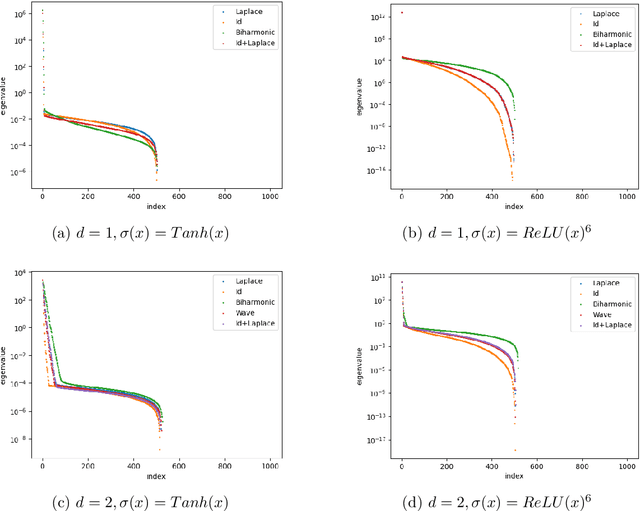

Abstract:Spectral bias is a significant phenomenon in neural network training and can be explained by neural tangent kernel (NTK) theory. In this work, we develop the NTK theory for deep neural networks with physics-informed loss, providing insights into the convergence of NTK during initialization and training, and revealing its explicit structure. We find that, in most cases, the differential operators in the loss function do not induce a faster eigenvalue decay rate and stronger spectral bias. Some experimental results are also presented to verify the theory.
Discrepancies are Virtue: Weak-to-Strong Generalization through Lens of Intrinsic Dimension
Feb 07, 2025



Abstract:Weak-to-strong (W2S) generalization is a type of finetuning (FT) where a strong (large) student model is trained on pseudo-labels generated by a weak teacher. Surprisingly, W2S FT often outperforms the weak teacher. We seek to understand this phenomenon through the observation that FT often occurs in intrinsically low-dimensional spaces. Leveraging the low intrinsic dimensionality of FT, we analyze W2S in the ridgeless regression setting from a variance reduction perspective. For a strong student - weak teacher pair with sufficiently expressive low-dimensional feature subspaces $\mathcal{V}_s, \mathcal{V}_w$, we provide an exact characterization of the variance that dominates the generalization error of W2S. This unveils a virtue of discrepancy between the strong and weak models in W2S: the variance of the weak teacher is inherited by the strong student in $\mathcal{V}_s \cap \mathcal{V}_w$, while reduced by a factor of $\dim(\mathcal{V}_s)/N$ in the subspace of discrepancy $\mathcal{V}_w \setminus \mathcal{V}_s$ with $N$ pseudo-labels for W2S. Further, our analysis casts light on the sample complexities and the scaling of performance gap recovery in W2S. The analysis is supported with experiments on both synthetic regression problems and real vision tasks.
Diagonal Over-parameterization in Reproducing Kernel Hilbert Spaces as an Adaptive Feature Model: Generalization and Adaptivity
Jan 15, 2025

Abstract:This paper introduces a diagonal adaptive kernel model that dynamically learns kernel eigenvalues and output coefficients simultaneously during training. Unlike fixed-kernel methods tied to the neural tangent kernel theory, the diagonal adaptive kernel model adapts to the structure of the truth function, significantly improving generalization over fixed-kernel methods, especially when the initial kernel is misaligned with the target. Moreover, we show that the adaptivity comes from learning the right eigenvalues during training, showing a feature learning behavior. By extending to deeper parameterization, we further show how extra depth enhances adaptability and generalization. This study combines the insights from feature learning and implicit regularization and provides new perspective into the adaptivity and generalization potential of neural networks beyond the kernel regime.
Towards a Statistical Understanding of Neural Networks: Beyond the Neural Tangent Kernel Theories
Dec 25, 2024Abstract:A primary advantage of neural networks lies in their feature learning characteristics, which is challenging to theoretically analyze due to the complexity of their training dynamics. We propose a new paradigm for studying feature learning and the resulting benefits in generalizability. After reviewing the neural tangent kernel (NTK) theory and recent results in kernel regression, which address the generalization issue of sufficiently wide neural networks, we examine limitations and implications of the fixed kernel theory (as the NTK theory) and review recent theoretical advancements in feature learning. Moving beyond the fixed kernel/feature theory, we consider neural networks as adaptive feature models. Finally, we propose an over-parameterized Gaussian sequence model as a prototype model to study the feature learning characteristics of neural networks.
Optimizing Instruction Synthesis: Effective Exploration of Evolutionary Space with Tree Search
Oct 14, 2024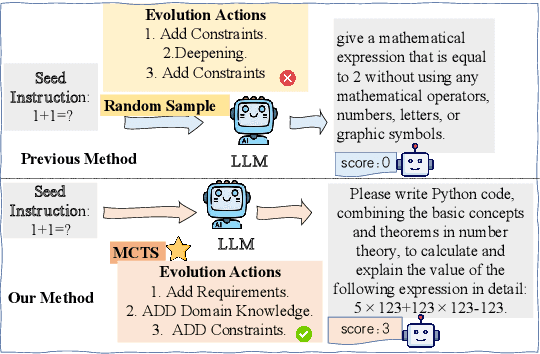
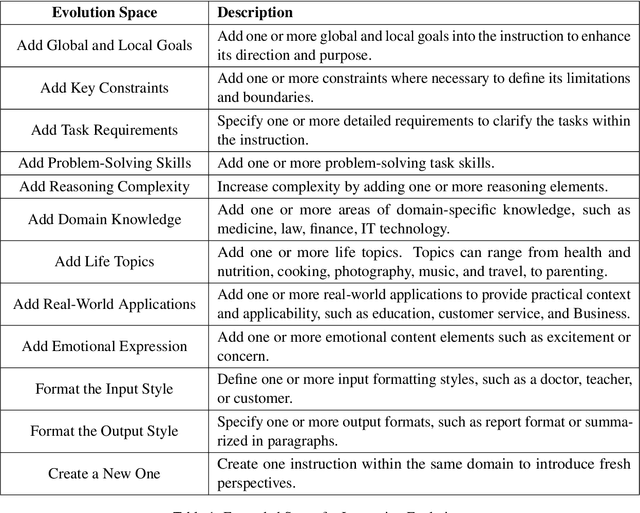

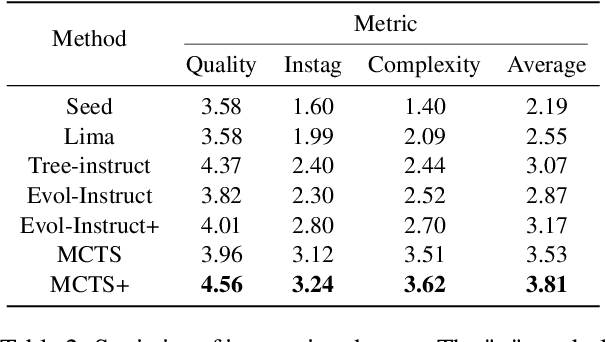
Abstract:Instruction tuning is a crucial technique for aligning language models with humans' actual goals in the real world. Extensive research has highlighted the quality of instruction data is essential for the success of this alignment. However, creating high-quality data manually is labor-intensive and time-consuming, which leads researchers to explore using LLMs to synthesize data. Recent studies have focused on using a stronger LLM to iteratively enhance existing instruction data, showing promising results. Nevertheless, previous work often lacks control over the evolution direction, resulting in high uncertainty in the data synthesis process and low-quality instructions. In this paper, we introduce a general and scalable framework, IDEA-MCTS (Instruction Data Enhancement using Monte Carlo Tree Search), a scalable framework for efficiently synthesizing instructions. With tree search and evaluation models, it can efficiently guide each instruction to evolve into a high-quality form, aiding in instruction fine-tuning. Experimental results show that IDEA-MCTS significantly enhances the seed instruction data, raising the average evaluation scores of quality, diversity, and complexity from 2.19 to 3.81. Furthermore, in open-domain benchmarks, experimental results show that IDEA-MCTS improves the accuracy of real-world instruction-following skills in LLMs by an average of 5\% in low-resource settings.
On the Impacts of the Random Initialization in the Neural Tangent Kernel Theory
Oct 08, 2024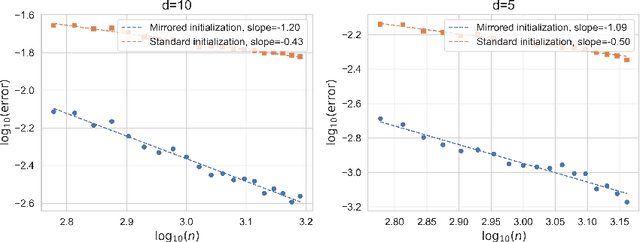


Abstract:This paper aims to discuss the impact of random initialization of neural networks in the neural tangent kernel (NTK) theory, which is ignored by most recent works in the NTK theory. It is well known that as the network's width tends to infinity, the neural network with random initialization converges to a Gaussian process $f^{\mathrm{GP}}$, which takes values in $L^{2}(\mathcal{X})$, where $\mathcal{X}$ is the domain of the data. In contrast, to adopt the traditional theory of kernel regression, most recent works introduced a special mirrored architecture and a mirrored (random) initialization to ensure the network's output is identically zero at initialization. Therefore, it remains a question whether the conventional setting and mirrored initialization would make wide neural networks exhibit different generalization capabilities. In this paper, we first show that the training dynamics of the gradient flow of neural networks with random initialization converge uniformly to that of the corresponding NTK regression with random initialization $f^{\mathrm{GP}}$. We then show that $\mathbf{P}(f^{\mathrm{GP}} \in [\mathcal{H}^{\mathrm{NT}}]^{s}) = 1$ for any $s < \frac{3}{d+1}$ and $\mathbf{P}(f^{\mathrm{GP}} \in [\mathcal{H}^{\mathrm{NT}}]^{s}) = 0$ for any $s \geq \frac{3}{d+1}$, where $[\mathcal{H}^{\mathrm{NT}}]^{s}$ is the real interpolation space of the RKHS $\mathcal{H}^{\mathrm{NT}}$ associated with the NTK. Consequently, the generalization error of the wide neural network trained by gradient descent is $\Omega(n^{-\frac{3}{d+3}})$, and it still suffers from the curse of dimensionality. On one hand, the result highlights the benefits of mirror initialization. On the other hand, it implies that NTK theory may not fully explain the superior performance of neural networks.
Improving Adaptivity via Over-Parameterization in Sequence Models
Sep 02, 2024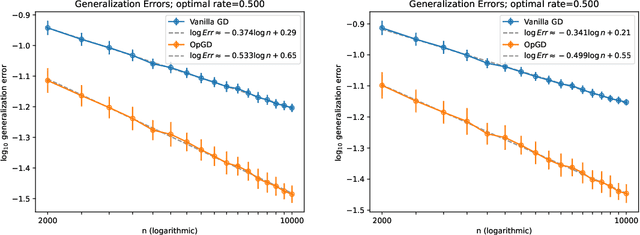

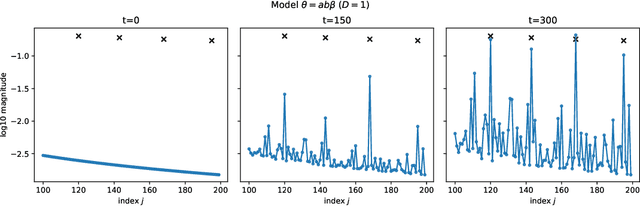

Abstract:It is well known that eigenfunctions of a kernel play a crucial role in kernel regression. Through several examples, we demonstrate that even with the same set of eigenfunctions, the order of these functions significantly impacts regression outcomes. Simplifying the model by diagonalizing the kernel, we introduce an over-parameterized gradient descent in the realm of sequence model to capture the effects of various orders of a fixed set of eigen-functions. This method is designed to explore the impact of varying eigenfunction orders. Our theoretical results show that the over-parameterization gradient flow can adapt to the underlying structure of the signal and significantly outperform the vanilla gradient flow method. Moreover, we also demonstrate that deeper over-parameterization can further enhance the generalization capability of the model. These results not only provide a new perspective on the benefits of over-parameterization and but also offer insights into the adaptivity and generalization potential of neural networks beyond the kernel regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge