Qian Lin
Several Supporting Evidences for the Adaptive Feature Program
Nov 12, 2025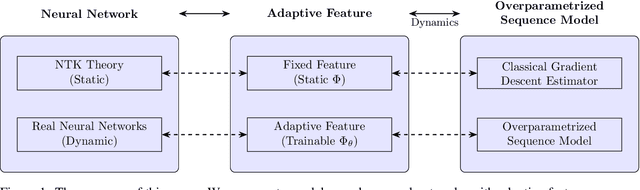
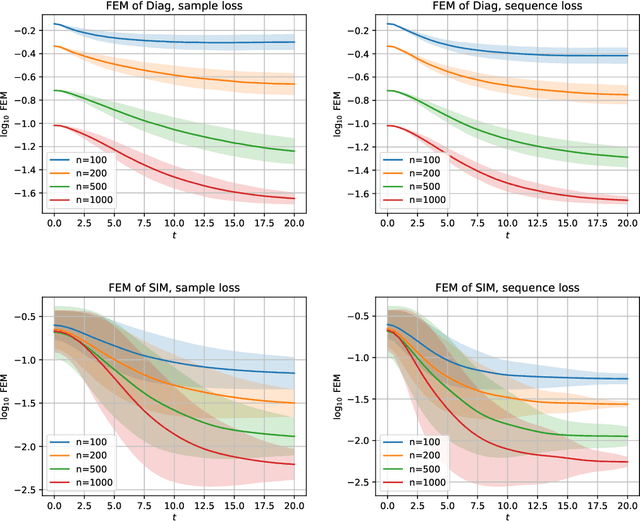
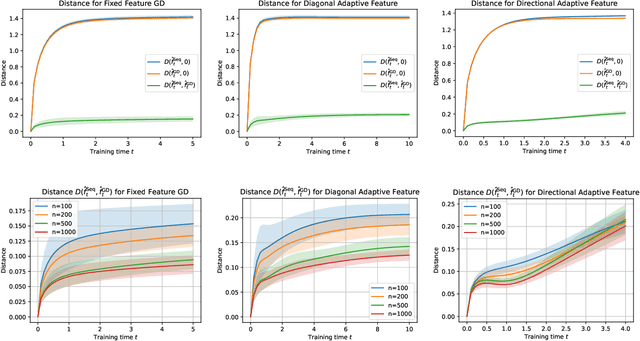
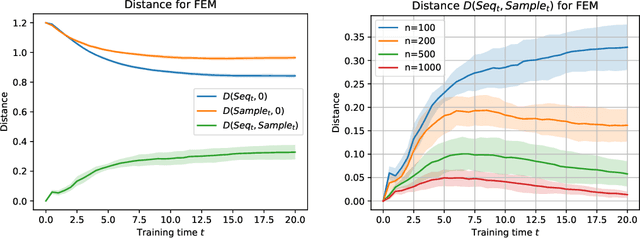
Abstract:Theoretically exploring the advantages of neural networks might be one of the most challenging problems in the AI era. An adaptive feature program has recently been proposed to analyze the feature learning characteristic property of neural networks in a more abstract way. Motivated by the celebrated Le Cam equivalence, we advocate the over-parametrized sequence models to further simplify the analysis of the training dynamics of adaptive feature program and present several supporting evidences for the adaptive feature program. More precisely, after having introduced the feature error measure (FEM) to characterize the quality of the learned feature, we show that the FEM is decreasing during the training process of several concrete adaptive feature models including linear regression, single/multiple index models, etc. We believe that this hints at the potential successes of the adaptive feature program.
Reg3D: Reconstructive Geometry Instruction Tuning for 3D Scene Understanding
Sep 03, 2025Abstract:The rapid development of Large Multimodal Models (LMMs) has led to remarkable progress in 2D visual understanding; however, extending these capabilities to 3D scene understanding remains a significant challenge. Existing approaches predominantly rely on text-only supervision, which fails to provide the geometric constraints required for learning robust 3D spatial representations. In this paper, we introduce Reg3D, a novel Reconstructive Geometry Instruction Tuning framework that addresses this limitation by incorporating geometry-aware supervision directly into the training process. Our key insight is that effective 3D understanding necessitates reconstructing underlying geometric structures rather than merely describing them. Unlike existing methods that inject 3D information solely at the input level, Reg3D adopts a dual-supervision paradigm that leverages 3D geometric information both as input and as explicit learning targets. Specifically, we design complementary object-level and frame-level reconstruction tasks within a dual-encoder architecture, enforcing geometric consistency to encourage the development of spatial reasoning capabilities. Extensive experiments on ScanQA, Scan2Cap, ScanRefer, and SQA3D demonstrate that Reg3D delivers substantial performance improvements, establishing a new training paradigm for spatially aware multimodal models.
Neural Tangent Kernel of Neural Networks with Loss Informed by Differential Operators
Mar 14, 2025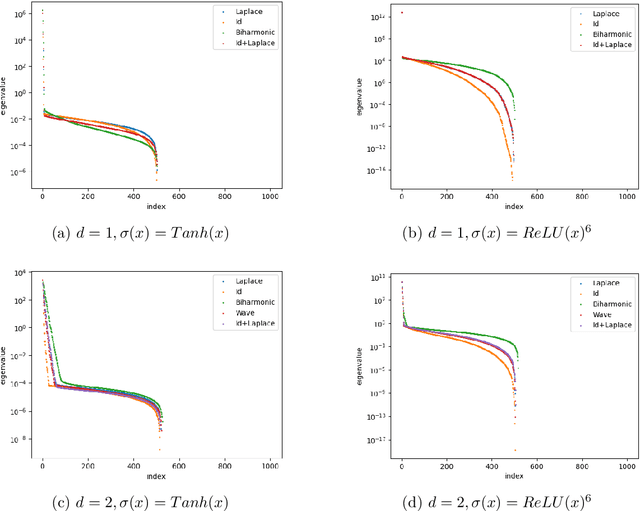

Abstract:Spectral bias is a significant phenomenon in neural network training and can be explained by neural tangent kernel (NTK) theory. In this work, we develop the NTK theory for deep neural networks with physics-informed loss, providing insights into the convergence of NTK during initialization and training, and revealing its explicit structure. We find that, in most cases, the differential operators in the loss function do not induce a faster eigenvalue decay rate and stronger spectral bias. Some experimental results are also presented to verify the theory.
Diagonal Over-parameterization in Reproducing Kernel Hilbert Spaces as an Adaptive Feature Model: Generalization and Adaptivity
Jan 15, 2025

Abstract:This paper introduces a diagonal adaptive kernel model that dynamically learns kernel eigenvalues and output coefficients simultaneously during training. Unlike fixed-kernel methods tied to the neural tangent kernel theory, the diagonal adaptive kernel model adapts to the structure of the truth function, significantly improving generalization over fixed-kernel methods, especially when the initial kernel is misaligned with the target. Moreover, we show that the adaptivity comes from learning the right eigenvalues during training, showing a feature learning behavior. By extending to deeper parameterization, we further show how extra depth enhances adaptability and generalization. This study combines the insights from feature learning and implicit regularization and provides new perspective into the adaptivity and generalization potential of neural networks beyond the kernel regime.
Towards a Statistical Understanding of Neural Networks: Beyond the Neural Tangent Kernel Theories
Dec 25, 2024Abstract:A primary advantage of neural networks lies in their feature learning characteristics, which is challenging to theoretically analyze due to the complexity of their training dynamics. We propose a new paradigm for studying feature learning and the resulting benefits in generalizability. After reviewing the neural tangent kernel (NTK) theory and recent results in kernel regression, which address the generalization issue of sufficiently wide neural networks, we examine limitations and implications of the fixed kernel theory (as the NTK theory) and review recent theoretical advancements in feature learning. Moving beyond the fixed kernel/feature theory, we consider neural networks as adaptive feature models. Finally, we propose an over-parameterized Gaussian sequence model as a prototype model to study the feature learning characteristics of neural networks.
On the Impacts of the Random Initialization in the Neural Tangent Kernel Theory
Oct 08, 2024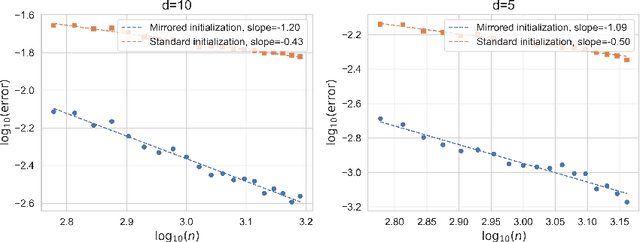


Abstract:This paper aims to discuss the impact of random initialization of neural networks in the neural tangent kernel (NTK) theory, which is ignored by most recent works in the NTK theory. It is well known that as the network's width tends to infinity, the neural network with random initialization converges to a Gaussian process $f^{\mathrm{GP}}$, which takes values in $L^{2}(\mathcal{X})$, where $\mathcal{X}$ is the domain of the data. In contrast, to adopt the traditional theory of kernel regression, most recent works introduced a special mirrored architecture and a mirrored (random) initialization to ensure the network's output is identically zero at initialization. Therefore, it remains a question whether the conventional setting and mirrored initialization would make wide neural networks exhibit different generalization capabilities. In this paper, we first show that the training dynamics of the gradient flow of neural networks with random initialization converge uniformly to that of the corresponding NTK regression with random initialization $f^{\mathrm{GP}}$. We then show that $\mathbf{P}(f^{\mathrm{GP}} \in [\mathcal{H}^{\mathrm{NT}}]^{s}) = 1$ for any $s < \frac{3}{d+1}$ and $\mathbf{P}(f^{\mathrm{GP}} \in [\mathcal{H}^{\mathrm{NT}}]^{s}) = 0$ for any $s \geq \frac{3}{d+1}$, where $[\mathcal{H}^{\mathrm{NT}}]^{s}$ is the real interpolation space of the RKHS $\mathcal{H}^{\mathrm{NT}}$ associated with the NTK. Consequently, the generalization error of the wide neural network trained by gradient descent is $\Omega(n^{-\frac{3}{d+3}})$, and it still suffers from the curse of dimensionality. On one hand, the result highlights the benefits of mirror initialization. On the other hand, it implies that NTK theory may not fully explain the superior performance of neural networks.
An Offline Adaptation Framework for Constrained Multi-Objective Reinforcement Learning
Sep 16, 2024Abstract:In recent years, significant progress has been made in multi-objective reinforcement learning (RL) research, which aims to balance multiple objectives by incorporating preferences for each objective. In most existing studies, specific preferences must be provided during deployment to indicate the desired policies explicitly. However, designing these preferences depends heavily on human prior knowledge, which is typically obtained through extensive observation of high-performing demonstrations with expected behaviors. In this work, we propose a simple yet effective offline adaptation framework for multi-objective RL problems without assuming handcrafted target preferences, but only given several demonstrations to implicitly indicate the preferences of expected policies. Additionally, we demonstrate that our framework can naturally be extended to meet constraints on safety-critical objectives by utilizing safe demonstrations, even when the safety thresholds are unknown. Empirical results on offline multi-objective and safe tasks demonstrate the capability of our framework to infer policies that align with real preferences while meeting the constraints implied by the provided demonstrations.
Improving Adaptivity via Over-Parameterization in Sequence Models
Sep 02, 2024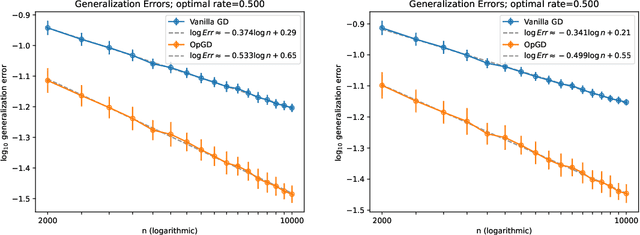

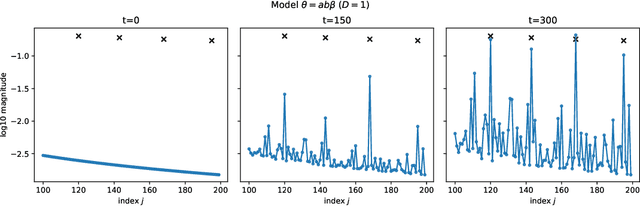

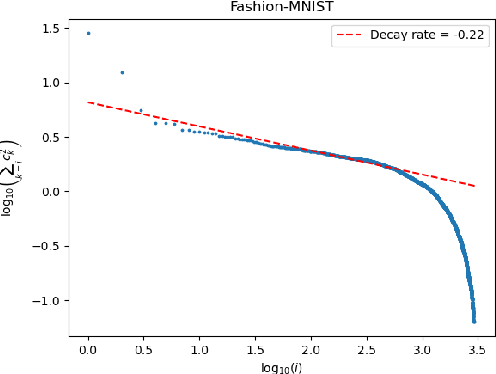
Abstract:It is well known that eigenfunctions of a kernel play a crucial role in kernel regression. Through several examples, we demonstrate that even with the same set of eigenfunctions, the order of these functions significantly impacts regression outcomes. Simplifying the model by diagonalizing the kernel, we introduce an over-parameterized gradient descent in the realm of sequence model to capture the effects of various orders of a fixed set of eigen-functions. This method is designed to explore the impact of varying eigenfunction orders. Our theoretical results show that the over-parameterization gradient flow can adapt to the underlying structure of the signal and significantly outperform the vanilla gradient flow method. Moreover, we also demonstrate that deeper over-parameterization can further enhance the generalization capability of the model. These results not only provide a new perspective on the benefits of over-parameterization and but also offer insights into the adaptivity and generalization potential of neural networks beyond the kernel regime.
On the Pinsker bound of inner product kernel regression in large dimensions
Sep 02, 2024

Abstract:Building on recent studies of large-dimensional kernel regression, particularly those involving inner product kernels on the sphere $\mathbb{S}^{d}$, we investigate the Pinsker bound for inner product kernel regression in such settings. Specifically, we address the scenario where the sample size $n$ is given by $\alpha d^{\gamma}(1+o_{d}(1))$ for some $\alpha, \gamma>0$. We have determined the exact minimax risk for kernel regression in this setting, not only identifying the minimax rate but also the exact constant, known as the Pinsker constant, associated with the excess risk.
On the Saturation Effect of Kernel Ridge Regression
May 15, 2024



Abstract:The saturation effect refers to the phenomenon that the kernel ridge regression (KRR) fails to achieve the information theoretical lower bound when the smoothness of the underground truth function exceeds certain level. The saturation effect has been widely observed in practices and a saturation lower bound of KRR has been conjectured for decades. In this paper, we provide a proof of this long-standing conjecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge