ForgetMark: Stealthy Fingerprint Embedding via Targeted Unlearning in Language Models

Existing invasive (backdoor) fingerprints suffer from high-perplexity triggers that are easily filtered, fixed response patterns exposed by heuristic detectors, and spurious activations on benign inputs. We introduce \textsc{ForgetMark}, a stealthy fingerprinting framework that encodes provenance via targeted unlearning. It builds a compact, human-readable key--value set with an assistant model and predictive-entropy ranking, then trains lightweight LoRA adapters to suppress the original values on their keys while preserving general capabilities. Ownership is verified under black/gray-box access by aggregating likelihood and semantic evidence into a fingerprint success rate. By relying on probabilistic forgetting traces rather than fixed trigger--response patterns, \textsc{ForgetMark} avoids high-perplexity triggers, reduces detectability, and lowers false triggers. Across diverse architectures and settings, it achieves 100\% ownership verification on fingerprinted models while maintaining standard performance, surpasses backdoor baselines in stealthiness and robustness to model merging, and remains effective under moderate incremental fine-tuning. Our code and data are available at \href{https://github.com/Xuzhenhua55/ForgetMark}{https://github.com/Xuzhenhua55/ForgetMark}.

Chain-of-Generation: Progressive Latent Diffusion for Text-Guided Molecular Design

Text-conditioned molecular generation aims to translate natural-language descriptions into chemical structures, enabling scientists to specify functional groups, scaffolds, and physicochemical constraints without handcrafted rules. Diffusion-based models, particularly latent diffusion models (LDMs), have recently shown promise by performing stochastic search in a continuous latent space that compactly captures molecular semantics. Yet existing methods rely on one-shot conditioning, where the entire prompt is encoded once and applied throughout diffusion, making it hard to satisfy all the requirements in the prompt. We discuss three outstanding challenges of one-shot conditioning generation, including the poor interpretability of the generated components, the failure to generate all substructures, and the overambition in considering all requirements simultaneously. We then propose three principles to address those challenges, motivated by which we propose Chain-of-Generation (CoG), a training-free multi-stage latent diffusion framework. CoG decomposes each prompt into curriculum-ordered semantic segments and progressively incorporates them as intermediate goals, guiding the denoising trajectory toward molecules that satisfy increasingly rich linguistic constraints. To reinforce semantic guidance, we further introduce a post-alignment learning phase that strengthens the correspondence between textual and molecular latent spaces. Extensive experiments on benchmark and real-world tasks demonstrate that CoG yields higher semantic alignment, diversity, and controllability than one-shot baselines, producing molecules that more faithfully reflect complex, compositional prompts while offering transparent insight into the generation process.

The FM Agent

Large language models (LLMs) are catalyzing the development of autonomous AI research agents for scientific and engineering discovery. We present FM Agent, a novel and general-purpose multi-agent framework that leverages a synergistic combination of LLM-based reasoning and large-scale evolutionary search to address complex real-world challenges. The core of FM Agent integrates several key innovations: 1) a cold-start initialization phase incorporating expert guidance, 2) a novel evolutionary sampling strategy for iterative optimization, 3) domain-specific evaluators that combine correctness, effectiveness, and LLM-supervised feedback, and 4) a distributed, asynchronous execution infrastructure built on Ray. Demonstrating broad applicability, our system has been evaluated across diverse domains, including operations research, machine learning, GPU kernel optimization, and classical mathematical problems. FM Agent reaches state-of-the-art results autonomously, without human interpretation or tuning -- 1976.3 on ALE-Bench (+5.2\%), 43.56\% on MLE-Bench (+4.0pp), up to 20x speedups on KernelBench, and establishes new state-of-the-art(SOTA) results on several classical mathematical problems. Beyond academic benchmarks, FM Agent shows considerable promise for both large-scale enterprise R\&D workflows and fundamental scientific research, where it can accelerate innovation, automate complex discovery processes, and deliver substantial engineering and scientific advances with broader societal impact.

Unraveling LoRA Interference: Orthogonal Subspaces for Robust Model Merging

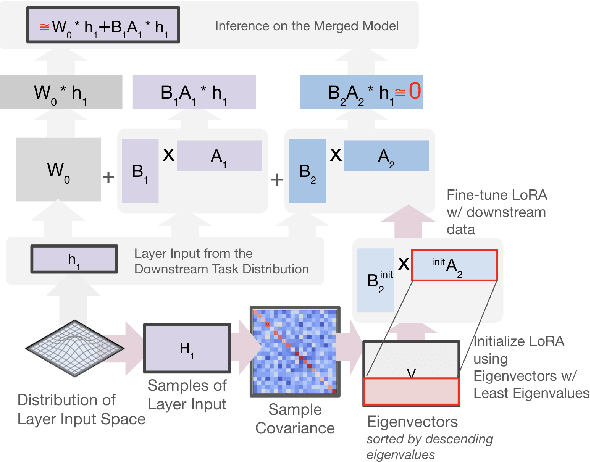
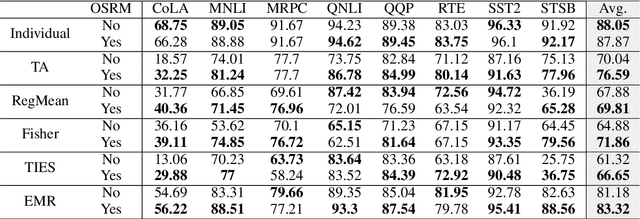
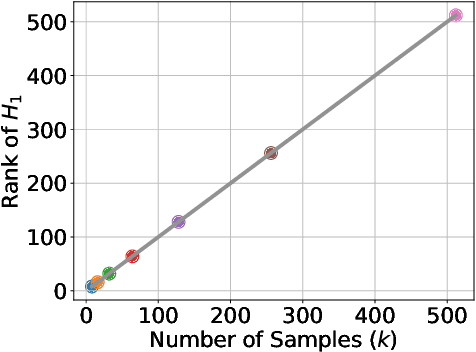
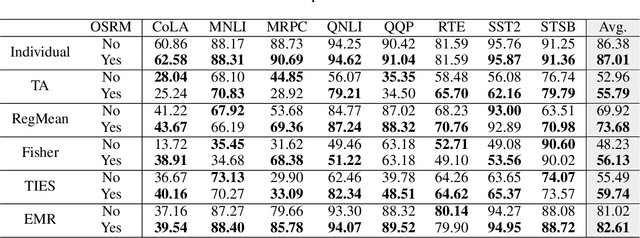
Fine-tuning large language models (LMs) for individual tasks yields strong performance but is expensive for deployment and storage. Recent works explore model merging to combine multiple task-specific models into a single multi-task model without additional training. However, existing merging methods often fail for models fine-tuned with low-rank adaptation (LoRA), due to significant performance degradation. In this paper, we show that this issue arises from a previously overlooked interplay between model parameters and data distributions. We propose Orthogonal Subspaces for Robust model Merging (OSRM) to constrain the LoRA subspace *prior* to fine-tuning, ensuring that updates relevant to one task do not adversely shift outputs for others. Our approach can seamlessly integrate with most existing merging algorithms, reducing the unintended interference among tasks. Extensive experiments on eight datasets, tested with three widely used LMs and two large LMs, demonstrate that our method not only boosts merging performance but also preserves single-task accuracy. Furthermore, our approach exhibits greater robustness to the hyperparameters of merging. These results highlight the importance of data-parameter interaction in model merging and offer a plug-and-play solution for merging LoRA models.

Towards a Statistical Understanding of Neural Networks: Beyond the Neural Tangent Kernel Theories

A primary advantage of neural networks lies in their feature learning characteristics, which is challenging to theoretically analyze due to the complexity of their training dynamics. We propose a new paradigm for studying feature learning and the resulting benefits in generalizability. After reviewing the neural tangent kernel (NTK) theory and recent results in kernel regression, which address the generalization issue of sufficiently wide neural networks, we examine limitations and implications of the fixed kernel theory (as the NTK theory) and review recent theoretical advancements in feature learning. Moving beyond the fixed kernel/feature theory, we consider neural networks as adaptive feature models. Finally, we propose an over-parameterized Gaussian sequence model as a prototype model to study the feature learning characteristics of neural networks.

On the Pinsker bound of inner product kernel regression in large dimensions

Building on recent studies of large-dimensional kernel regression, particularly those involving inner product kernels on the sphere $\mathbb{S}^{d}$, we investigate the Pinsker bound for inner product kernel regression in such settings. Specifically, we address the scenario where the sample size $n$ is given by $\alpha d^{\gamma}(1+o_{d}(1))$ for some $\alpha, \gamma>0$. We have determined the exact minimax risk for kernel regression in this setting, not only identifying the minimax rate but also the exact constant, known as the Pinsker constant, associated with the excess risk.

On the Saturation Effect of Kernel Ridge Regression

The saturation effect refers to the phenomenon that the kernel ridge regression (KRR) fails to achieve the information theoretical lower bound when the smoothness of the underground truth function exceeds certain level. The saturation effect has been widely observed in practices and a saturation lower bound of KRR has been conjectured for decades. In this paper, we provide a proof of this long-standing conjecture.

The phase diagram of kernel interpolation in large dimensions

The generalization ability of kernel interpolation in large dimensions (i.e., $n \asymp d^{\gamma}$ for some $\gamma>0$) might be one of the most interesting problems in the recent renaissance of kernel regression, since it may help us understand the 'benign overfitting phenomenon' reported in the neural networks literature. Focusing on the inner product kernel on the sphere, we fully characterized the exact order of both the variance and bias of large-dimensional kernel interpolation under various source conditions $s\geq 0$. Consequently, we obtained the $(s,\gamma)$-phase diagram of large-dimensional kernel interpolation, i.e., we determined the regions in $(s,\gamma)$-plane where the kernel interpolation is minimax optimal, sub-optimal and inconsistent.

Multi-target Detection for Reconfigurable Holographic Surfaces Enabled Radar

Multi-target detection is one of the primary tasks in radar-based localization and sensing, typically built on phased array antennas. However, the bulky hardware in the phased array restricts its potential for enhancing detection accuracy, since the cost and power of the phased array can become unaffordable as its physical aperture scales up to pursue higher beam shaping capabilities. To resolve this issue, we propose a radar system enabled by reconfigurable holographic surfaces (RHSs), a novel meta-surface antenna composed of meta-material elements with cost-effective and power-efficient hardware, which performs multi-target detection in an adaptive manner. Different from the phase-control structure in the phased array, the RHS is able to apply beamforming by controlling the radiation amplitudes of its elements. Consequently, traditional beamforming schemes designed for phased arrays cannot be directly applied to RHSs due to this structural difference. To tackle this challenge, a waveform and amplitude optimization algorithm (WAOA) is designed to jointly optimize the radar waveform and RHS amplitudes in order to improve the detection accuracy. Simulation results reveal that the proposed RHS-enabled radar increases the probability of detection by 0.13 compared to phased array radars when six iterations of adaptive detection are performed given the same hardware cost.

Reconfigurable Holographic Surface Aided Wireless Simultaneous Localization and Mapping

As a crucial facilitator of future autonomous driving applications, wireless simultaneous localization and mapping (SLAM) has drawn growing attention recently. However, the accuracy of existing wireless SLAM schemes is limited because the antenna gain is constrained given the cost budget due to the expensive hardware components such as phase arrays. To address this issue, we propose a reconfigurable holographic surface (RHS)-aided SLAM system in this paper. The RHS is a novel type of low-cost antenna that can cut down the hardware cost by replacing phased arrays in conventional SLAM systems. However, compared with a phased array where the phase shifts of parallelfed signals are adjusted, the RHS exhibits a different radiation model because its amplitude-controlled radiation elements are series-fed by surface waves, implying that traditional schemes cannot be applied directly. To address this challenge, we propose an RHS-aided beam steering method for sensing the surrounding environment and design the corresponding SLAM algorithm. Simulation results show that the proposed scheme can achieve more than there times the localization accuracy that traditional wireless SLAM with the same cost achieves.