Towards a Statistical Understanding of Neural Networks: Beyond the Neural Tangent Kernel Theories

A primary advantage of neural networks lies in their feature learning characteristics, which is challenging to theoretically analyze due to the complexity of their training dynamics. We propose a new paradigm for studying feature learning and the resulting benefits in generalizability. After reviewing the neural tangent kernel (NTK) theory and recent results in kernel regression, which address the generalization issue of sufficiently wide neural networks, we examine limitations and implications of the fixed kernel theory (as the NTK theory) and review recent theoretical advancements in feature learning. Moving beyond the fixed kernel/feature theory, we consider neural networks as adaptive feature models. Finally, we propose an over-parameterized Gaussian sequence model as a prototype model to study the feature learning characteristics of neural networks.

The Optimality of Kernel Classifiers in Sobolev Space

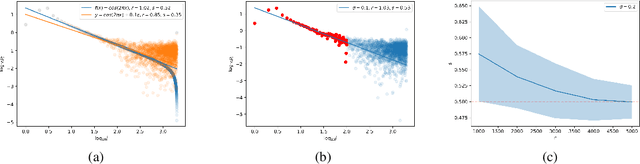
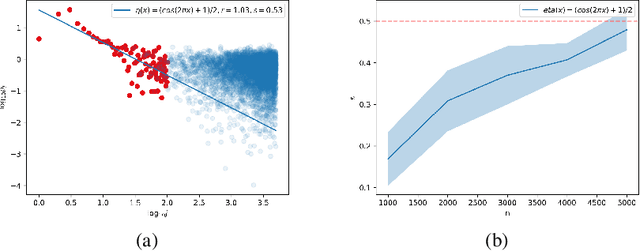
Kernel methods are widely used in machine learning, especially for classification problems. However, the theoretical analysis of kernel classification is still limited. This paper investigates the statistical performances of kernel classifiers. With some mild assumptions on the conditional probability $\eta(x)=\mathbb{P}(Y=1\mid X=x)$, we derive an upper bound on the classification excess risk of a kernel classifier using recent advances in the theory of kernel regression. We also obtain a minimax lower bound for Sobolev spaces, which shows the optimality of the proposed classifier. Our theoretical results can be extended to the generalization error of overparameterized neural network classifiers. To make our theoretical results more applicable in realistic settings, we also propose a simple method to estimate the interpolation smoothness of $2\eta(x)-1$ and apply the method to real datasets.

Generalization Ability of Wide Residual Networks

In this paper, we study the generalization ability of the wide residual network on $\mathbb{S}^{d-1}$ with the ReLU activation function. We first show that as the width $m\rightarrow\infty$, the residual network kernel (RNK) uniformly converges to the residual neural tangent kernel (RNTK). This uniform convergence further guarantees that the generalization error of the residual network converges to that of the kernel regression with respect to the RNTK. As direct corollaries, we then show $i)$ the wide residual network with the early stopping strategy can achieve the minimax rate provided that the target regression function falls in the reproducing kernel Hilbert space (RKHS) associated with the RNTK; $ii)$ the wide residual network can not generalize well if it is trained till overfitting the data. We finally illustrate some experiments to reconcile the contradiction between our theoretical result and the widely observed ``benign overfitting phenomenon''

Generalization Ability of Wide Neural Networks on $\mathbb{R}$

We perform a study on the generalization ability of the wide two-layer ReLU neural network on $\mathbb{R}$. We first establish some spectral properties of the neural tangent kernel (NTK): $a)$ $K_{d}$, the NTK defined on $\mathbb{R}^{d}$, is positive definite; $b)$ $\lambda_{i}(K_{1})$, the $i$-th largest eigenvalue of $K_{1}$, is proportional to $i^{-2}$. We then show that: $i)$ when the width $m\rightarrow\infty$, the neural network kernel (NNK) uniformly converges to the NTK; $ii)$ the minimax rate of regression over the RKHS associated to $K_{1}$ is $n^{-2/3}$; $iii)$ if one adopts the early stopping strategy in training a wide neural network, the resulting neural network achieves the minimax rate; $iv)$ if one trains the neural network till it overfits the data, the resulting neural network can not generalize well. Finally, we provide an explanation to reconcile our theory and the widely observed ``benign overfitting phenomenon''.