Multi-scale Feature Fusion with Point Pyramid for 3D Object Detection

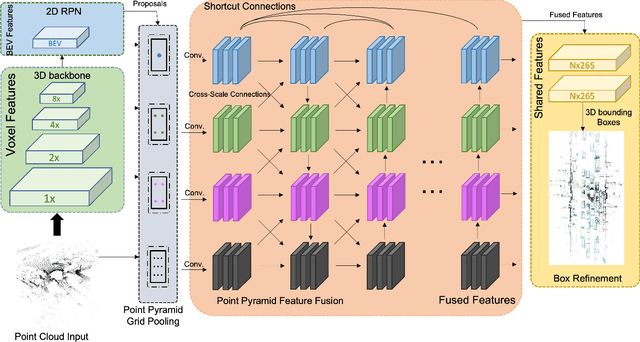
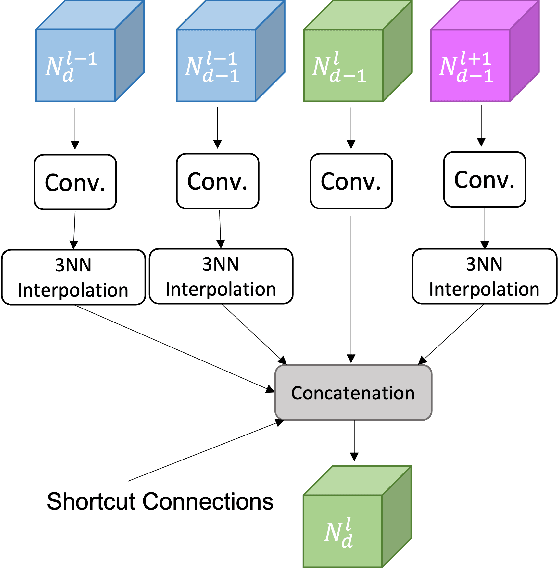
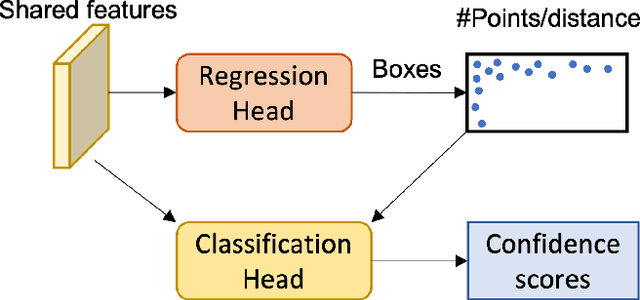
Effective point cloud processing is crucial to LiDARbased autonomous driving systems. The capability to understand features at multiple scales is required for object detection of intelligent vehicles, where road users may appear in different sizes. Recent methods focus on the design of the feature aggregation operators, which collect features at different scales from the encoder backbone and assign them to the points of interest. While efforts are made into the aggregation modules, the importance of how to fuse these multi-scale features has been overlooked. This leads to insufficient feature communication across scales. To address this issue, this paper proposes the Point Pyramid RCNN (POP-RCNN), a feature pyramid-based framework for 3D object detection on point clouds. POP-RCNN consists of a Point Pyramid Feature Enhancement (PPFE) module to establish connections across spatial scales and semantic depths for information exchange. The PPFE module effectively fuses multi-scale features for rich information without the increased complexity in feature aggregation. To remedy the impact of inconsistent point densities, a point density confidence module is deployed. This design integration enables the use of a lightweight feature aggregator, and the emphasis on both shallow and deep semantics, realising a detection framework for 3D object detection. With great adaptability, the proposed method can be applied to a variety of existing frameworks to increase feature richness, especially for long-distance detection. By adopting the PPFE in the voxel-based and point-voxel-based baselines, experimental results on KITTI and Waymo Open Dataset show that the proposed method achieves remarkable performance even with limited computational headroom.

On the Pinsker bound of inner product kernel regression in large dimensions

Building on recent studies of large-dimensional kernel regression, particularly those involving inner product kernels on the sphere $\mathbb{S}^{d}$, we investigate the Pinsker bound for inner product kernel regression in such settings. Specifically, we address the scenario where the sample size $n$ is given by $\alpha d^{\gamma}(1+o_{d}(1))$ for some $\alpha, \gamma>0$. We have determined the exact minimax risk for kernel regression in this setting, not only identifying the minimax rate but also the exact constant, known as the Pinsker constant, associated with the excess risk.

The phase diagram of kernel interpolation in large dimensions

The generalization ability of kernel interpolation in large dimensions (i.e., $n \asymp d^{\gamma}$ for some $\gamma>0$) might be one of the most interesting problems in the recent renaissance of kernel regression, since it may help us understand the 'benign overfitting phenomenon' reported in the neural networks literature. Focusing on the inner product kernel on the sphere, we fully characterized the exact order of both the variance and bias of large-dimensional kernel interpolation under various source conditions $s\geq 0$. Consequently, we obtained the $(s,\gamma)$-phase diagram of large-dimensional kernel interpolation, i.e., we determined the regions in $(s,\gamma)$-plane where the kernel interpolation is minimax optimal, sub-optimal and inconsistent.

Optimal Rates of Kernel Ridge Regression under Source Condition in Large Dimensions

Motivated by the studies of neural networks (e.g.,the neural tangent kernel theory), we perform a study on the large-dimensional behavior of kernel ridge regression (KRR) where the sample size $n \asymp d^{\gamma}$ for some $\gamma > 0$. Given an RKHS $\mathcal{H}$ associated with an inner product kernel defined on the sphere $\mathbb{S}^{d}$, we suppose that the true function $f_{\rho}^{*} \in [\mathcal{H}]^{s}$, the interpolation space of $\mathcal{H}$ with source condition $s>0$. We first determined the exact order (both upper and lower bound) of the generalization error of kernel ridge regression for the optimally chosen regularization parameter $\lambda$. We then further showed that when $0<s\le1$, KRR is minimax optimal; and when $s>1$, KRR is not minimax optimal (a.k.a. he saturation effect). Our results illustrate that the curves of rate varying along $\gamma$ exhibit the periodic plateau behavior and the multiple descent behavior and show how the curves evolve with $s>0$. Interestingly, our work provides a unified viewpoint of several recent works on kernel regression in the large-dimensional setting, which correspond to $s=0$ and $s=1$ respectively.

Optimal Rate of Kernel Regression in Large Dimensions

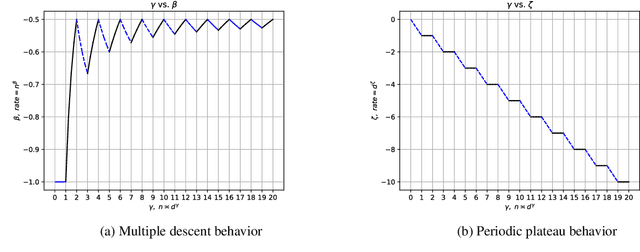
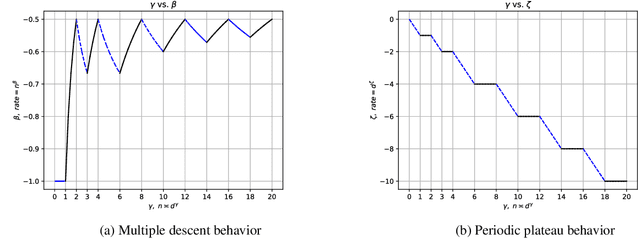
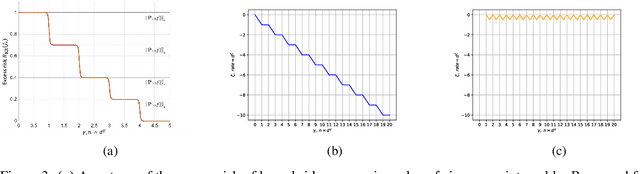
We perform a study on kernel regression for large-dimensional data (where the sample size $n$ is polynomially depending on the dimension $d$ of the samples, i.e., $n\asymp d^{\gamma}$ for some $\gamma >0$ ). We first build a general tool to characterize the upper bound and the minimax lower bound of kernel regression for large dimensional data through the Mendelson complexity $\varepsilon_{n}^{2}$ and the metric entropy $\bar{\varepsilon}_{n}^{2}$ respectively. When the target function falls into the RKHS associated with a (general) inner product model defined on $\mathbb{S}^{d}$, we utilize the new tool to show that the minimax rate of the excess risk of kernel regression is $n^{-1/2}$ when $n\asymp d^{\gamma}$ for $\gamma =2, 4, 6, 8, \cdots$. We then further determine the optimal rate of the excess risk of kernel regression for all the $\gamma>0$ and find that the curve of optimal rate varying along $\gamma$ exhibits several new phenomena including the {\it multiple descent behavior} and the {\it periodic plateau behavior}. As an application, For the neural tangent kernel (NTK), we also provide a similar explicit description of the curve of optimal rate. As a direct corollary, we know these claims hold for wide neural networks as well.

On the Optimality of Misspecified Kernel Ridge Regression

In the misspecified kernel ridge regression problem, researchers usually assume the underground true function $f_{\rho}^{*} \in [\mathcal{H}]^{s}$, a less-smooth interpolation space of a reproducing kernel Hilbert space (RKHS) $\mathcal{H}$ for some $s\in (0,1)$. The existing minimax optimal results require $\|f_{\rho}^{*}\|_{L^{\infty}}<\infty$ which implicitly requires $s > \alpha_{0}$ where $\alpha_{0}\in (0,1)$ is the embedding index, a constant depending on $\mathcal{H}$. Whether the KRR is optimal for all $s\in (0,1)$ is an outstanding problem lasting for years. In this paper, we show that KRR is minimax optimal for any $s\in (0,1)$ when the $\mathcal{H}$ is a Sobolev RKHS.