Divergence of Empirical Neural Tangent Kernel in Classification Problems

This paper demonstrates that in classification problems, fully connected neural networks (FCNs) and residual neural networks (ResNets) cannot be approximated by kernel logistic regression based on the Neural Tangent Kernel (NTK) under overtraining (i.e., when training time approaches infinity). Specifically, when using the cross-entropy loss, regardless of how large the network width is (as long as it is finite), the empirical NTK diverges from the NTK on the training samples as training time increases. To establish this result, we first demonstrate the strictly positive definiteness of the NTKs for multi-layer FCNs and ResNets. Then, we prove that during training, % with the cross-entropy loss, the neural network parameters diverge if the smallest eigenvalue of the empirical NTK matrix (Gram matrix) with respect to training samples is bounded below by a positive constant. This behavior contrasts sharply with the lazy training regime commonly observed in regression problems. Consequently, using a proof by contradiction, we show that the empirical NTK does not uniformly converge to the NTK across all times on the training samples as the network width increases. We validate our theoretical results through experiments on both synthetic data and the MNIST classification task. This finding implies that NTK theory is not applicable in this context, with significant theoretical implications for understanding neural networks in classification problems.

On the Impacts of the Random Initialization in the Neural Tangent Kernel Theory

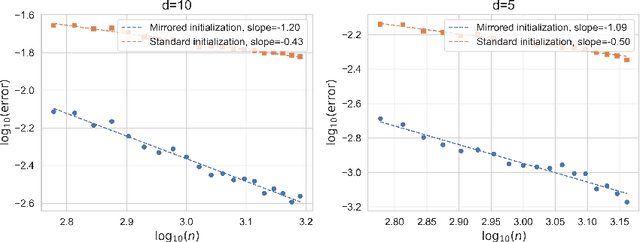
This paper aims to discuss the impact of random initialization of neural networks in the neural tangent kernel (NTK) theory, which is ignored by most recent works in the NTK theory. It is well known that as the network's width tends to infinity, the neural network with random initialization converges to a Gaussian process $f^{\mathrm{GP}}$, which takes values in $L^{2}(\mathcal{X})$, where $\mathcal{X}$ is the domain of the data. In contrast, to adopt the traditional theory of kernel regression, most recent works introduced a special mirrored architecture and a mirrored (random) initialization to ensure the network's output is identically zero at initialization. Therefore, it remains a question whether the conventional setting and mirrored initialization would make wide neural networks exhibit different generalization capabilities. In this paper, we first show that the training dynamics of the gradient flow of neural networks with random initialization converge uniformly to that of the corresponding NTK regression with random initialization $f^{\mathrm{GP}}$. We then show that $\mathbf{P}(f^{\mathrm{GP}} \in [\mathcal{H}^{\mathrm{NT}}]^{s}) = 1$ for any $s < \frac{3}{d+1}$ and $\mathbf{P}(f^{\mathrm{GP}} \in [\mathcal{H}^{\mathrm{NT}}]^{s}) = 0$ for any $s \geq \frac{3}{d+1}$, where $[\mathcal{H}^{\mathrm{NT}}]^{s}$ is the real interpolation space of the RKHS $\mathcal{H}^{\mathrm{NT}}$ associated with the NTK. Consequently, the generalization error of the wide neural network trained by gradient descent is $\Omega(n^{-\frac{3}{d+3}})$, and it still suffers from the curse of dimensionality. On one hand, the result highlights the benefits of mirror initialization. On the other hand, it implies that NTK theory may not fully explain the superior performance of neural networks.

Statistical Optimality of Deep Wide Neural Networks

In this paper, we consider the generalization ability of deep wide feedforward ReLU neural networks defined on a bounded domain $\mathcal X \subset \mathbb R^{d}$. We first demonstrate that the generalization ability of the neural network can be fully characterized by that of the corresponding deep neural tangent kernel (NTK) regression. We then investigate on the spectral properties of the deep NTK and show that the deep NTK is positive definite on $\mathcal{X}$ and its eigenvalue decay rate is $(d+1)/d$. Thanks to the well established theories in kernel regression, we then conclude that multilayer wide neural networks trained by gradient descent with proper early stopping achieve the minimax rate, provided that the regression function lies in the reproducing kernel Hilbert space (RKHS) associated with the corresponding NTK. Finally, we illustrate that the overfitted multilayer wide neural networks can not generalize well on $\mathbb S^{d}$.