Zuoqiang Shi
BlinDNO: A Distributional Neural Operator for Dynamical System Reconstruction from Time-Label-Free data
Nov 15, 2025Abstract:We study an inverse problem for stochastic and quantum dynamical systems in a time-label-free setting, where only unordered density snapshots sampled at unknown times drawn from an observation-time distribution are available. These observations induce a distribution over state densities, from which we seek to recover the parameters of the underlying evolution operator. We formulate this as learning a distribution-to-function neural operator and propose BlinDNO, a permutation-invariant architecture that integrates a multiscale U-Net encoder with an attention-based mixer. Numerical experiments on a wide range of stochastic and quantum systems, including a 3D protein-folding mechanism reconstruction problem in a cryo-EM setting, demonstrate that BlinDNO reliably recovers governing parameters and consistently outperforms existing neural inverse operator baselines.
In vivo 3D ultrasound computed tomography of musculoskeletal tissues with generative neural physics
Aug 17, 2025Abstract:Ultrasound computed tomography (USCT) is a radiation-free, high-resolution modality but remains limited for musculoskeletal imaging due to conventional ray-based reconstructions that neglect strong scattering. We propose a generative neural physics framework that couples generative networks with physics-informed neural simulation for fast, high-fidelity 3D USCT. By learning a compact surrogate of ultrasonic wave propagation from only dozens of cross-modality images, our method merges the accuracy of wave modeling with the efficiency and stability of deep learning. This enables accurate quantitative imaging of in vivo musculoskeletal tissues, producing spatial maps of acoustic properties beyond reflection-mode images. On synthetic and in vivo data (breast, arm, leg), we reconstruct 3D maps of tissue parameters in under ten minutes, with sensitivity to biomechanical properties in muscle and bone and resolution comparable to MRI. By overcoming computational bottlenecks in strongly scattering regimes, this approach advances USCT toward routine clinical assessment of musculoskeletal disease.
Neural Tangent Kernel of Neural Networks with Loss Informed by Differential Operators
Mar 14, 2025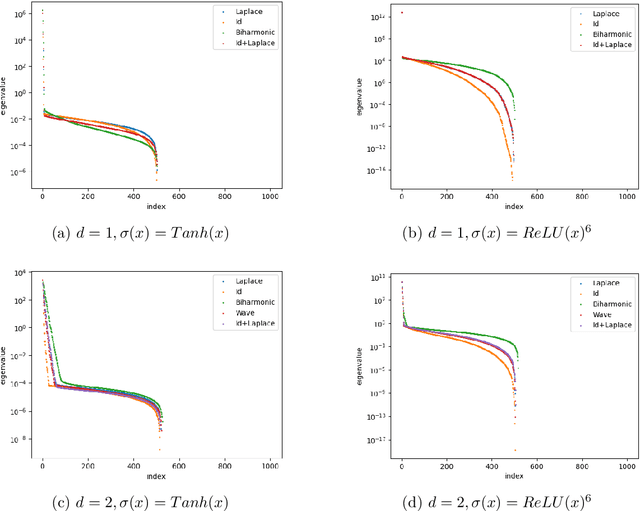

Abstract:Spectral bias is a significant phenomenon in neural network training and can be explained by neural tangent kernel (NTK) theory. In this work, we develop the NTK theory for deep neural networks with physics-informed loss, providing insights into the convergence of NTK during initialization and training, and revealing its explicit structure. We find that, in most cases, the differential operators in the loss function do not induce a faster eigenvalue decay rate and stronger spectral bias. Some experimental results are also presented to verify the theory.
Neumann Series-based Neural Operator for Solving Inverse Medium Problem
Sep 14, 2024


Abstract:The inverse medium problem, inherently ill-posed and nonlinear, presents significant computational challenges. This study introduces a novel approach by integrating a Neumann series structure within a neural network framework to effectively handle multiparameter inputs. Experiments demonstrate that our methodology not only accelerates computations but also significantly enhances generalization performance, even with varying scattering properties and noisy data. The robustness and adaptability of our framework provide crucial insights and methodologies, extending its applicability to a broad spectrum of scattering problems. These advancements mark a significant step forward in the field, offering a scalable solution to traditionally complex inverse problems.
Fast and Scalable Semi-Supervised Learning for Multi-View Subspace Clustering
Aug 11, 2024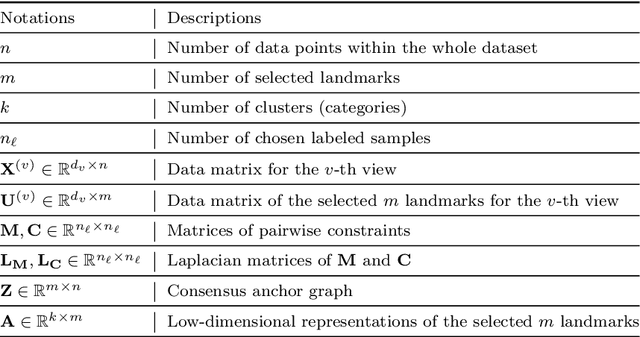
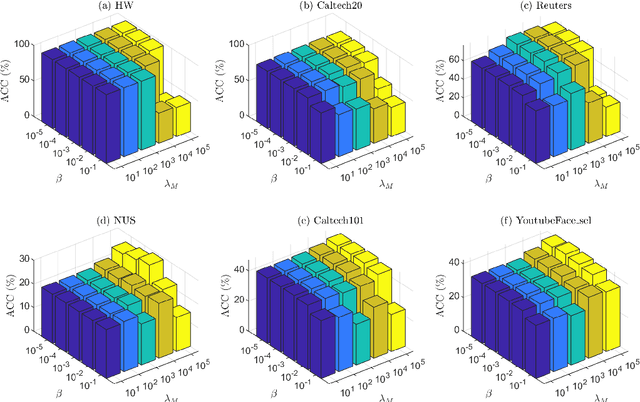
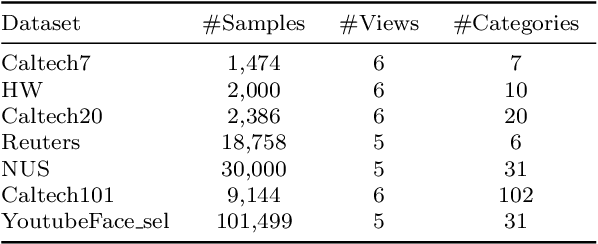
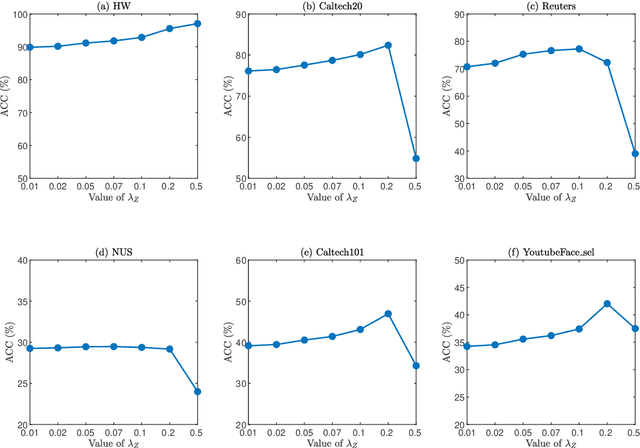
Abstract:In this paper, we introduce a Fast and Scalable Semi-supervised Multi-view Subspace Clustering (FSSMSC) method, a novel solution to the high computational complexity commonly found in existing approaches. FSSMSC features linear computational and space complexity relative to the size of the data. The method generates a consensus anchor graph across all views, representing each data point as a sparse linear combination of chosen landmarks. Unlike traditional methods that manage the anchor graph construction and the label propagation process separately, this paper proposes a unified optimization model that facilitates simultaneous learning of both. An effective alternating update algorithm with convergence guarantees is proposed to solve the unified optimization model. Additionally, the method employs the obtained anchor graph and landmarks' low-dimensional representations to deduce low-dimensional representations for raw data. Following this, a straightforward clustering approach is conducted on these low-dimensional representations to achieve the final clustering results. The effectiveness and efficiency of FSSMSC are validated through extensive experiments on multiple benchmark datasets of varying scales.
Deep Learning with Data Privacy via Residual Perturbation
Aug 11, 2024Abstract:Protecting data privacy in deep learning (DL) is of crucial importance. Several celebrated privacy notions have been established and used for privacy-preserving DL. However, many existing mechanisms achieve privacy at the cost of significant utility degradation and computational overhead. In this paper, we propose a stochastic differential equation-based residual perturbation for privacy-preserving DL, which injects Gaussian noise into each residual mapping of ResNets. Theoretically, we prove that residual perturbation guarantees differential privacy (DP) and reduces the generalization gap of DL. Empirically, we show that residual perturbation is computationally efficient and outperforms the state-of-the-art differentially private stochastic gradient descent (DPSGD) in utility maintenance without sacrificing membership privacy.
Interface Laplace Learning: Learnable Interface Term Helps Semi-Supervised Learning
Aug 10, 2024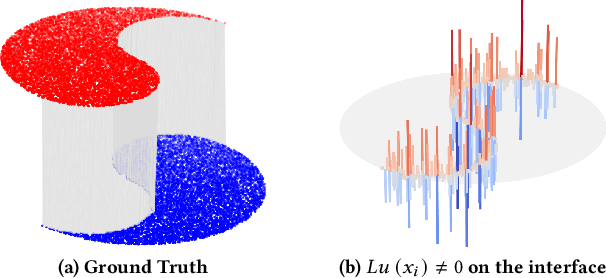
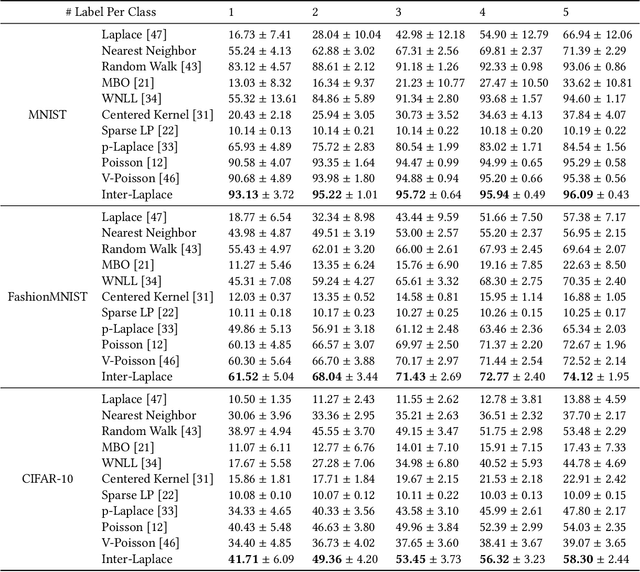
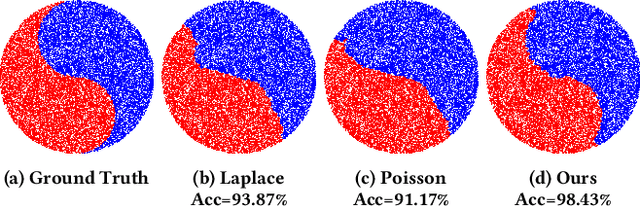
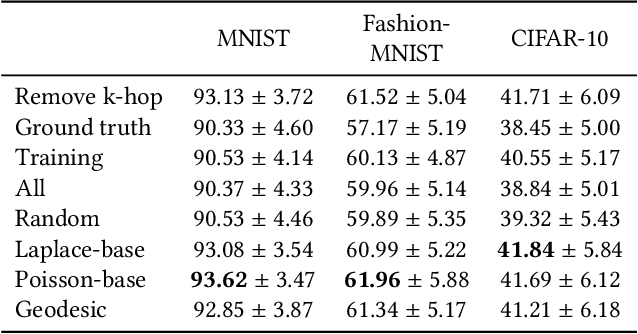
Abstract:We introduce a novel framework, called Interface Laplace learning, for graph-based semi-supervised learning. Motivated by the observation that an interface should exist between different classes where the function value is non-smooth, we introduce a Laplace learning model that incorporates an interface term. This model challenges the long-standing assumption that functions are smooth at all unlabeled points. In the proposed approach, we add an interface term to the Laplace learning model at the interface positions. We provide a practical algorithm to approximate the interface positions using k-hop neighborhood indices, and to learn the interface term from labeled data without artificial design. Our method is efficient and effective, and we present extensive experiments demonstrating that Interface Laplace learning achieves better performance than other recent semi-supervised learning approaches at extremely low label rates on the MNIST, FashionMNIST, and CIFAR-10 datasets.
Convection-Diffusion Equation: A Theoretically Certified Framework for Neural Networks
Mar 23, 2024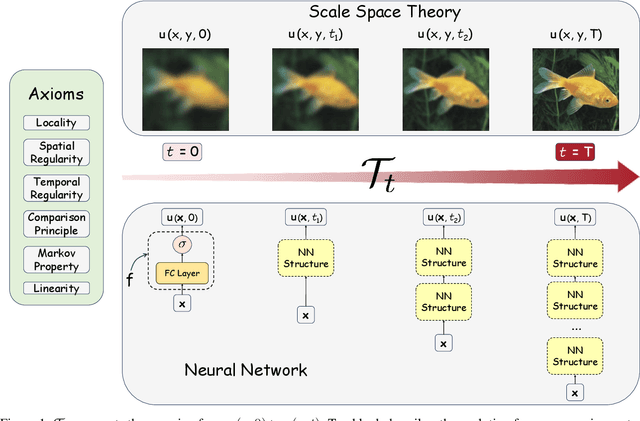
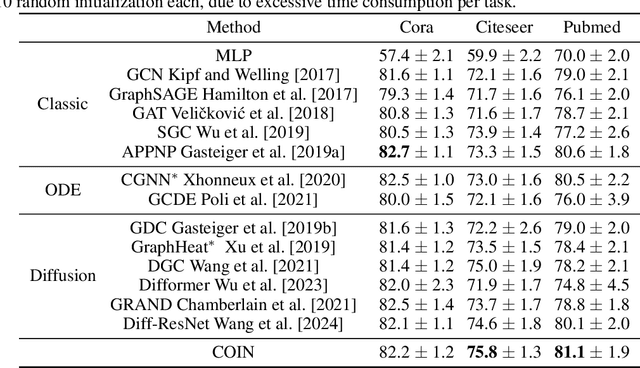

Abstract:In this paper, we study the partial differential equation models of neural networks. Neural network can be viewed as a map from a simple base model to a complicate function. Based on solid analysis, we show that this map can be formulated by a convection-diffusion equation. This theoretically certified framework gives mathematical foundation and more understanding of neural networks. Moreover, based on the convection-diffusion equation model, we design a novel network structure, which incorporates diffusion mechanism into network architecture. Extensive experiments on both benchmark datasets and real-world applications validate the performance of the proposed model.
Generalization Error Curves for Analytic Spectral Algorithms under Power-law Decay
Jan 03, 2024Abstract:The generalization error curve of certain kernel regression method aims at determining the exact order of generalization error with various source condition, noise level and choice of the regularization parameter rather than the minimax rate. In this work, under mild assumptions, we rigorously provide a full characterization of the generalization error curves of the kernel gradient descent method (and a large class of analytic spectral algorithms) in kernel regression. Consequently, we could sharpen the near inconsistency of kernel interpolation and clarify the saturation effects of kernel regression algorithms with higher qualification, etc. Thanks to the neural tangent kernel theory, these results greatly improve our understanding of the generalization behavior of training the wide neural networks. A novel technical contribution, the analytic functional argument, might be of independent interest.
Neural Born Series Operator for Biomedical Ultrasound Computed Tomography
Dec 25, 2023Abstract:Ultrasound Computed Tomography (USCT) provides a radiation-free option for high-resolution clinical imaging. Despite its potential, the computationally intensive Full Waveform Inversion (FWI) required for tissue property reconstruction limits its clinical utility. This paper introduces the Neural Born Series Operator (NBSO), a novel technique designed to speed up wave simulations, thereby facilitating a more efficient USCT image reconstruction process through an NBSO-based FWI pipeline. Thoroughly validated on comprehensive brain and breast datasets, simulated under experimental USCT conditions, the NBSO proves to be accurate and efficient in both forward simulation and image reconstruction. This advancement demonstrates the potential of neural operators in facilitating near real-time USCT reconstruction, making the clinical application of USCT increasingly viable and promising.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge